这种 F 类配置通过在其
晶体管的电压波形中添加三次谐波分量来提高输出功率和效率。但是,我们花在如何生成这个三次谐波分量上的时间相对较少。
在本文中,我们将更详细地研究该
放大器的原理图。然后,我们将推导出具有平坦波形的三次谐波峰值放大器的设计方程。在这种情况下,“平坦”意味着集电极电压的导数在其峰值和谷值处为零。针对平坦波形进行设计简化了所涉及的数学分析,同时仍然提供了我们在实际 F 类放大器中观察到的波形的良好近似值。

图 1 显示了三次谐波尖峰 F 类放大器的电路原理图。
三次谐波峰值 F 类放大器的电路原理图。
图 1.三次谐波峰值 F 类放大器的电路原理图。
在上述电路中,输入偏置是晶体管的导通电压。因此,集电极电流是半波整流正弦波,就像 B 类放大器一样。与 B 类放大器不同,晶体管作为
开关工作。该电路本身实际上与 B 类电路非常相似,只是增加了一个谐振电路 (L3和 C3) 调谐到三次谐波。
L 的并联组合3和 C3近似于三次谐波处的开路,但在远离三次谐波的频率上充当短路。同样,基谐谐振器(由 L0和 C0) 在基频处充当开路,并在其他谐波频率处将 output node 短接至地。我们可以将负载网络的行为总结如下:
在基频下, L3和 C3连接起短路和 L0和 C0连接近似于开路。负载网络的阻抗为RL到晶体管。
在三次泛音处,L3和 C3连接充当开路。因此,负载网络向晶体管提供开路。
在其他谐波频率(4 次、5 次等)下,两个谐振电路都起短路的作用。负载网络对晶体管的阻抗实际上是短路。
由于 L0-C0tank 电路与RL并且除基频分量外的所有组件短路,则输出电压是基频处的正弦波形。L 上出现三次谐波电压3-C3谐振器,因为它对输出电流具有高阻抗。
请注意,集电极电压是负载电压与 L 两端电压之和3-C3tank 电路。这样,L3-C3Resonator 在集电极电压上增加了一个三次谐波分量。
平坦的 F 类波形
正如我们在上一篇文章中学到的,三次谐波尖化 F 类放大器的集电极电压波形可以表示为:
$$\begin{eqnarray}v_{F} ~&=&~ V_{cc} ~-~A_1 \sin(\omega t)~-~A_3 \sin(3 \omega t) \\~&=&~V_{cc} ~-~A_1 \Big (\sin(\omega t)~+x~ ~\times~ \sin(3 \omega t) \Big )\end{eqnarray}$$
方程 1.
哪里:
一个1= 基波电压分量的幅度
一个3= 三次谐波分量的振幅
x = 一个3/一个1.
图 2 也摘自上一篇文章,说明了如何vF如果我们合并不同级别的 Third-Harmonic 分量,则会发生变化。
具有不同 A3/A1 值的 F 类集电极电压波形。
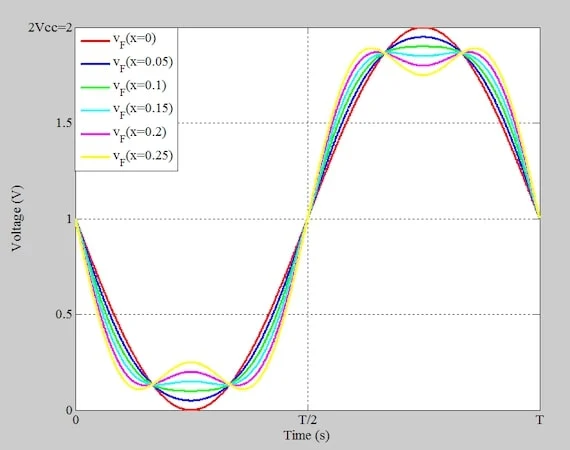
图 2.A 的 F 类集电极电压 1 = V抄送 = 1 V,x 值 从 0 到 0.25 不等。
当我们将 x 从 0 增加到大约 0.1 时,总电压在其波峰和波谷附近变得更平坦。但是,当 x 超过 0.1 时,波形中会出现一些波纹。在本文中,我们将通过设计尽可能平坦的波形来简化操作。
虽然我们将绕过详细的推导过程,但设计过程的步是确定集电极电压波形的和限制 (vF来自公式 1)。我们通过差异化来实现这一目标vF从等式 1 中将结果设为零。
接下来,我们计算vF并在限制处将其设置为零。这将在 A1和 A3.终结果是,对于平坦的波形,我们应该有:
$$A_3 ~=~ \frac{1}{9} A_1$$
方程 2.
通过组合公式 1 和 2,我们得到平坦的集电极电压:
$$v_{F} ~=~ V_{cc} ~-~A_1 \big ( \sin(\omega t)~+~ \frac{1}{9} \sin(3 \omega t) \big )$$
方程 3.
图 3 中的绿色曲线vF对于 A1 = V抄送= 1 V 和 A3= 0.11,对应于 x = 1/9。包括正弦红色曲线 (x = 0),以便我们可以更清楚地看到波形的平坦化。
F 类集电极电压,A1 = Vcc = 1 V 和 x = 1/9。
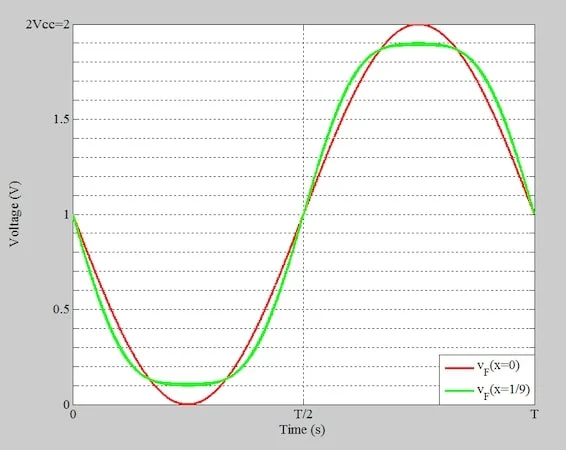
图 3.A 的 F 类集电极电压 1 = V抄送 = 1 V 且 x = 1/9。
在上图中,很明显,可用的摆动 (0 到 2V抄送,在本例中为 0 至 2 V)未得到充分利用。我们可以增加基波元件的输入功率,以充分利用电位摆动。为此,我们注意到vF出现在 ?t = π/2 处。将值等于 0 V,我们得到:
$$V_{cc}~-~A_1(1~-~\frac{1}{9})~=~0 \quad \rightarrow \quad A_1~=~\frac{9}{8}V_{cc}$$
方程 4.
插入 A 的这个值1到公式 3 中,我们得到了全电压摆幅的平坦电压波形:
$$v_{F} ~=~ V_{cc}~-~ \frac{9}{8} \sin(\omega t) ~-~\frac{1}{8} \sin(3 \omega t)$$
方程 5.
计算 F 类放大器的效率
正如上一篇文章不止地指出的那样,甚至在结束语中,F 类放大器代表了比 B 类放大器的效率更高的提高。让我们在本节中对此进行测试。
与往常一样,放大器的理论效率等于平均负载功率除以从
电源汲取的功率 (\(\eta~=~\frac{P_L}{P_{cc}}\))。使用基波电压分量的幅度(公式 4),我们可以计算PL如下:
$$P_L~=~ \frac{v_{o, rms}^2}{R_L}~=~ \frac{1}{2}\frac{ A_1^2}{R_L} \quad \rightarrow \quad P_L ~=~ \frac{81}{128} ~\times~ \frac{V_{cc}^2}{R_L}$$
方程 6.
这比 B 类操作高出约 27%。
我们通过找到集电极电流的平均值并将其乘以电源电压 (V抄送).导通角为 180 度(π 弧度),我们可以假设集电极电流是振幅的半波整流正弦波我p和周期 T(图 4)。
集电极电流是半波整流正弦波。
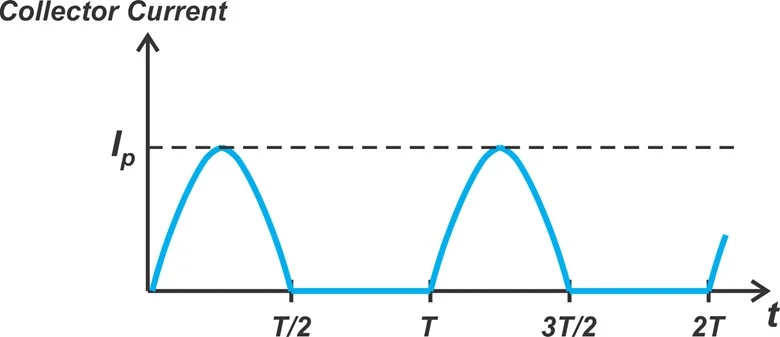
图 4.集电极电流是半波整流正弦波。
请注意,虽然 F 类放大器的导通角在大多数应用中通常设置为 180 度,但它可以是小于 180 度的任何值。
使用傅里叶级数表示,我们用集电极电流的组成频率分量来表示集电极电流:
$$i_{collector}(t)~=~ \frac{I_p}{\pi} ~+~ \frac{I_p}{2}\sin(\omega_0 t) ~-~ \frac{2I_p}{3\pi} \cos(2 \omega_0t)~-~ \frac{2I_p}{15\pi} \cos(4 \omega_0t) ~+~ ...$$
方程 7.
从公式 7 中可以看出,图 4 中半波整流信号的平均值为我p/π.因此,电源提供的功率为:
$$P_{cc}~=~\frac{I_p V_{cc}}{\pi}$$
方程 8.
公式 6 和 8 分别给出了放大器的负载功率和电源功率。然而,在我们使用公式 8 计算放大器的效率之前,我们需要在我p和V抄送.
基波分量的振幅为我p/2.该电流流入负载 (RL) 并产生 A 的基波电压幅度1= (9/8)V抄送.因此,我们获得:
$$\frac{I_p}{2} ~\times~ R_L ~=~\frac{9}{8} V_{cc} \quad \rightarrow \quad I_p ~=~ \frac{9}{4}\frac{V_{cc}}{R_L}$$
方程 9.
结合方程 8 和 9,我们找到一个新的关系P抄送:
$$P_{cc}~=~\frac{I_p V_{cc}}{\pi}~=~\frac{9}{4 \pi} ~\times~ \frac{V_{cc}^2}{ R_L}$$
方程 10.
,使用公式 6 和 10,我们可以计算 F 类放大器的效率:
$$\eta ~=~ \frac{P_L}{P_{cc}} ~=~ \frac{\frac{81}{128} ~\times~ \frac{V_{cc}^2}{R_L}}{\frac{9}{4 \pi} ~\times~ \frac{V_{cc}^2}{ R_L}}~=~\frac{9 \pi}{32}~=~88.4 \ \%$$
方程 11.
相比之下,B 类放大器的效率为:
$$\eta_{max} ~=~ \frac{\pi}{4}~=~78.5 \, \%$$
方程 12.
三次谐波峰值 F 类放大器将效率提高了 \(\frac{9}{8}\) 或 1.125。
示例:设计三次谐波峰值 F 类放大器
让我们用一个设计示例来结束本文。对于向 50 Ω 负载提供 50 W W 的三次谐波峰值 F 类放大器,确定以下内容:
所需的电源电压 (V抄送).
电流 (我p) 和电压 (2V抄送) 的 Transistor 必须容忍的 Transistor 必须承受的 Lam S 的 S S T
基频谐振器的元件值 (L0和 C0在图 1 中)。
假设载波频率 (fc) 为 500 MHz,所需带宽 (BW) 为 75 MHz。
公式 6 显示了具有三次谐波峰化的 F 类级向负载提供的功率。代PL= 50 W 和RL= 50 Ω,我们得到:
$$50 ~=~ \frac{81}{128} ~\times~ \frac{V_{cc}^2}{50} ~~\rightarrow~~ V_{cc}~=~ 62.85 \ \text{V}$$
方程 13.
所需的电源电压为 62.85 V。这使得晶体管两端的电压为 125.7 V,因为它等于 2V抄送.根据公式 9,流经晶体管的电流为:
$$I_p ~=~ \frac{9}{4}\frac{V_{cc}}{R_L} ~=~ \frac{9}{4} ~\times~ \frac{62.85}{50}~=~2.83 \ \text{A}$$
方程 14.
现在剩下的就是找到所需的
电感 (L0) 和电容 (C0) 的 Tim S为此,我们首先需要找到负载 Q 因子。使用给定的载波频率 (fc= 500 MHz) 和带宽 (BW = 75 MHz) 值,我们可以按如下方式计算 Q 因子:
$$Q_L ~=~ \frac{f_c}{BW}~=~\frac{500}{75}~=~6.67$$
方程 15.
对于并联调谐的 RLC 电路,Q 因子与元件值的关系如下:
$$Q_L ~=~ \frac{R_L}{L \omega_c}~=~{R_L C \omega_c}$$
方程 16.
因为QL= 6.67 和RL= 50 Ω,则 L 的值0锻炼可以:
$$L_0 ~=~ \frac{R_L}{\omega_c Q_L}~=~\frac{50}{2 \pi ~\times~ 500 ~\times~ 10^6 ~\times~ 6.67}~=~2.4 \ \text{nH}$$
方程 17.
,所需的电容为:
$$C_0 ~=~ \frac{Q_L}{\omega_c R_L}~=~\frac{6.67}{2 \pi ~\times~ 500 ~\times~ 10^6 ~\times~ 50}~=~42.46 \ \text{pF}$$
方程 18.
结语
B 级的效率为 78.5%。相比之下,具有平坦波形的三次谐波峰值放大器的效率为 88.4%。我们将在下一篇文章中讨论一种更高效、更不平坦的三次谐波峰值放大器。



