在电子系统中,模拟 - 数字转换器(ADC)扮演着至关重要的角色,它能够将连续的模拟信号转换为离散的数字信号。下面我们将详细分析几种常见的 ADC 转换过程。
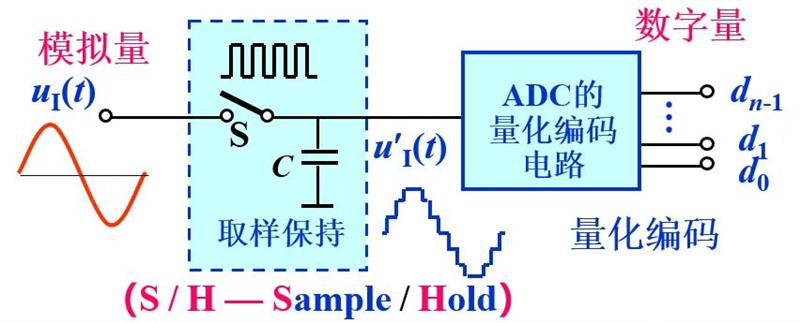
- 转换步骤
- 取样:这是将时间连续变化的信号转变为时间离散信号的过程。在实际应用中,通过周期性地对模拟信号进行采样,获取特定时刻的信号值,从而实现信号在时间上的离散化。
- 保持:对取样得到的信号进行保持,确保有足够的时间将其转换为数字信号。这一步骤对于后续的量化和编码过程非常关键,保证了信号的稳定性。
- 量化和编码:量化单位是数字信号位 LSB 所对应的模拟信号大小,用Δ表示。量化就是把取样后的保持信号化为量化单位的整数倍。由于模拟电压不一定能被Δ整除,会产生量化误差。编码则是将量化后的数值用二进制代码表示。划分量化电平有两种常见方法,一种是只舍不入法,另一种是有舍有入法。只舍不入法是将小于量化单位的部分舍去,而有舍有入法是根据小于或大于量化单位一半的情况进行舍入处理,有舍有入法的量化误差相对较小。
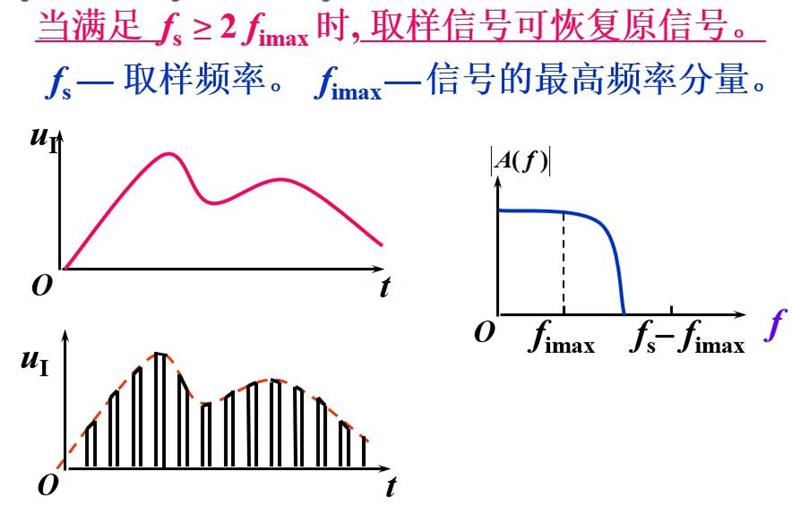
- 取样定理
取样定理指出,为了能够准确地恢复原始模拟信号,取样频率必须至少是模拟信号频率的两倍。这一定理为 ADC 的设计和应用提供了重要的理论依据,确保了信号转换的准确性。
在取样 - 保持电路中,当控制信号uL为高电平时,开关管T导通,电容Ch充电,输出电压uO等于输入电压uI,即uO=uI=uC。当uL为低电平时,T截止,电容Ch基本不放电,uO保持。然而,这里存在一个矛盾:为了使电容Ch充电速度快,输入电阻Ri越小越好;但为了使电路具有高输入电阻,Ri越大越好。为了解决这个问题,出现了改进电路,如 LF198。LF198 通过引入缓冲放大器等措施,既保证了快速充电,又提高了电路的输入电阻。其工作原理是利用缓冲放大器的高输入阻抗和低输出阻抗特性,将输入信号和电容充电过程隔离开来,从而优化了电路性能。

- 基本工作原理
逐次渐近型 A/D 转换器通过逐次比较的方式来确定数字输出。它从位开始,依次确定每一位的数值。在每比较中,将输入模拟信号与一个由内部 DAC 产生的参考电压进行比较,如果输入信号大于参考电压,则该位为 1;否则为 0。通过多次比较,逐步逼近输入模拟信号的数值。 - 转换过程举例
假设我们有一个 4 位的逐次渐近型 A/D 转换器,输入模拟电压为Vin。首先,将位(MSB)置为 1,由 DAC 产生对应的参考电压Vref,并与Vin进行比较。如果Vin≥Vref,则位保持为 1;否则置为 0。然后,依次对次高位、第三位和位进行同样的比较操作,终得到 4 位的数字输出。
- 电路组成和工作原理
双积分型 A/D 转换器主要由积分器、比较器、计数器和控制逻辑等部分组成。其工作过程分为两个阶段:阶段是对输入模拟信号进行固定时间的积分,积分时间为T1;第二阶段是对一个已知的参考电压进行反向积分,直到积分器输出为零,记录这个反向积分的时间T2。通过比较T1和T2的关系,就可以得到输入模拟信号的数字表示。 - 以 3 位二进制计数器为例说明双积分过程
在初始状态下,计数器清零,积分器输出为零。当开始转换时,对输入模拟信号进行积分,计数器开始计数。在T1时间结束时,计数器达到值(对于 3 位二进制计数器为 7),此时积分器的输出电压与输入模拟信号的平均值成正比。然后,切换到参考电压进行反向积分,计数器重新开始计数。当积分器输出为零时,计数器停止计数,此时计数器的值就代表了输入模拟信号的数字值。 - 定量分析
通过对双积分过程的数学推导,可以得到输入模拟信号Vin与计数器计数值N之间的关系。假设参考电压为Vref,时钟周期为Tc,则有Vin=2nNVref,其中n为计数器的位数。
转换精度是指 ADC 输出的数字信号与实际输入模拟信号之间的接近程度,通常用分辨率和量化误差来衡量。分辨率表示 ADC 能够分辨的模拟信号变化量,与 ADC 的位数有关,位数越多,分辨率越高。转换速度则是指 ADC 完成转换所需的时间,不同类型的 ADC 转换速度差异较大。例如,逐次渐近型 A/D 转换器的转换速度相对较快,而双积分型 A/D 转换器的转换速度较慢,但它具有较高的抗干扰能力。
综上所述,不同类型的 ADC 在转换过程、精度和速度等方面各有特点。在实际应用中,需要根据具体的需求来选择合适的 ADC,以满足系统的性能要求。


