非零上升时间造成的损耗
图 1 显示了 E 类功率放大器的典型开关波形。
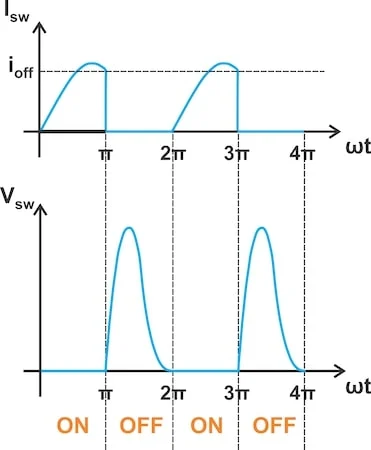
在 E 类放大器中切换电流和电压波形。
图 1.E 类放大器中的典型开关电流 (顶部) 和电压 (底部) 波形。
就在
晶体管导通之前(例如,在 ?t = 2π 时),开关两端的电压 (V西 南部) 返回 0 V。电压波形的斜率也为零 (电压西 南部/dt = 0) 的 ID 值。在满足零电压开关和零导数开关条件的情况下,开关电流在导通时间从零平稳上升。因此,在 OFF 到 ON 转换期间,开关两端的电压和通过它的电流都非常小,因此功率损耗可以忽略不计。
非零下降时间造成的损失
接下来,我们来看看 ON-to-OFF 转换期间的功率损耗。在图 1 中,开关在 ?t = π 左右关闭。电流波形显示开关电流瞬时变化我关闭设置为零。对于理想的 E 类放大器,我关闭是电源提供的直流电流 (I0).我们可以使用 “Unraveling the Design Equations of the E Class Amplifier” 中的分析轻松验证这一点。

图 2 显示了晶体管关闭时的放大器。0标记为绿色。
当晶体管关闭时,通过它的电流等于电源提供的直流电流的两倍。
图 2.当晶体管关闭时,通过它的电流是 I 的两倍 I0,电源提供的直流电流。
回顾一下,该放大器的理想操作需要一个可以瞬间切断 2I 大电流的开关0.由于实际的开关需要一些时间来切断电流,因此我们无法实现理想的操作。我们得到的不是图 1 中的波形,而是图 3 中的波形。
考虑开关非零 off-OFF 转换的开关波形。

图 3.切换考虑非零 off-OFF 转换的波形。
在这里,开关的非零关断时间会导致电流和电压波形之间重叠。因此,在这些间隔期间,IV 产物大于零,导致在 ON-to-OFF 转换期间产生功率损失。
在下一节中,我们将使用图 3 中的近似波形来计算关断开关损耗。在我们继续之前,请注意上图假设电流从我关闭在 t = π 到 0 在 t = π + θf.尽管学术著作中存在更、更复杂的模型,但线性模型足以让我们对电路的行为有一个基本的理解。
计算 Turn-OFF 功率损耗
图 4 显示了用于我们分析的开关波形的一个周期。为了简化我们的方程式,时间原点已更改为触发开关关闭的时刻。

切换用于功率损耗分析的波形
图 4.切换波形以用于功率损耗分析。
为了计算关断开关损耗,我们首先确定流过开关的电流和其两端的电压。然后,我们计算开关电压 (V西 南部) 和当前 (我西 南部) 在 OFF 过渡期间。
基于电流变化的线性模型,开关电流方程为:
$$i_{sw} ~=~ i_{off}(1~-~ \frac{\omega t}{\theta_f})$$
方程 1.
为了进一步简化,我们假设与 RF 周期相比,关断持续时间相对较短。因此,可以合理地假设谐振电路中的正弦电流在整个 Turn-OFF 间隔期间保持相当恒定。回到图 2,这意味着通过负载的瞬时电流 (我R) 和 I0在 OFF 间隔期间几乎保持不变。由于开关电流从我关闭为零,则通过
并联电容器的电流 (Csh因此,从 0 到我关闭.
我们通过对
电容器电流进行积分来获得电容器两端的电压(与开关电压相同):
$$V_{sw} ~=~ \frac{1}{\omega C_{sh}} \int_{0}^{\omega t} i_{c} \ d(\omega t)$$
方程 3.
请注意,电流的积分除以 ?Csh而不是按Csh独自。之所以进行此调整,是因为积分过程是针对 ?t 而不是仅 t 执行的。
代入我c从公式 2 中,我们得到:
$$V_{sw} ~=~ \frac{1}{\omega C_{sh}} ~\times~ \frac{i_{off}}{\theta_f} \int_{0}^{\omega t} \omega t \ d(\omega t) ~~\rightarrow~~ V_{sw} ~=~ \frac{i_{off}}{2 \omega C_{sh}\theta_f } (\omega t)^2$$
方程 4.
现在我们有了开关电压和电流,我们可以计算开关在关断转换期间的平均功耗:
$$P_{off} ~=~ \frac{1}{2 \pi} \int_{0}^{\theta_f} V_{sw} I_{sw} d(\omega t) ~=~ \frac{i_{off}^2}{4 \pi \omega C_{sh}\theta_f } \int_{0}^{\theta_f} (1~-~ \frac{\omega t}{\theta_f}) ~\times~ (\omega t)^2 \ d(\omega t)$$
方程 5.
上述方程式很容易简化为:
$$P_{off} ~=~ \frac{( i_{off} \theta_f)^2}{48 \pi \omega C_{sh} }$$
方程 6.
坠落时间如何影响效率?
我们暂时假设影响 E 类放大器的损耗机制是关断开关损耗。放大器的效率与理想的 100% 相比将如何变化?
为了估计效率,我们需要表示P关闭就分配给负载的功率 (PL).我们知道我关闭= 2I0、通过 RF 扼流圈的直流电流;从我们之前对设计方程的分析中,我们还知道 I0与正弦负载电流的幅度 (我R) 按以下方式分配:我0 = 0.537 × 我右
方程 7.
并且分流电容 (Csh) 是:
Cs小时 = 0.1836ω右L
方程 8.
将公式 7 和 8 与公式 6 相结合,我们得到:
$$P_{off} ~=~ \frac{( i_{off} \theta_f)^2}{48 \pi \omega C_{sh} }~=~ \frac{( 2I_0 ~\times~ \theta_f)^2 ~\times~ R_{L}}{48 \pi ~\times~ 0.1836}~=~\frac{( I_R ~\times~ \theta_f)^2 ~\times~ R_{L}}{24}$$
方程 9.
接下来,输送到负载的功率为:
磷L = 12右L我2右
方程 10.
,我们将方程 9 和 10 组合起来,得到:
磷哦ff = θ2f12×磷L
方程 11.
在我们继续之前,值得注意的是PL(公式 10)是由 E 类放大器传送到负载的射频功率。虽然我们不再处理完全理想的放大器,但我们正在考虑的特定非理想性不会改变输出功率。非零转换只会增加从电源汲取的功率 (P抄送).因此P抄送等于PL和交换机中耗散的功率 (P关闭):
磷cc = 磷L + 磷哦ff
方程 12.
放大器的效率为:η = 磷L磷cc = 磷L磷L + 磷哦ff = 11 + 磷哦ff磷L
方程 13.
使用泰勒级数展开式,当 x 远小于 1 时,我们可以用 1 – expansion 的 近似 \(\frac{1}{1~+~x}\)。注意到P关闭比PL,效率可以近似为:
η ≈ 1 - 磷哦ff磷L = 1 - θ2f12
方程 14.
让我们通过几个例子来巩固这些概念。
求给定下降时间的效率:两个示例
假设 E 类放大器中电流的关断间隔持续时间相当于整个工作周期的 30 度。放大器的效率是多少?
在我们使用方程 14 回答这个问题之前,我们需要用弧度表示下降时间。代入 θf= π/6 放入效率方程中,可生成:
$$\eta ~\approx~ 1~-~ \frac{\theta_f^2}{12} ~=~ 1 ~-~ \frac{(\pi/6)^2}{12} ~=~97.7 \ \%$$
方程 15.
接下来,让我们考虑一个情况,其中下降时间以纳秒为单位,而不是以百分比为单位。
工作频率为 1.2 MHz 的 E 类放大器使用下降时间tf= 20 纳秒。如果放大器的理想输出功率为 80 W,则计算放大器的效率以及关断转换期间晶体管中的功耗。
同样,我们首先以弧度为单位计算下降时间:
θf = cω × tf = 2π × 1.2 × 106 × 20 × 10?9 = 0.151 rad 拉德
方程 16.
然后,我们通过应用公式 14 来获得效率:
$$\eta ~\approx~ 1~-~ \frac{\theta_f^2}{12} ~=~ 1 ~-~ \frac{(0.151)^2}{12} ~=~99.8 \ \%$$
方程 17.
由于理想的输出功率为PL= 80 W,则在关断间隔期间耗散的功率为:
$$\eta ~\约~ 1~-~ \frac{\theta_f^2}{12} ~=~ 1 ~-~ \frac{(0.151)^2}{12} ~=~99.8 \ \%$ $ 方程 18.



