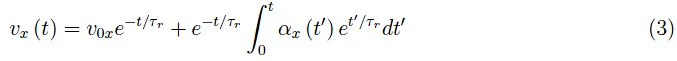由阿尔伯特·爱因斯坦 (Albert Einstein) 1,2以及随后的保罗·朗之万 (Paul Langevin, 1908) 通过随机微分方程进行研究。与在粘性流体中移动、与构成流体的分子随机碰撞的粒子不同,在我们的模型中,单个
电子在二维晶格中移动,与分配在晶格节点中的原子核随机碰撞。
由于德鲁德-洛伦兹模型是基于经典力学,我们必须应用牛顿第二定律 F=m e * a,其中 F 是作用在有效质量 m e *的电子上的力的合力,而 a=dv/dt是加速度,v 是速度。所得结果为 F = Fu (t) + R(v),其中 Fu (t) 是单次碰撞中交换的力,而 R(v) 确定碰撞导致的速度阻尼(动能损失)。然而,在布朗模型中,R(v) 考虑了介质的粘度。
我们顺便注意到一些作者将 R 等同于摩擦力。实际上,该力是动态阻力,与摩擦力不同,如果粒子静止,则该力为零。 R(v) 的方向与速度相反:R(v) = ?bv,其中 b > 0(阻尼系数 )。将这些项代入表达
牛顿第二定律的方程中,我们得到的朗之万方程:

电力电子科学笔记:用 Mathematica 模拟
石墨烯中电子的运动
这里τ r = m e * e/b 是弛豫时间,即碰撞与下碰撞之间的平均时间(我们在上一期中临时引入了这个量);α (t) 是每单位有效质量的碰撞中交换的力。由于碰撞的随机性,一个量是一个随机变量。由此可见,朗之万方程是一个随机微分方程。
统计分析
将方程(1)投影到我们研究电子运动的参考系的坐标轴上,我们得到以下解耦随机微分方程组:

电力电子科学笔记:用 Mathematica 模拟石墨烯中电子的运动
从形式的角度来看,我们可以讨论系统(2),就好像已知项是实变量 t 的通常实函数一样。因此,这是两个(解耦)一阶线性微分方程。应用寻找解决方案的标准程序并考虑明显的初始条件 v (0) = v0,我们得到:
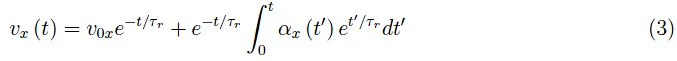
电力电子科学笔记:用 Mathematica 模拟石墨烯中电子的运动
对于v y ( t ) 也是如此。在我们的模型中,电子之间的碰撞是弹性的,因此我们不考虑它们,这使我们能够将过程的分析集中在单个电子上。
对类型 (3) 的解决方案应用统计分析。如上所述,α x 和α y 是随机变量。我们回想一下,对于确定性变量,在给定时刻t假定的值地确定在任何时刻 t′ > t 假定的值;对于随机变量,预测值确定变量在 t' > t 时呈现给定值的概率。在物理兴趣的情况下,该概率不依赖于时间(平稳过程)。更有趣的是遍历过程:这些是特殊的平稳过程,其中随机变量的时间平均值与统计平均值一致。
在这种情况下,实验/计算优势是巨大的,因为时间平均值的计算理论上需要无限的观察时间。从物理上讲,这意味着在很长的时间间隔内(在无限的极限内),所检查的数量呈现相应统计集中的所有可能值。由此可见,统计平均值返回时间平均值。然而,应该指出的是,这是一个启发式结论,目前正在研究给定过程遍历的必要和充分条件。
在我们的例子中,我们得到 (2) 的解,它仅具有形式或更好的象征意义,因为我们无法明确α x ( t ) 、 α y ( t ) 。对于上述情况,根据所获得的解的解析表达式,我们尝试表达统计平均值v x ( t ),众所周知,它是v x ( t )的方差,假设 v x ( t ) = 0 ,类似地我们确定分量v y ( t )的方差。在信号理论的术语中,这些量表示平均功率,并且该名称也用于所讨论的情况。为了确定速度矢量的笛卡尔分量的方差,需要知道分量α x、α y的方差。为此,我们介绍一些关于随机变量的一般概念。
如果z ( t ) 是相对于遍历过程的随机变量,则其统计平均值 ? z ( t )? 与时间平均值一致;通过重新定义z值的范围,我们仍然可以假设 z ( t )= 0;由此可见,方差 z ( t ) 2告诉我们z ( t ) 距离平均值有多远。同样重要的是方差的平方根,定义为我们已知z ( t ) 的不确定性,并用 Δ z表示。这些量可以从功率谱w ( f )中获得,功率谱对从 0 到 +∞ 的所有频率f 的积分返回平均功率z ( t ) 2。另一个统计上有趣的量是 z ( t ) z ( t ′ ) 当且仅当z在时间t ′ > t时采用给定值的概率不依赖于z在时间t时采用的值时,它才为零。反之亦然。
在种情况下,我们会说随机变量z假设的值是 100% 不相关的。因此,我们将 z ( t ) z ( t ′ )称为z的自相关函数;更具体地说,设置τ = t ′ t,自相关函数可写为:

请注意,自相关函数具有幂(即 z2)的维数,并且是一个偶函数:通过 t 与t ′交换的不变性,可以得到 phi (?τ ) = phi (τ ) ;此外,它在无穷大时消失,因为有限值与在无穷大找到指定值的概率之间不存在相关性。自相关函数和功率谱之间有什么联系?的维纳辛钦定理提供了答案:功率谱是自相关函数的傅里叶变换。由此可见,平坦功率谱返回一个自相关函数,该函数是一个以τ = 0 为中心的狄拉克
delta。因此,我们有一个 100% 不相关的随机变量,称为白噪声。这个名字来源于功率谱的平坦度,就像颜??色一样,如果它们在统计上对叠加有相同的权重,就会产生白色。
也就是说,我们证明在合理的假设下,随机变量α x ( t )和 α y ( t ) 由白噪
声表示。为此,我们用τ u 表示碰撞的平均持续时间。显然τ u τ r 因为碰撞在所考虑的过程的时间尺度上是瞬时的。
由此可见, α x ( t ) α x ( t ) 仅当t t + τ时才非零,即t实际上与t重合。反之亦然,如果t ′ ? t + τ则 α ( t ) α ( t ′ )? = 0。换句话说,α ( t ) 具有白噪声的所有特征。从物理上讲,这意味着电子失去了对单独碰撞的记忆。同样的结论也适用于α y ( t )。因此,这些量的特征是平坦的功率谱。
这些结果使我们能够从给定初始条件下方程 (2) 的解开始确定 vx(t) 2、vy(t) 2 。随后的积分(即传递到二阶方程)使我们能够确定 x(t) 2、 y(t) 2 ,从而确定电子始终位置的不确定性 Δ x 、 Δ y 。
时域分析
上一期提出的框架计算量很大。继续分析,我们已经消耗了二十二页的笔记。主要困难在于积分的计算,因为它是计算平方函数的问题,因此成为二重积分。对于基于某些软件的程序,我们想到了Mathematica环境。准确地说,我们生成一个具有特定平均值(可以任意设置为 0)并具有指定方差的随机实数列表。
通过 ListLinePlot 指令,Mathematica绘制出完全具有白噪声外观的图形。然而,生成的列表无法用于微分方程组 (2) 的积分;想法是通过插值指令来处理它;通过这种方式,我们迫使Mathematica内核生成一个成熟的函数;显然,内核不会提供这个函数的解析表达式,但它仍然会输出一个名为InterpolatingFunction的对象。
这不应该让我们担心,因为现在我们在Mathematica笔记本中拥有了一个成熟的函数,因此通过使用 NDSolve 指令求解方程 (2),我们再次获得一个可以绘制的 interpolatingFunction 类型的对象。然而,我们对电子的轨迹感兴趣,因此我们必须用x ( t ) 、 y ( t ) 重写方程 (2) 以获得二阶方程。使用Mathematica重复该过程,我们得到如图 1 所示的行为。电子的不规则路径反映了与晶格碰撞的随机性。
为了模拟第二个电子的运动,我们关闭内核,然后运行例程。结果是一个与图 1 中的图形不同的图形,虽然它保留了不规则趋势,但它将探索晶格的不同区域。原则上,如果N 1 是电子总数,则通过运行例程N次,我们期望轨迹随机分布。从物理上讲,这意味着没有净电荷流动,这是预期的。
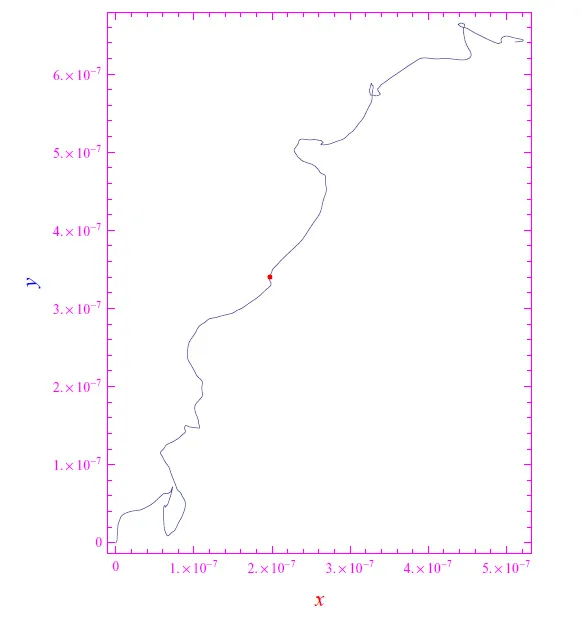
图 1:电子轨迹(红点)。数量 x 和 y 以无量纲单位表示。
现在让我们想象一下在x轴负方向上施加均匀静电场。由此可见,除了碰撞之外,单个电子还受到沿x轴正方向定向的恒定力。通过将此常数项添加到我们的方程中并执行相应的例程,我们获得了图 2 的轨迹,从中我们看到了更规则的趋势。此外,与之前的情况不同,通过执行例程N次,我们发现输出保留了轨迹的趋势。从物理上讲,这意味着所施加的电场决定了速度漂移项,从而在晶格中建立了净电荷流。
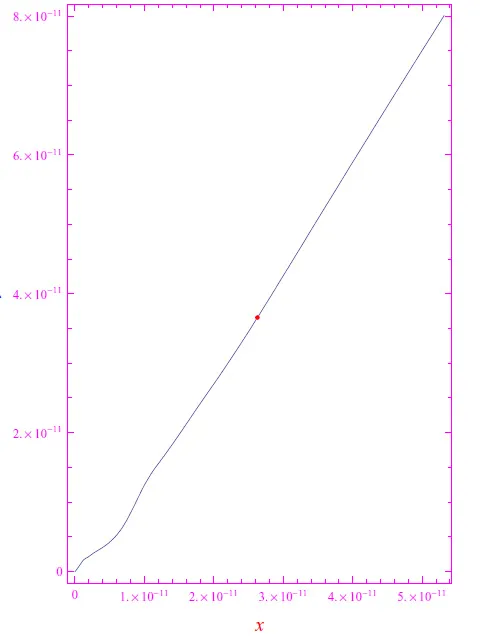
图 2:存在均匀静电场时电子(红点)的轨迹。
结论
在这个简单的二维模型中,我们将分析过程与计算过程进行了比较。个基于统计分析,而第二个基于时域分析。这是两个程序,不是对立的,而是互补的。计算方法是分析方法的结果,因为它提供了所研究过程进展的实时想法。