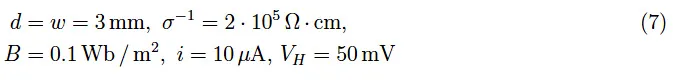在本教程中,我们将使用前几期研究的 Drude-Lorentz 框架。我们记得这个模型完全基于经典力学。的“外来”成分是
电子的有效质量m * ;这是一种数学技巧,使我们能够将电子视为不受力的经典粒子。通过这种方式,避免了量子复杂性,因为我们必须考虑晶格离子施加的周期性势能。在极端合成中,我们有以下情况:电子与离子非弹性碰撞,失去所有动能。
施加均匀静电场 E 使电子加速;加速度矢量的大小为a = eE/m *,其中e是电子电荷的。如果τ r 是碰撞与下碰撞之间的时间(弛豫时间)的平均值,则电子在经历新的碰撞的瞬间的速度矢量的大小为v d = aτ r,其中我们认识上一期我们在软件中重建的漂移速度。继续讨论相应的向量(请记住,在我们的符号中,电子电荷为 - e < 0),我们得到:

其中n是电子数密度。电流密度矢量 j 的方向与电场类似,而漂移速度的方向相反。从方程(1)欧姆定律可知:

电力电子科学笔记:
半导体中电子和空穴迁移率的测量
其中σ是电导率。
在室温下,刚才描述的场景再现了金属的电气行为。这些结果很容易扩展到半导体,只要空穴的贡献包含在 σ 的表达式中,该表达式的有效质量m * h通常不同于电子质量。假设两个电荷载流子具有相同的时间τ r 值是一个很好的近似(更复杂的模型1假设τ r 不仅取决于电荷载流子的符号,还取决于单个电子/空穴)。
通过定义电子和空穴的迁移率,电导率的解析表达式呈现出更易于管理的形式:

方程(3)从微观角度定义了迁移率。考虑到上面写的公式,我们得出一个宏观定义,根据该定义,电荷载流子的迁移率是其每单位电场的漂移速度。从实验的角度来看,数量(3)可以通过霍尔效应来确定。在深入研究十九世纪发现的这一过程之前,我们必须澄清电磁学的一些概念。
磁场:B 还是 H?
在有关电磁学的旧出版物中,假设 H(磁场强度)为基本矢量,B(磁感应强度)为导出矢量。然而,为了保持电学量和磁学量之间的对称性,有必要假设B为基本矢量。令人误解的是,在静电学中,电场强度 E 被假定为基本矢量,而
电感应 D 是导出矢量。但是,当查看麦克斯韦方程组以建立电荷和电流之间以及微分算子Div和Curl之间的对称性时,我们必须假设 B 为基本向量。在许多有关固态物理学的文献中1,H 出现在方程中,指定该量用 B 表示,因为没有考虑铁磁材料。为了避免误解,在我们的方程中,B 将显示为磁场。
另一个问题:“SI 单位制还是高斯单位制?”答案取决于读者。如果他是物理学家,他会回答:“高斯”。如果他是一名工程师,他会回答:“SI”。高斯系统更适合亚原子过程,而 SI(或有理化 MKS)则适合宏观系统。我们将使用 SI,其中 B 以 Wb / m 2为单位进行测量。
在霍尔效应中,洛伦兹力F发挥着关键作用,即作用在磁场 B 中以速度 v 移动的电荷q上的力。在 SI 单位制中:

霍尔效应
让我们考虑图1所示的实验配置,其中我们将恒定电势差V 0施加到具有边缘L、d、w的平行六面体形状的金属导体的端部。在均匀性和各向同性的条件下,将建立沿y轴定向的均匀静电场:E = (0 , E, 0)。这导致电流密度 j 与电场矢量 E 平行且一致,而速度矢量则定向为相反方向(图 1 中的虚线)。构成导体的材料的均匀性和各向同性与热平衡相结合,保证了如上所述排列的直线轨迹。
均匀静磁场 B = (0 , 0 , B ) 的激活决定了如图 1 所示方向的洛伦兹力 F,该力使单个电子的轨迹偏转。由于导体的任何横截面都是开路,因此电子将无法无限期地流动。终结果是其中一个边缘带有过量的负电荷(图 1);然后将建立称为霍尔场的电场 E H 。更准确地说,当霍尔场施加的力与洛伦兹力 F 大小相等且方向相反时,就会达到平衡,如图 1 中的力图所示。很容易得出表示洛伦兹力的矢量积因为速度矢量与磁场正交。
应用动态平衡条件,我们很容易得到E H = v d B。现在,如果我们任意取导体的横截面 Σ,则在点 1 和点 2(图 1)之间建立电势差V H = E H d(霍尔电压)。考虑到E H 的表达式并用电流密度j表示v d ,因此电流强度i = jS ,其中S = wd是 Σ 的面积,我们得到:

电力电子科学笔记:半导体中电子和空穴迁移率的测量
其中R H = 1 /ne是霍尔系数,它是电荷密度的倒数。考虑到(3)中的个,我们终得到:

电力电子科学笔记:半导体中电子和空穴迁移率的测量
在等式(5)中,指定了B和w 。 V H、 i量是可以测量的,因此我们计算R H;假设电导率 σ 已知,(6)允许我们确定 e。不幸的是,对于金属,由于电子数密度值较高,VH 太低;事实上,霍尔电压与R H 成正比,即与电荷密度的倒数成正比。对于半导体来说,这种情况不会发生(这里电荷密度降低了 10 5数量级),注意到通过引入空穴迁移率可以轻松扩展所获得的结果。我们邀请读者确定p型硅棒的空穴迁移率,其中:
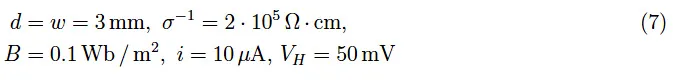
电力电子科学笔记:半导体中电子和空穴迁移率的测量
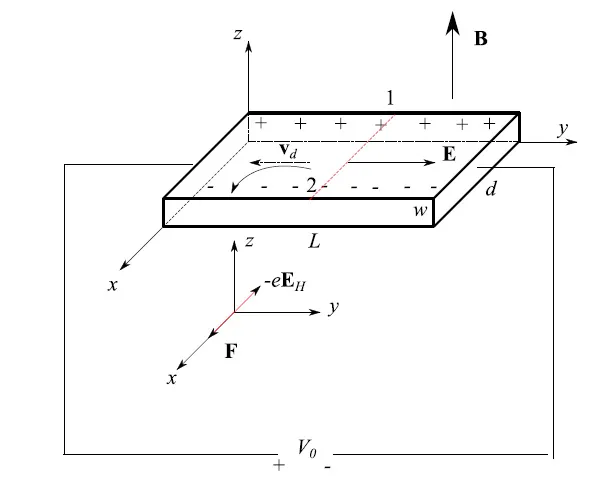
图 1:研究霍尔效应的实验装置。虚线矢量是没有磁场时的漂移速度。通过激活磁场,电子受到洛伦兹力的作用,从而弯曲各个轨迹。
结论
所提出的实验使我们能够确定室温下的迁移率。更复杂的是一个模型,该模型考虑了极端温度,例如板空间
探针上的半导体器件中出现的温度。相反的限制(高温)也是电力电子的典型问题。