如今,我们经常可以找到典型失调电压相对于系统要求非常低的运算放大器。如果这些运算放大器中的一个符合项目预算,那么在设计过程中我们几乎不需要考虑失调电压。
但有时,运算放大器操作的这种非理想方面会以明显的方式影响电路的性能。我在本文中的目的是提出一种通过 SPICE 仿真分析失调电压影响的方法。
我将用作示例的电路是我在前三篇文章中探索过的精密电流泵。下图提供了该电路的原理图和理论上的输入输出关系。
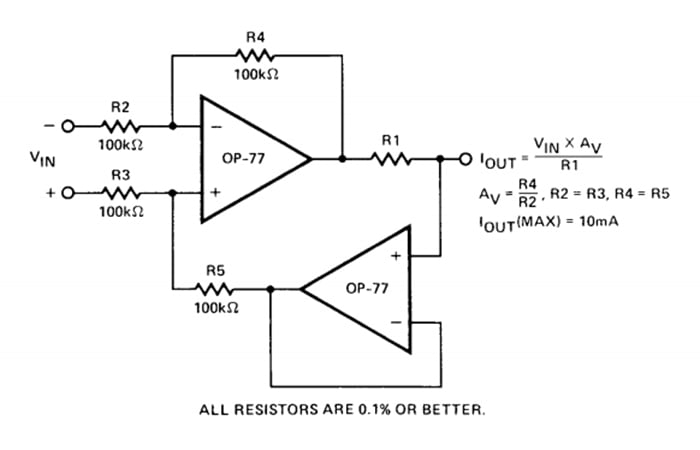
运算放大器内部不可避免的组件不匹配会导致 0 V 差分输入产生非零正或负输出电压。输入失调电压是必须施加到输入端子之一的电压,以补偿不匹配,从而实现 0 V 输入的 0 V 输出。
偏移电压是有问题的,因为它会导致运算放大器偏离产生更好结果和更用户友好的理想模型。此外,无法高精度预测这种偏差的严重程度:数据表只能使用单个数字来描述失调电压,前提是它指的是典型或失调电压。
要更全面地了解失调电压行为,您需要查看表征大量器件(具有相同部件号)时获得的分布。
在上一篇关于使用容差和温度模拟电流泵性能的文章中,我使用 AD8606 运算放大器进行电流泵模拟。AD8606 数据表提供了下图,以帮助我们了解该部件编号的失调电压值分布:
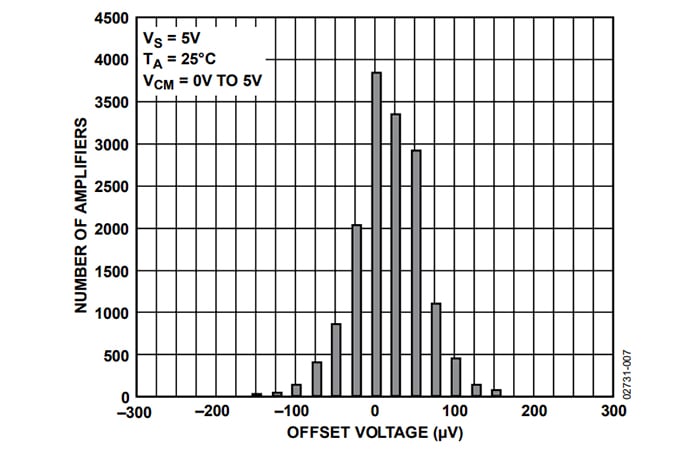
分布的形状类似于正态(又名高斯)分布的形状,这并不奇怪,因为当测量值受多个随机变化的参数影响时,我们期望正态分布。
如果我们想将偏移电压纳入我们的电路分析,我们添加一个与运算放大器的正输入端或负输入端串联的直流电压源。结果是一个看起来像这样的电路模型:
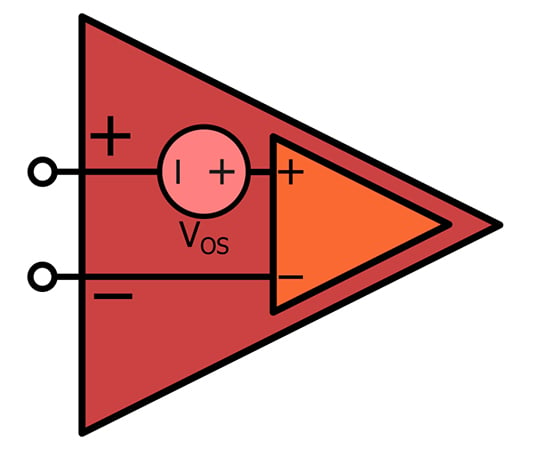
橙色运算放大器是一个理想的运算放大器,或者至少是一个没有偏移电压的运算放大器。红色运算放大器代表我们通过将理想运算放大器与直流电压源相结合而创建的“更真实”的运算放大器。
电压源的值通常是典型失调电压或失调电压——如果您必须选择一个值的话。在 SPICE 仿真中,我们可以选择许多不同的值。
在之前的文章中,我们使用 LTspice 的蒙特卡罗(缩写为mc)函数来产生与电阻器容差相对应的电阻值变化。然而, mc函数根据均匀分布生成随机数。我们想要具有正态分布的随机数,因此我们将改用高斯函数。这是电路:
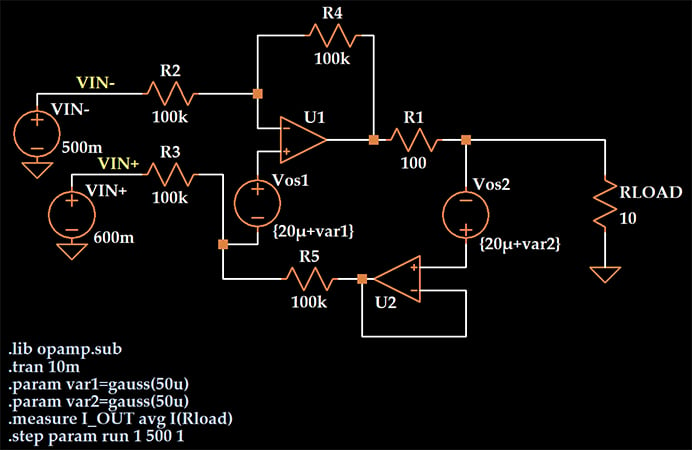
我在这里的目的是仅分析偏移电压的影响。所有电阻都设置为无公差的标称值,运算放大器是 LTspice 的理想单极运算放大器,而不是对应于实际组件的宏模型。
我希望失调电压反映我们在真实运算放大器中可能看到的变化,并且由于我在之前的仿真中使用了 AD8606,所以我决定根据 AD8606 的失调电压特性来设计此仿真。换句话说,我试图近似我们在本文前面看到的直方图所传达的失调电压分布。
AD8606 数据表给出了 20 μV 作为典型的失调电压值,因此我将其用作表示失调电压的电源的标称值。传递给高斯函数的参数是随机生成的数字的标准差。因此,我的失调电压值定义为 {20μ + gauss(50μ)},表示均值为 20 μV、标准差为 50 μV 的高斯分布。
正如我们将在下一篇文章中看到的那样,这种均值和标准差的组合产生的分布与 AD8606 的直方图相当一致。这种相同的技术可用于近似具有近似正态分布的失调电压值的任何运算放大器部件号的失调电压规格——您只需根据需要更改平均值和/或标准偏差。
免责声明: 凡注明来源本网的所有作品,均为本网合法拥有版权或有权使用的作品,欢迎转载,注明出处。非本网作品均来自互联网,转载目的在于传递更多信息,并不代表本网赞同其观点和对其真实性负责。