传统的 AM 和 DSB-SC 技术
首先,让我们简要回顾一下双边带抑制载波 (DSB-SC)和传统 AM调制的方程。在 DSB-SC 调制中,调制信号是通过将消息信号 ( m ( t )) 乘以载波 ( c ( t ) = A c cos(ω c t )) 生成的:
sout(t) = m(t) × Accos(ωct)
等式 1。
为了确保载波保留在传输频谱中,传统 AM 采用以下公式来产生调制信号:
sout(t) = Ac(1 + μm(t))cos(ωct)
等式2。
在这两种情况下,我们都可以使用模拟乘法器来直接计算输出信号。平方律调制器是实现这种乘法的另一种常见方法。
平方律调制器如何生成 AM 信号
平方律调制器的思想是两个函数之和的平方生成与两个函数的乘积成比例的叉积项。假设非线性器件的输入输出特性可以表示为:
y(t) \大约 α1x(t) + α2x2(t)
等式 3。
等式 3。
如果我们将消息 ( m ( t )) 和载波 ( c ( t ) = cos( c t )) 波相加,并将组合信号传递给上述平方律特性,我们得到: y(t) ≈ α1m(t) + α2m2(t) + α2cos2(ωct) + (α1 + 2α2m(t))cos(ωct) 等式 4。
上式中的一项是所需的 AM 波。公式 5 重写了该术语,以便于与公式 2 中的传统 AM 信号进行比较:
y(t) ≈ α1m(t) + α2m2(t) + α2cos2(ωct) + (α1 + 2α2m(t))cos(ωct) 等式 5。
该信号使用的调制指数为: μ = 2α2α1
等式 6。 但我们如何将所需的 AM 波与其他光谱分量分开呢?让我们在下一节中探讨这个问题。
提取 AM 信号

假设m ( t ) 是带宽B的低通信号,如图 1 所示。
如果频率的超过带宽,则消息信号的频谱具有零功率。
图 1.消息信号的频谱|f| 的功率为零> B .
让我们确定公式 4 中其他组件的频率范围。
首先,我们检查m 2 ( t )的带宽,即消息信号的平方。当我们对m ( t ) 进行平方时,我们实质上是在时域中将信号与其自身相乘。
根据卷积定理,时域中的乘法对应于频域中的卷积。如果M ( f ) 是m ( t )的傅里叶变换,则m 2 ( t )的傅里叶变换就是M ( f ) 与其自身( M ( f )* M ( f ) )的卷积。由于卷积的基本性质,我们还知道M ( f )* M ( f )的带宽是M ( f )带宽的两倍。图 2 对此进行了说明。

非线性平方律装置的输出频谱。
图 2.具有平方律特性的非线性器件的输出频谱。
我们可以这样解读这个图:
消息信号 ( m ( t ))的频谱以蓝色显示。
绿色频谱显示m 2 ( t )占据的频率范围。
所需信号 ( s out )的频谱以橙色显示。
紫色脉冲函数由载波的平方 (cos 2 ( c t )) 创建。
m 2 ( t )频谱的确切形状不是我们在这里关心的。重要的是它的傅立叶变换仅限于 2 B Hz 以下的频率。
假设其频谱不与m ( t ) 和m 2 ( t ) 的频谱重叠,则可以使用带通滤波器将所需信号与其他项分离。由图2可知,避免光谱重叠的条件是: fc ? B ≥ 2B → fc ≥ 3B 等式 7。
在现实世界中,载波频率与基带信号带宽的比率(f c / B)通常为100到300,因此很容易满足这个条件。因此,我们可以使用平方律装置和带通滤波器(图 3)来生成 AM 波。
平方律调制器的框图
带通滤波器调谐到载波频率 ( f c ),理想情况下带宽为 2B。图 2 显示滤波器应具有 ( f c – B ) – 2 B ≈ f c的过渡带,以抑制零频率附近的频谱分量。
一些 AM 调制器要求不太严格的约 2 f c的过渡带,因为它们的结构消除了以f = 0为中心的频谱分量。对于这些调制器,接近的不需要的频谱以 3 f c为中心。不过,这是改天再讨论的事。现在,让我们看一些平方律调制器的实际示例。
实际电路实现
平方律调制器中的非线性器件可以是半导体
二极管、BJT 或 FET 器件。然而,由于其噪声性能较差,二极管并不常见。双极
晶体管也有缺点,因为它们会产生需要过滤的高水平杂散频率。图 4 显示了围绕 BJT 器件构建的平方律调制器的基本原理图。
基于 BJT 的平方律调制器的电路图。
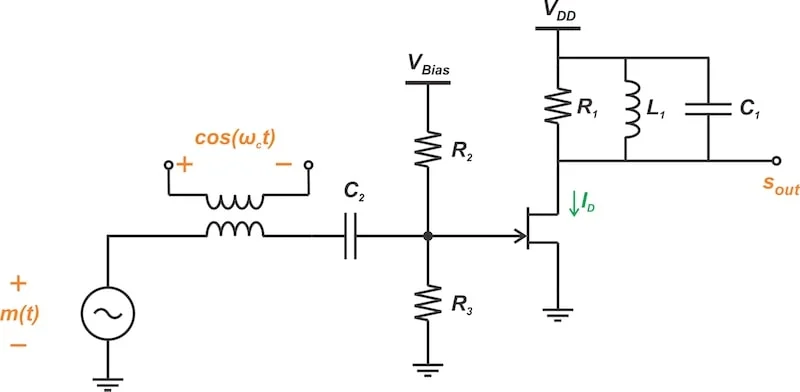
图 4.使用 BJT 作为非线性器件的平方律调制器。
在此实现中,晶体管提供非线性,LC 电路滤除高次谐波分量。
场效应管的实现
由于 FET 具有接近平方律的输入输出特性,因此成为平方律调制的。图 5 说明了 FET 实现,它使用
变压器将载波与消息信号组合起来。
基于 FET 的平方律调制器的电路图。
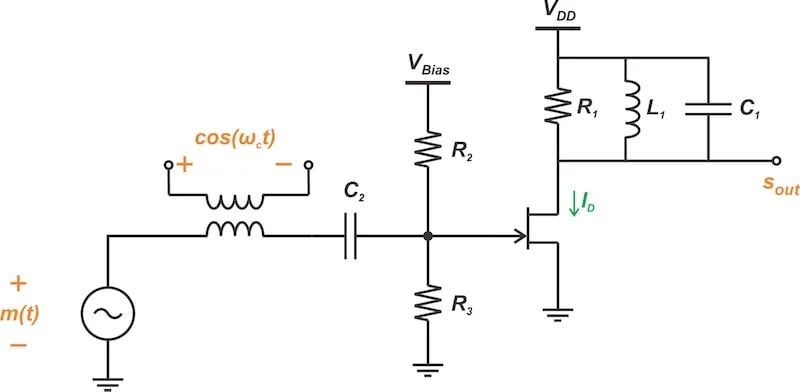
图 5.基于 FET 的平方律调制器。
基于叠加原理,我们还可以使用两个电阻来生成m ( t )与载波之和。图 6 显示了使用此方法的 FET 平方律调制器。未示出偏置电路。
基于 FET 的平方律调制器,使用两个电阻器来组合消息和载波。
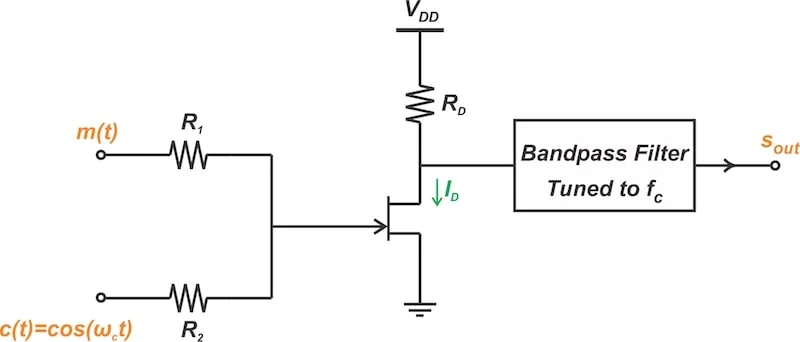
图 6.电阻网络可用于生成消息和载波的总和。
使用平方律调制器生成 DSB-SC 信号
我们已经看到平方律调制器可以生成传统的 AM 信号,但是 DSB-SC 信号呢?事实证明,如果器件的输入输出特性没有线性项(换句话说,如果等式 3 中? 1 = 0),平方律调制器可以生成 DSB-SC 信号。在这种情况下,带通滤波器输出端的信号为:
sout = 2α2m(t)cos(ωct) 等式 7。




