许多
电子系统需要计时机制。这通常是通过时钟信号来完成的,时钟信号是特定频率的方波。对于许多应用,时钟信号是通过方波振荡器在系统内生成的。然而,该方波信号也可以作为系统的输入。
由于许多模拟和数字电路都可以用作方波振荡器,因此我们的目标是涵盖这两种类型;然而,在本文中,我们将讨论模拟振荡器的设计,介绍其工作原理,并回顾其优点和缺点。
使用非稳态多谐振荡器的
运算放大器方波发生器
我们将研究的个电路是称为非稳态多谐振荡器的单运算放大器电路,如图 1 所示。
用于生成方波的单运算放大器非稳态多谐振荡器。

图 1.用于生成方波的单运算放大器非稳态多谐振荡器。
如果您暂时忽略从输出 V OUT到负输入 V c 的RC 反馈,您可能会将此电路的其余部分识别为具有迟滞的施密特触发器。施密特触发器具有正反馈,并且只有两个稳定工作点(V OUT = V DD或V OUT = V SS)。正如我们将解释的,非稳态多谐振荡器配置依赖于这种正反馈和迟滞。
电路启动后,电容器( C) 完全放电到地面。由于任何放大器的输入之间都存在内部偏移,因此正反馈将确保输出被驱动到两个稳定状态之一(取决于内部偏移是正还是负)。
现在,我们假设 V OUT在开始时被驱动至正电源轨 (V DD )。此时,V c将开始通过
电阻器R 3充电 ,并且 V p处的电压可以使用电阻分压器方程计算:
Vp1=VOUTR1R1+R2=VDDR1R1+R2
从这里开始,V c将继续充电,直到它变得略大于 V p处的阈值电压。此时,V OUT将下拉至负电源轨 (V SS ),并且 V c将开始放电。
当 V OUT的新值等于 V SS时,我们还有一个新的阈值电压:
Vp2=VOUTR1R1+R2=VSSR1R1+R2
接下来,V c将继续放电,直至低于 V p处的电压。然后,输出将被驱动回正电源轨 V DD。该过程将周期性地继续,从而在运算放大器的输出端产生方波。
运算放大器方波仿真:电压波形和频率
对于图 1 的电路,我们插入一些元件值和仿真性能:
R 1 = R 2 = 10 kΩ
R 3 = 1 kΩ
C = 1 微法
VDD = + 5V
VSS = -5V
在图 2 中,我们绘制了 V c、V OUT和 V p的电压波形。
运算放大器非稳态多谐振荡器方波振荡器仿真。顶部:VOUT(绿色)。底部:Vc(蓝色)和 Vp(红色)
图 2.运算放大器非稳态多谐振荡器方波振荡器仿真。 顶部:V OUT(绿色)。底部:V c(蓝色)和 V p(红色)
正如我们所看到的,V c充电和放电到先前由R 1和 R 2之间的电阻分压器以及电源电压定义的跳变点。跳变点 V high和 V low定义为:
V高=Vp1=5(10 k10 k+10 k)=2.5 V $$ V_{低} = V_{p2}= -5(\frac{10 \text{ k}}{10 \text{ k} + 10 \text{ k}}) = -2.5 \text{ V}$ $

图 2 中波形的频率为 451 Hz。它由图 1 中在 V high和 V low之间对电容器充电和放电所需的 R 3和 C RC 时间常数定义。
为了准确计算电路的元件频率,我们必须利用 RC 电路的充电/放电方程。充电方程的一般形式为:
V(t)=Vmax+(V初始?Vmax)e?tτ
求解该方程中的 t,我们得到: t=?τ?ln(Vmax?V(t)Vmax?V初始) 现在,如果我们假设从 V low充电到 V high 的时间,其中 V max = V DD,并且我们将充电和放电的时间加倍,我们就可以得到输出周期:
T=2t=?2τ?ln(VDD?VupVDD?Vlow)=?2RC?ln(VDD(1?R1R1+R2)VDD?VSSR1R1+R2) 该方程表明RC 时间常数占主导地位,而 R 1和 R 2的值与周期的关系较弱,因为它们会改变电容器必须充电和放电的跳变点。
如果我们代入 R 1、R 2、R 3和 C的值,我们会得到 455 Hz 的周期,这几乎与模拟中的 451 Hz 频率相匹配。
该电路简单、有效,并且支持低频和高频,但受到开关事件期间驱动输出的运算放大器压摆率的限制。缺点是输出摆幅无法变小,从而对频率设置硬性限制,因为输出必须在轨之间摆幅。
要使用从地 (0 V) 摆动到 V DD 的单电源运算放大器构建此电路,连接到电容器和电阻器 R 1 的接地节点必须更改为中等范围电压 - 通常为
使用 BJT 的基于
晶体管的方波振荡器
非稳态多谐振荡器也可以用分立晶体管代替运算放大器制成。图 3 显示了使用双极结型晶体管 (BJT) 的示例。
基于 BJT 的非稳态多谐振荡器,用于产生方波。
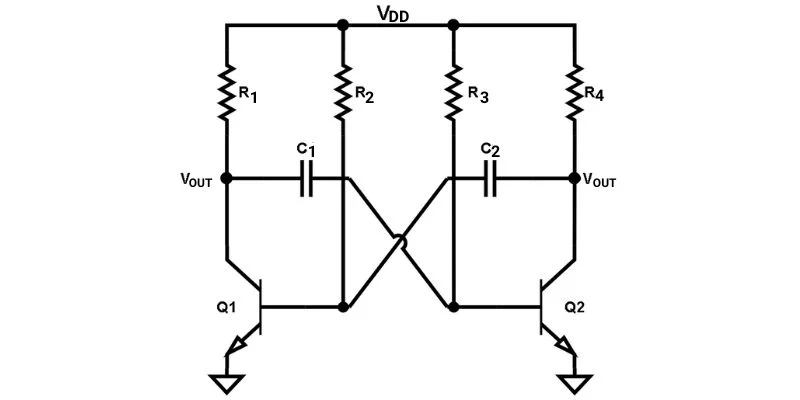
图 3.用于生成方波的基于 BJT 的非稳态多谐振荡器。
该电路启动后,一个晶体管(假设为 Q2)将进入“截止”区域,在此区域不传导电流。这将导致集电极节点(Q2 顶部)充电至VDD。
同时,Q1将饱和从而导通电流。这将导致连接到 Q2 基极的 C 1节点通过 R 3充电,直到 Q2 进入饱和状态。当被推至饱和时, C 2 右侧的急剧压降会在 Q1 基极引起严重的负响应,从而将其推至截止状态。
这种推挽行为持续发生,在 Q1 和 Q2 的集电极上产生输出电压波形。输出是频率相同但相位相反的方波。由于Q1和Q2的基极分别通过R 3与C 1和R 2与C 2的RC电路进行充电/放电,因此我们可以将发生器的输出周期定义为:
T=t1+t2
t1=0.69R3C1
t2=0.69R2C2
在瞬态波形中,t 1是Q1集电极输出的脉冲宽度,而t 2是Q2集电极输出的脉冲宽度。从等式中可以看出,t 1不必等于t 2,因此我们可以创建可变占空比的矩形波形。
图 4 的仿真结果演示了这种行为。对于此仿真,我们设计的电路具有 50% 占空比,且 t 1 = t 2。
双极晶体管非稳态多谐振荡器输出,具有对称输出。
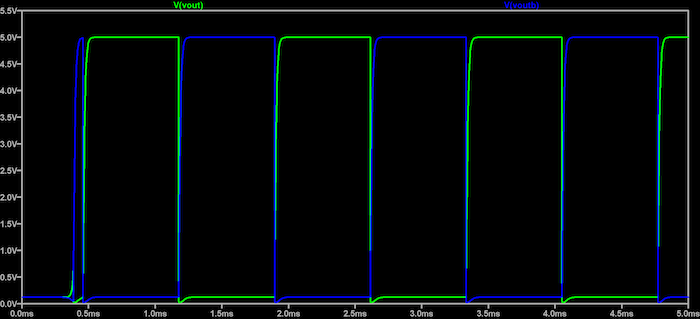
图 4.具有对称输出的双极晶体管非稳态多谐振荡器输出。
该模拟的组件值为:
R 1 = R 4 = 1 kΩ
R 2 = R 3 = 100 kΩ
C 1 = C 2 = 10 nF
BJT 是标准2N2222 NPN。因此,我们的基本方程的预期时间常数是: t1=t2=0.69RC=0.69(100 kΩ)(10 nF)=690 μs 我们的模拟测量结果为 681 μs,接近我们的设计值 690 μs。
我们还可以更改此设计以具有非对称性能。如果我们将 R 2的电阻减半为 50 kΩ,则可以将 t 2的周期更改为 345 us。更改后该电路的仿真结果如图 5 所示。
双极晶体管非稳态多谐振荡器输出,具有非对称输出。
图 5.具有非对称输出的双极晶体管非稳态多谐振荡器输出。

从图 5 中,我们看到能够创建具有易于调节占空比的非对称输出矩形波。仿真结果为 t 1 = 681 μs 和 t 2 = 335 μs,这再次接近我们的设计方程预测的结果。
总体而言,与运算放大器振荡器相比,基于 BJT 的非稳态多谐振荡器具有更大的灵活性。虽然结构稍微复杂一些,但它不需要负电源并产生输出及其补充。它还能够形成可
变频率和占空比的通用矩形波,而不是纯可变频率的方波。




