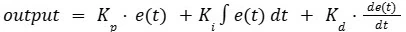控制
直流电机的速度需要电机的反馈和能够根据所需性能调整电机输入的控制算法。比例积分微分 (PID) 控制器是实现这一目标广泛使用的方法之一。
在本教程中,我们将在 Python 中模拟直流电机的简单 PID 控制器,而不使用类。控制器的目标是根据编码器的反馈来调整电机的速度,并由 PID 环路处理控制逻辑。
如何使用 Python 模拟直流电机的 PID 控制器
PID概述
在此项目中,我们将实现一个 PID 控制器,该控制器根据编码器提供的速度反馈调整电机的 PWM 信号。为此,需要以下组件。
PID控制器概述
PID 控制器使用三个组件来调节电机速度:
比例 (P):对当前速度误差(期望速度与实际速度之间的差异)做出反应。
积分 (I):考虑过去错误的累积。
导数 (D):根据当前的变化率预测未来的误差。
如何使用 Python 模拟直流电机的 PID 控制器
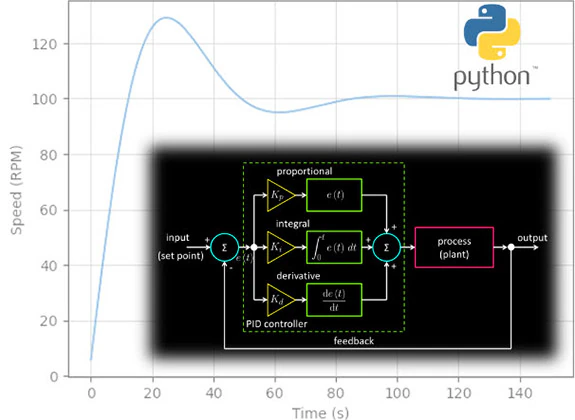
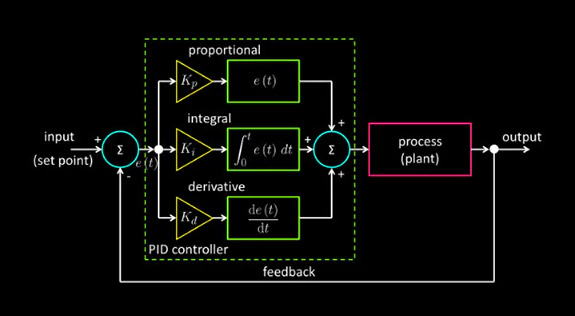
图 1: PID
控制系统框图。
PID控制的公式如下:
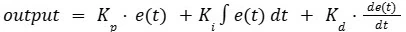
如何使用 Python 模拟直流电机的 PID 控制器
在哪里:
K p、K i和 K d是比例项、积分项和微分项的调整参数。
e(t) 是误差(设定点与当前速度之间的差)。
电机仿真概述
该仿真中使用的电机模型显着简化了实际直流电机的行为。在该模型中,我们假设控制信号和电机速度之间存在直接线性关系,忽略了实际系统中存在的各种复杂性。真实电机会表现出摩擦、惯性和非线性响应,这些在本模拟中均未考虑。电机
电感、反电动势和扭矩-速度关系等因素被忽略,从而降低了模型的准确性。
在现实场景中,由于物理限制,电机的响应会滞后,并且可能不会立即对控制输入做出反应。负载变化和
电源变化等外部因素也可能影响性能。虽然对于理解 PID 控制的基本原理很有用,但这种简化的方法是理想化的,应该通过合并考虑这些物理属性的更详细的模型来扩展现实世界的应用。
代码实现
1. 导入和仿真参数
复制代码
导入matplotlib.pyplot作为plt
导入numpy作为np
我们首先导入必要的库。matplotlib.pyplot用于绘制电机速度随时间变化的曲线,numpy用于生成时间步长数组来模拟时间的流逝。
复制代码
setpoint = 100 # 所需电机速度 (RPM)
Kp = 0.1 # 比例增益
Ki = 0.01 # 积分增益
Kd = 0.05 # 微分增益
dt = 0.1 # 仿真时间步长(秒)
sim_time = 150 # 总仿真时间(秒)
本节初始化模拟的关键参数:
设定点:所需的电机速度(以 RPM 为单位)。
Kp、Ki和Kd:PID 控制器的比例增益、积分增益和微分增益。这些是影响控制器如何响应错误的调整参数。
dt:模拟中每次迭代的时间步长。这是 PID 循环更新的频率。
sim_time:我们运行模拟的总持续时间(以秒为单位)。
2. PID控制器初始化
复制代码
积分= 0
先前错误= 0
motor_speed = 0 # 初始电机速度 (RPM)
# 存储用于绘图的数据
time_data = []
speed_data = []
积分= 0
先前错误= 0
motor_speed = 0 # 初始电机速度 (RPM)
# 存储用于绘图的数据
time_data = []
speed_data = []
积分:积分项随时间累积误差。我们将其初始化为0。
previous_error:跟踪前一个时间步的误差以计算导数项。
motor_speed:电机速度初始设置为 0 RPM(电机从静止状态启动)。
time_data和speed_data:这些列表存储模拟的时间步长和相应的电机速度。它们稍后将用于绘图。
3. 主PID回路
复制代码
for t in np.arange( 0 , sim_time, dt):
# 计算设定值和当前电机速度之间的误差
error = setpoint - motor_speed
该循环针对模拟中的每个时间步运行。 np.arange (0, sim_time, dt)生成从 0 到sim_time的时间步列表,步长为dt。
error:误差是所需速度(设定点)与当前电机速度之间的差异。
4. 比例、积分和导数项
复制代码
# 比例项
P_out = Kp * error
# 积分项(过去误差的累加)
积分 += 误差 * dt
I_out = Ki * 积分
# 微分项(误差变化率)
导数= (误差 - previous_error) / dt
D_out = Kd * 衍生品
比例项(P_out) :该项是比例增益Kp和误差的乘积。它根据当前错误立即做出反应。
积分项 (I_out):误差积分随时间累积,以应对持续的小误差。这是通过将累积误差(积分)乘以积分增益Ki来计算的。误差在累加之前乘以dt,确保其随时间适当缩放。
导数项 (D_out):导数项对误差的变化率做出反应,有助于抑制系统的响应。它的计算方法是用当前误差与之前误差之间的差值除以dt(时间变化)。
5. 控制输出和电机仿真
复制代码
# 计算总控制输出
control_output = P_out + I_out + D_out
# 模拟电机速度响应(简化线性响应)
motor_speed += control_output * dt
control_output:总控制信号是比例、积分和微分输出的总和。这是电机调整速度的输入。
motor_speed:根据控制输出更新电机速度。在这个简化模型中,我们假设电机速度随控制输出随时间线性变化(使用dt调整时间步长)。在真实的系统中,考虑到惯性、摩擦和电气动力学等因素,这会复杂得多。
6. 更新错误和存储数据
复制代码
# 为下迭代更新之前的错误
previous_error = error
# 保存绘图数据
time_data.append(t)
speed_data.append(电机速度)
previous_error:存储当前误差以供下迭代使用,因为在下一个时间步中计算导数项将需要它。
time_data.append(t)和speed_data.append(motor_speed):当前时间和电机速度附加到各自的列表中,该列表将用于在模拟结束时绘制电机速度随时间的变化。
7. 绘制结果
复制代码
#绘制 电机 速度 随时间变化的图plt .plot (time_data, speed_data)
plt .title ( '采用 PID 控制的直流电机速度' )
plt .xlabel ( '时间 (s)' ) plt
.ylabel ( '速度 (RPM)' )
plt .grid (真)
plt .show ()
仿真循环完成后,我们使用matplotlib绘制电机速度随时间变化的图。
plt.plot(time_data, speed_data) :这将创建电机速度 ( speed_data ) 与时间 ( time_data )的线图。
plt.title()、plt.xlabel()、plt.ylabel()和plt.grid()用于向绘图添加标签和网格,使其更易于阅读。
,plt.show()显示绘图。
解释结果
结果如图 1 所示,描述了在代码中实现的 PID 控制下直流电机速度随时间的变化。电机速度首先快速增加,在 120 RPM 左右达到峰值,这表示由于设定值 (100 RPM) 和电机启动速度 (0 RPM) 之间的初始误差较大而导致的过冲。这种超调是由于控制器中比例项和积分项的综合影响而发生的。
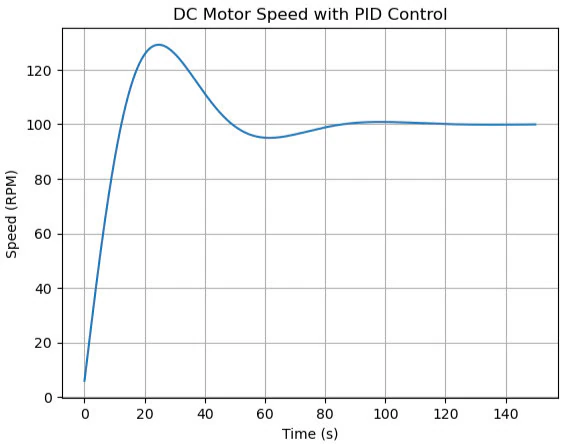
图 2:PID 控制下直流电机速度随时间的变化。
峰值之后,速度随着误差的减小而减小,并且微分项会抑制响应,导致下冲低于设定值。然后系统会轻微振荡,然后稳定在 100 RPM 的所需速度,这反映了 PID 控制器尝试动态纠正误差。
过冲、下冲和逐渐稳定行为是 PID 控制系统的典型行为。由于所有三个 PID 项的联合作用,电机终稳定在设定点附近,可能需要进行一些微调才能更快地收敛。
调整 PID 控制器
PID 控制器的性能在很大程度上取决于您如何调整增益(Kp、Ki、Kd)。这是一般准则:
增加 Kp 可使系统响应更快,但要注意是否出现超调。
增加 Ki以消除稳态误差,但要小心积分饱和,这可能会导致不稳定。
增加 Kd可通过减少振荡来平滑响应,但过多会导致响应缓慢。