正弦波,也称为正弦正弦波或正弦波形,是一种平滑的周期性振荡,描述了空间或时间上的重复模式。它是电气工程中简单且使用广泛的波形类型之一。正弦波是周期性存在于“时域”中的。因此,它们可用于分析线性电气系统在特定频率范围内的频率和/或相位响应。
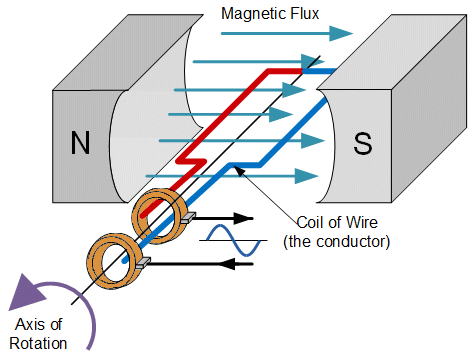
正弦波形通常由旋转
交流发电机或交流发
电机通过电磁感应产生。如果我们在均匀磁场内以恒定速度旋转单个
线圈,产生的电压将采取典型的正弦波形式。因此,在任何时刻,由该旋转动作产生的电压将取决于线圈导体和磁力线之间的关系。
例如,如果线圈平行于磁力线移动,则几乎没有力线被切割,并且产生的电压将为零。同样,如果线圈垂直于磁力线移动,则在该瞬时时间段内将切割数量的磁通线,从而产生电压。
磁场正弦波生成
正弦波产生
因此,线圈在均匀磁场内的恒定旋转导致链接线圈的磁通量的连续变化。当线圈旋转时,此动作会在线圈中产生正弦波电压。
因此,随着线圈旋转,正弦电压(或电流)不仅会定期改变方向,而且幅度也会不断变化。然而,这种周期性波形仅在线圈旋转时存在。
由于生成的电压波形随时间呈正弦变化,因此它将具有与之相关的各种参数,可用于描述它,例如:
正弦波的特征:
幅度 (A): 原点(正弦波的高度)上方的位移,正或负。
周期(T): 波形完成一个完整周期所需的时间。
频率 (f): 每秒重复的次数。频率是周期的倒数 (f = 1/T)。
相位 (θ): 沿水平轴的偏移,确定正弦波的起始位置。
因此我们可以看到,正弦波是一种随时间变化的信号,它产生定义所生成信号形状的“正弦波形”。正弦波形的瞬时值作为时间的函数可以用以下正弦波方程表示:
a (t) = Asin(θ)
即,瞬时值a (t)等于值乘以时间角的正弦。
这种广义的数学表示描述了正弦波随时间的生成,但这意味着什么呢?作为周期性波形,正弦波也可以使用数学三角函数来创建,这些三角函数以角度的正弦函数或余弦函数表示。
正弦波的数学表示
三角函数、正弦和余弦是周期函数,因此我们可以使用它们来定义单位圆周围点的坐标。
基本上,单位圆定义为单位半径 (r = 1) 的圆,其中心位于穿过它的水平(实)线段和垂直(虚)线段的交点。单位半径有一个可变角度θ(theta),可以绕完整的360 °圆周旋转。一般来说,theta 是从正实轴逆时针方向测量的,如图所示。
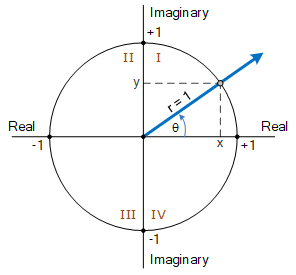
正弦波单位圆
正弦波单位圆
由于圆的周长 (C) 是 π (pi) 与其直径 D 的乘积。用于确定圆的周长的标准数学公式简单地给出为:C = πD。
然而,圆的直径 (D) 也是其半径 (r) 的两倍,因为半径的长度是直径长度的一半。因此D = 2r。那么我们可以正确地说:
C = πD = π2r或C = 2πr
因此,如果一个单位圆的半径等于 1 (r = 1),则其周长为 2π。换句话说,绕单位圆的圆周旋转 1 整圈,其长度等于 2π 单位。
我们在学生时代也知道,绕一圈旋转一周的长度据说为 360 度 (360 o )。那么围绕单位圆的圆周每转一圈的距离等于 360 o或 2π。但如果单位圆的周长可以等分为360度,那么2π用什么单位来表示呢?
正弦波的弧度测量
还有另一种角度测量单位,称为弧度。弧度(rad)是圆的两个半径之间的圆心角,以长度等于半径的弧线切割圆的圆周。那么角度的测量值为 1 弧度,如图所示。
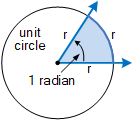
正弦波的弧度
显然,在考虑单位圆时,度数和弧度之间必定存在关系,而且确实存在这种关系。
如果半径为“r”的圆的周长等于:2πr。那么在一个完整的单位圆内必须有 2πr/r = 2π 弧度。现在,由于整圆也有 360 度,这给了我们弧度与度数的比率。 2π 到 360 o,或者 π 到 180 o表示半圆。这给我们提供了以下关系:
1弧度= 360 度 ÷ 2π = 57.296 角度
我们可以从 θ = 0 o到 θ = 360 o (一个整圆)以 15 o间隔(或任何您想要的值)的不同步长创建角度值表,将每个角度从度数转换为弧度,如图所示。
度数到弧度表
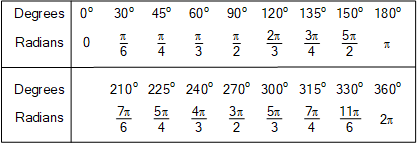
度数与弧度的换算表
确定圆的周长 (C) 后,可以将其分为度数或弧度 (rad) 的角度测量值。如果我们将单位圆的周长展开成一条等长的直线。现在,我们有了用于构造正弦波波形的水平 x 轴的基础,如图所示。
正弦波波形的水平轴
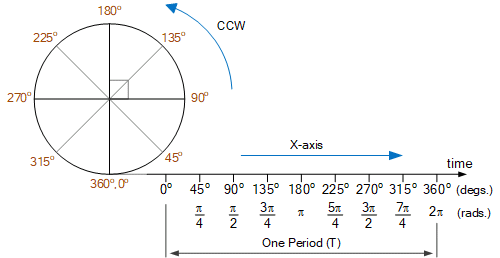
正弦波水平轴
然后我们可以看到,将圆逆时针方向旋转一整圈直到与自身重合所形成的角度为 360 度。因此,1 度 1 o等于 1/360 转。因此,90 °的直角将代表一圈的 1/4,而 180 °的直角将代表一圈的 1/2。
显然,如果我们继续第二次或第三次旋转圆,我们将为水平 x 轴重复相同的序列。因此我们可以看到,该函数将是周期性的,周期 (T) 为 2π,一旦我们知道一段长度间隔内的轴值,我们就会知道所有以度或弧度为单位的值。
正弦波的三角函数
好的,现在我们了解了正弦波的水平 x 轴如何以及为何以度或弧度 (rad) 为单位,现在我们可以使用三角学来构造垂直 y 轴来表示波形幅度。
三角学是对三角形的边和角之间存在的关系的研究。因此,我们可以使用直角三角形以图形方式创建正弦波的波形,说明此概念的一种方法是使用矢量。
矢量是一条线,指示空间中点的大小和方向。大小由其长度表示,方向由其旋转
角度表示。但要做到这一点,我们需要一种表示向量的代数方法。对我们来说幸运的是,毕达哥拉斯定理就是关于找到直角三角形的角和边。
毕达哥拉斯定理在定义和理解正弦波的构造方面发挥着关键作用,特别是在三角学中单位圆的背景下。正弦函数和直角三角形之间的关系可用于可视化和定义沿水平轴的正弦波。