RC 微分器公式

然后我们可以看到输出电压 V OUT是输入电压 V IN的导数,它由 RC 常数加权。其中 RC 表示串联电路的时间常数τ 。
当单步电压脉冲首先施加到 RC 微分器的输入时,电容器初“出现”为快速变化信号的短路。这是因为方波正向边沿的斜率 dv/dt 非常大(理想情况下是无穷大),因此在信号出现的瞬间,所有输入电压都会传递到电阻两端出现的输出。

充电
电容电压
输入信号的初始正向边沿过去且输入峰值恒定后,电容器开始以正常方式通过
电阻器充电,以响应输入脉冲,充电速率由 RC 时间确定常数,τ = RC。
随着电容器充电,电阻器两端的电压,因此输出以指数方式下降,直到电容器在 5RC (5T) 时间常数后完全充电,导致电阻器两端的输出为零。因此,充满电的电容器两端的电压等于输入脉冲的值,如下所示:V C = V IN并且只要输入脉冲的幅度不改变,该条件就成立。
如果现在输入脉冲发生变化并返回到零,则脉冲下降沿的变化率会通过电容器传递到输出,因为电容器无法响应这种高 dv/dt 变化。结果是输出出现负向尖峰。
放电电容电压
在输入信号的初始负沿之后,电容器恢复并开始正常放电,电阻器两端的输出电压以及输出随着电容器放电开始呈指数增加。
因此,每当输入信号快速变化时,输出端就会产生一个电压尖峰,该电压尖峰的极性取决于输入是正向还是负向变化,因为正向尖峰是随着正向信号产生的。输入信号的边沿,以及负向输入信号产生的负尖峰。

因此,RC 微分器输出实际上是输入信号变化率的图表,它与方波输入波没有相似之处,但在输入脉冲改变值时由窄的正负尖峰组成。
通过改变方波输入脉冲相对于串联组合的固定 RC 时间常数的时间周期 T,输出脉冲的形状将发生变化,如图所示。
RC 微分器输出波形
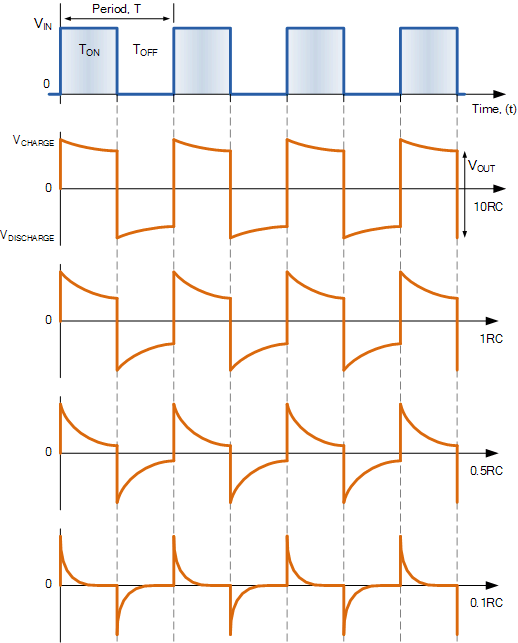
rc 微分器输出波形
然后我们可以看到,输出波形的形状取决于脉冲宽度与 RC 时间常数的比率。当 RC 比脉冲宽度大得多(大于 10RC)时,输出波形类似于输入信号的方波。当 RC 远小于脉冲宽度(小于 0.1RC)时,输出波形呈现非常尖锐且窄的尖峰形式,如上所示。
因此,通过将电路的时间常数从 10RC 更改为 0.1RC,我们可以产生一系列不同的波形。通常,RC 微分器电路中总是使用较小的时间常数,以便在 R 上的输出端提供良好的尖脉冲。因此,方波脉冲(高 dv/dt 阶跃输入)的微分是无限短的尖峰,从而导致 RC 微分器电路。
假设方波波形的周期 T 为
20mS,脉冲宽度为 10mS(20mS 除以 2)。为了使尖峰放电至其初始值的 37%,脉冲宽度必须等于 RC 时间常数,即 RC = 10mS。如果我们选择电容 C 值为 1uF,则 R 等于 10kΩ。
为了使输出与输入相似,我们需要 RC 为脉冲宽度值的十倍 (10RC),因此对于 1uF 的电容器值,这将给出一个电阻值:100kΩ。同样,为了使输出类似于尖锐脉冲,我们需要 RC 为脉冲宽度的十分之一 (0.1RC),因此对于相同的 1uF 电容值,这将给出一个电阻值:1kΩ,依此类推。
RC 微分器示例

rc 微分器示例
因此,通过使 RC 值为脉冲宽度的十分之一(在上面的示例中为 0.1 x 10mS = 1mS)或更低,我们可以在输出处产生所需的尖峰,并且对于给定脉冲宽度,RC 时间常数越低,尖峰越尖锐。因此,输出波形的确切形状取决于 RC 时间常数的值。




