稳态电流和电流密度

 　电流

　　我们可以将电导体想象为自由电子电荷的储存库，在施加场的影响下很容易移动。图 1(a)显示了一个隔离的铜线导电环路。该环路处于静电平衡状态，内部或沿其表面不存在电场。尽管存在自由电子，但没有净电力作用于它们，因此不存在电流。而且，铜线的所有点都处于相同的电位。

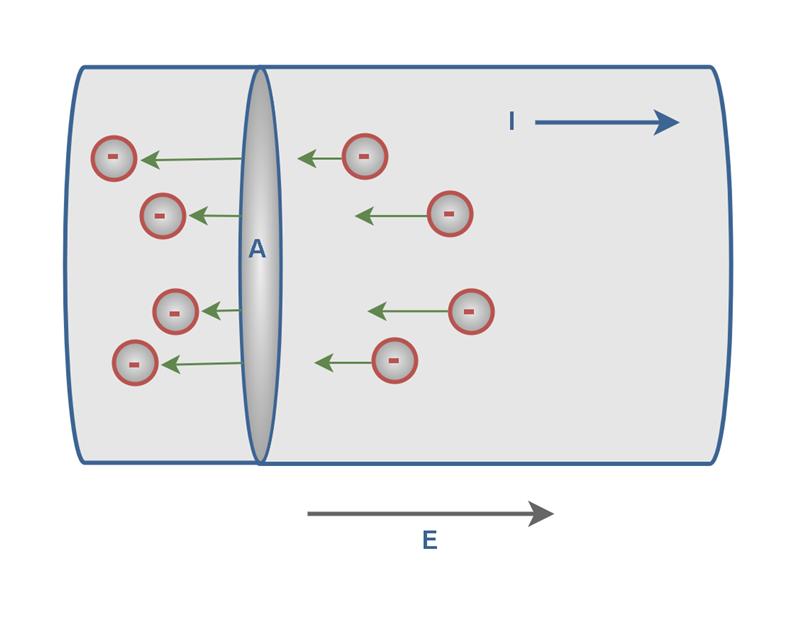
　　图 1：(a) 处于静电平衡状态的铜环 (b) 插入环中的电池图 1：(a) 处于静电平衡状态的铜环 (b) 插入环中的电池通常，一段孤立的铜线中的自由电子以非常高的速度进行随机运动。如果我们通过这样一根导线（如图 1(a)中的平面 cc' 所示）穿过一个假设的横截面，这些电子会以每秒数十亿的速率在两个方向上穿过它，但没有净传输充电，因此电线中没有电流。如果如图 1(b)所示，我们在回路中插入电池，则导电回路将不再处于单一电位。连接到电池正极和负极端子的回路两端之间存在电势差。本质上，这种配置是具有恒压源或电源的闭合电路。因此，电池在环路内产生从正极端子到负极端子的电场。电场对传导电子施加力，使它们移动，从而建立电子流。这意味着，通过将电线的末端连接到电池，我们可以稍微偏向一个方向的电子流，从而产生电荷的净传输，从而产生通过电线的电流。经过很短的时间后，电子流达到恒定值，电流不随时间变化。这意味着电流处于稳态条件。一般来说，电流是移动电荷流。然而，并非所有移动电荷都会形成电流。如果有电流通过给定表面（如图 1(b) 中的平面 cc'）， 则必须有净电荷流过该表面。图2显示了电荷在垂直于区域A的表面的方向上移动。例如，该区域可以是电线的横截面积。电流是电荷流过该表面的速率。

　　图 2：电荷（电流 I）流经导体中的区域 A

　　电流用“I”表示。假设 ΔQ 是在时间间隔 Δt 内流经区域 A 的电荷量，并且流动方向垂直于该区域。那么平均电流 I av等于电荷量除以时间间隔，如等式1中所解释的。

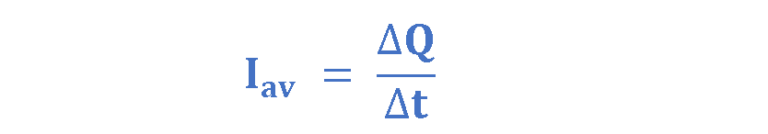
　　方程 1：平均电流的定义

　　电流的 SI 单位是库仑每秒或安培( A )。它以法国数学家和物理学家安德烈-马里·安培（André-Marie Ampère，1775-1836）的名字命名。请注意，一安培电流相当于在 1 秒的时间间隔内通过横截面积的一库仑电荷：1 安培 = 1 A = 1 库仑每秒 = 1 C/s。 电流是由单个移动的电荷组成的，因此对于极低的电流，可以想象单个电荷可以在某一时刻通过区域A，而在下一时刻则没有电荷。然而，实际的系统通常涉及大量的费用。因此，定义瞬时电流是有意义的。 瞬时电流“I”是时间间隔接近零时平均电流 (I av )的极限，如等式 2中所解释。它通常也用小写字母“i”表示，或表示为时间相关函数 i(t)。

　　方程2：瞬时电流的定义

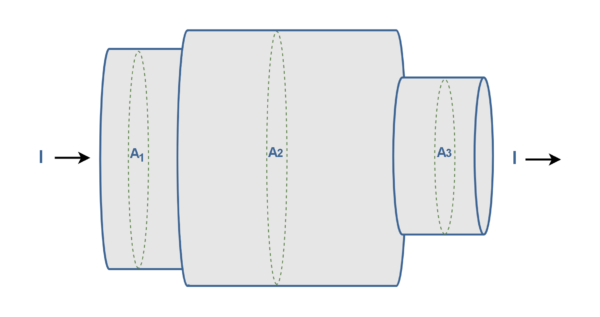
　　当电流稳定时，一段时间内的平均电流和瞬时电流相同（I = I av ）。图 3显示了具有不同横截面（厚度）的导体的纵向切割，其中已建立电流“I”。

　　图3：不同截面积的铜线
　　如果电荷 Δq 在时间 Δt 内穿过假设平面（例如 A 1），则通过该平面的电流 Iav定义为等式 1。在稳态条件下，对于平面 A 1、A 2和 A 3以及实际上对于完全穿过导体的所有平面，电流是相同的，无论它们的位置如何。电流（如公式1所定义）是标量，因为电荷和时间都是标量。然而，如图 1b 所示， 我们经常用箭头表示电流，以指示电荷正在移动。然而，这样的箭头不是矢量。当前的箭头仅显示沿导体的流动方向（或方向），而不是空间方向。
　　电流的方向

　　移动电荷，无论是正电荷还是负电荷，都被称为电荷载流子。例如，在金属中，电荷载流子是电子。在某些情况下（例如气体和电解质），电流是正电荷和负电荷（例如离子）流动的结果。传统上，电流的方向被认为是正电荷从源的正端子流经电路并流入源的负端子的方向。这一历史惯例起源于大约 200 年前，当时引入了正电荷和负电荷的概念。常规电流方向是在电子发现之前建立的，并且仍在电路分析中使用。本质上，在铜等常见导体中，电流的实际方向取决于带负电的电子的运动，如图2所示。然而，电流的常规方向与电子的运动方向相反（参见图2中电流I的方向）。电气工程中的惯例将正电流定义为正电荷从电压源（例如电池）的正极 (+) 端子流向负极 (-) 端子。对于电阻器、电容器或电感器等无源 器件，正电流对应于正电荷流入器件的正电压端子。图 4描述了电气工程和物理学中普遍使用的这一约定。

　　图 4：简单电路中的常规电流
　　该电路演示了电阻器 (R)、电容器 (C) 和电感器 (L) 的并联连接，由电池供电。这种配置在 RLC 电路中很常见，而 RLC 电路是许多电子应用的基础。常规电流“I”从电池的正极开始并通过导线继续移动。然后，它在电阻器 (I R ) 和电容器 ( IC ) 以及电感器 (I L )之间分配。，电流的所有部分结合在一起以重新形成电流“I”，该电流返回到电池的负极性。
　　电流类型
　　在实践中，我们通常处理电流的两种物理机制：传导和对流。传导电流由电荷载流子（通常是电子）响应电场而流过导体组成。图 1b中提到的电流就是这种情况的一个很好的例子。在某些材料中，电场还能够使原子中的弱束缚电子发生位错，然后电子在与其他原子重新结合之前移动一段距离。因此，传导电流中的各个电子不一定行进被认为存在电流的整个距离。对流电流由响应机械力移动的带电粒子组成，而不是由电场引导。它通常是含有带电粒子的流体或气体（如等离子体）的整体运动所携带的电荷流。在某些系统中，除了传导电流之外，它还可以存在。对流的一个例子是带有自由电子的云，它在风的驱动下穿过大气层。对流的其他例子是电解质溶液中的离子流或真空管中的电子束。
　　电流密度

　　从宏观角度来看，电气工程中的许多重要问题都涉及电流流动不以简单方式受到限制的情况。示例包括射频的电线和针式互连、电路板和外壳接地，以及闪电等物理现象。为了适应这类更一般的问题，我们必须将电流定义为向量。此外，这些问题中的电流可以在表面和体积内扩散，因此我们还必须考虑电流的空间分布。在场论中，我们通常对发生在一个点而不是一个大区域内的事件感兴趣，因此我们发现电流密度的概念更有用。想象一下，电流 I 均匀分布在圆柱形导体内，如图 5所示。

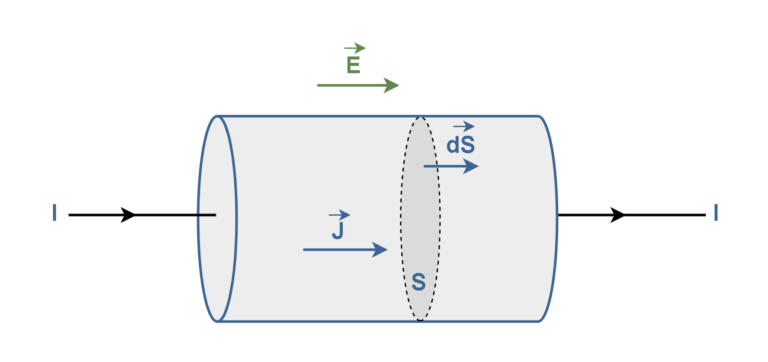
　　图 5：圆形截面导线中的总电流 I 和电流密度 J令“ J ”为称为电流密度的矢量，表示每秒流过单位横截面积的电荷量。还让' dS '是一个向量，表示这个小表面的面积，方向垂直于表面。然后，均匀地流过整个表面“S”的总电流I由等式3中的表面积分来解释。

　　方程 3：基于电流密度的电流定义

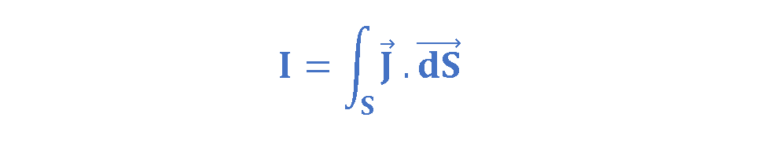
　　其中dS以 m 2为单位测量，J是以安培每 平方米(A/m 2 )为单位测量的表面电流密度，I 是以安培 (A) 为单位的总电流。换句话说，表面S上的电流密度J积分产生通过该表面的总电流“I”。在这个概念中，场论方法可能与电路方法相关。由于宇宙结构的某些对称性，电荷是保守的。这意味着孤立系统的总电荷在所有时间点都保持不变。 “电荷守恒定律”是基本的、严格的和普遍的。因此，如果我们再次参考图3 ，我们可以得出结论，通过表面A 1或A 2或A 3的电荷量随着时间的推移是恒定的，即I = 恒定。然而，电流密度 J 确实发生了变化——在具有较小表面（A 1和 A 3 ）的较窄导体中电流密度 J 较大。图 6显示了电流为 I 0 的导体在结点“a”处分成电流为 I 1和 I 2 的两个分支。

　　图 6：电流的结点规则

　　由于电荷守恒，因此分支中的电流大小必须相加才能产生原始导体中的电流大小，如公式 4所示：

　　公式 4：结点中输入和输出电流之间的关系
　　它只是意味着进入结点（节点）的所有电流之和必须等于离开结点的所有电流之和。电路理论中的这一原理被称为基尔霍夫电流定律（KCL）——结点规则。无论三根导线在空间中的方向如何，方程 4中的电流之间的关系在结点 a 处均成立。这是因为电流是标量，而不是矢量。
　　漂移速度

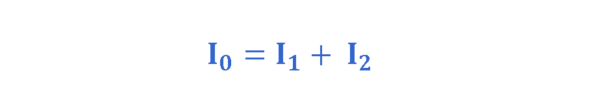
　　金属中的导电现象可以从原子或微观的角度来考虑。对于我们的目的来说，一个简单的物理模型就足够了。我们可以认为导体是由包含自由移动的电子气的固定正离子晶格组成。通常，这些自由电子由于其热能而处于随机运动状态。当导体没有电流通过时，其传导电子会随机移动，没有特定的方向。然而，导体中施加的电场会导致电子沿指定方向漂移。因此，当导体有电流通过时，这些自由电子仍然随机移动，但现在它们倾向于以漂移速度 v d沿与引起电流的外加电场相反的方向漂移。在导体中移动的自由电子与其他电子和原子发生多次碰撞。一个电子的路径如图7所示。

　　图 7：载流导体中负电荷的漂移速度

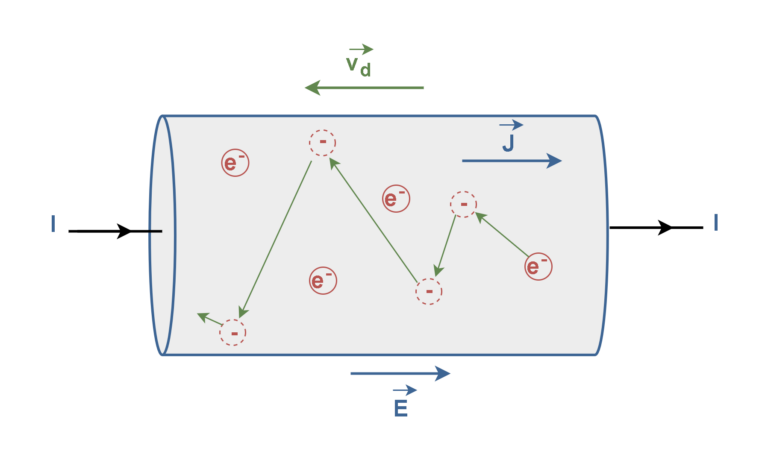
　　本质上，漂移速度是自由电荷的平均速度。图7将通过导线的电流“I”中传导电子的漂移速度“ v d ”与导线中电流密度的大小“ J ”联系起来。它还显示了负电荷载流子在所施加电场“ E ”的相反方向上的漂移。让我们假设这些载流子都以相同的漂移速度v d移动，并且电流密度J在导线的横截面积“S”上是均匀的。然后，可以按照等式5计算电流密度。

　　其中“n”是每单位体积的载流子数量，“e”是一个电子的电荷（以库仑为单位）。乘积“ne”是载流子密度，其SI单位是库仑每立方米(C/m 3 ) 。对于正载流子，矢量J和v d具有相同的方向。对于负载流子，矢量J和v d具有相反的方向。当带电粒子被迫进入导体的这个体积时，相同数量的电荷很快就会被迫离开。相同电荷之间的排斥使得增加体积中的电荷数量变得困难。因此，当一个电荷进入时，另一个电荷几乎立即离开，将信号快速向前传送。与随机运动速度相比，漂移速度很小，随机运动速度通常约为 10 6米每秒 (m/s)。例如，在家庭布线的铜导体中，电子漂移速度可能为10 -5至10 -4 m/s。由于有如此多的自由电荷，漂移速度非常小。如果我们估计导体中自由电子的密度，我们就可以计算给定电流的漂移速度。密度越大，给定电流所需的速度越低。