频率密度和噪声
在上一篇文章中,我们考虑了一个简单的情况:调幅正弦信号。执行采样/截断后,很容易确定傅里叶频谱中是否存在单个频率:正弦振荡的频率。对于更复杂的过程,预计会出现更多的频率。问题是:“从存在无限频率的意义上来说,是否存在傅里叶频谱无限密集的信号/过程?”
乍一看,这似乎是一个病态病例的存在;但事实上,这似乎是一个病态病例的存在。事实上,这些过程非常普遍:我们正在谈论噪音。例如,图 1 显示了白噪声的典型傅里叶频谱(方差为 1,平均值为零)。与往常一样,重要频谱从采样索引的 0 延伸到 1,000(不要与频率值混淆):频谱的第二部分是部分的复制品。
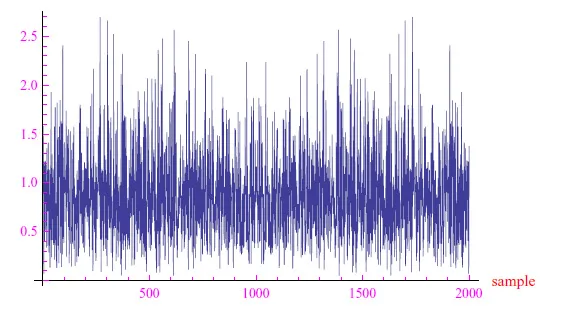
图 1:白噪声的傅里叶频谱。
图 1:白噪声的傅里叶频谱
统计分析——平稳性和遍历性
白噪声很奇特,因为假定作为时间函数的x ( t ) 值 100% 不相关,因此频谱中存在无限频率。从数学上讲,白噪声是一个在每个点都具有有限不连续性的函数,因此具有不可预测性。另一种解决方案是将x ( t ) 表示为非定义的函数,即对于给定时刻t,数量x可以采用多个值。
在这一点上,很明显描述随机过程的获胜策略是使用统计方法。通过考虑所谓的平稳过程可以实现显着的简化:找到给定x值的概率不依赖于时间。下一步将不是考虑单个进程,而是考虑正在检查的进程的大量(多无限)心理副本。如果我们知道概率的解析表达式,我们就可以对x进行统计平均,通常用 x 表示。这种计算避免了确定x的时间平均值的尴尬问题。事实上,根据平均值的定义:

电力
电子科学笔记:噪声和 DFT/FFT
这种计算不切实际,原因有二:
x ( t ) 不是普通意义上的函数
物理上达到极限的操作转化为无限大的观察/测量时间T。
正是这一种情况提供了解决方案:在无限的时间内,该过程会经历所有可能的配置或我们统计样本的所有心理副本。换句话说,我们得出结论:统计平均值 ? x ? 与时间平均值一致(等式 1)。这种性质被称为遍历性:因此,遍历过程表现出这种有趣的性质。从数学上来说,确定给定过程的遍历性是非常困难的。启发式地讲,大多数物理兴趣的随机过程都是遍历的。
自相关函数 – 维纳-辛钦定理
在图 1 中,我们得到了平均值为零的白噪声的傅立叶频谱。为了数学方便起见,我们总是将自己置于这种情况,即如果 x 不为零,我们仍然可以从各种表达式中减去该值以重现先前的情况。由此可见,根据方差的定义,有:σ 2 = x 2 ;但这只不过是总信号强度。现在让我们考虑以下量,其幂次维度为ψ ( τ ) = ? x (0) x ( τ )? 无论τ起到时间变量的作用。很明显,ψ (0) 是方差,而在不同时间,它告诉我们各个值x (0) 和x ( τ ) 如何“相关”。对于白噪声,我们有:

为了表示这样的对象,狄拉克δ函数可以帮助我们:ψ ( τ ) = σ 2 δ ( t ),即使它不能再现需要积分的ψ (0)。众所周知,狄拉克δ的傅里叶变换是一个常数函数,因此(2)的傅里叶变换是“平坦的”,这正是白噪声功率谱的预期,因为每个频率对相同的频率有贡献。信号功率的权重。
这些结论有一个共同特征:它们对于任何遍历过程x ( t ) 都是有效的。称为自相关函数的对象ψ ( τ ) 与x ( t )的功率谱之间的联系构成了的维纳辛钦定理的陈述: x ( t )的自相关函数的傅里叶变换是功率x ( t )的频谱。
Mathematica中的自相关函数
Mathematica提供了模拟白噪声的可能性,然后确定其功率谱和自相关函数。对于这种环境,每条指令都被视为一个“函数”,其参数是模式,因此它们也可以是列表。因此,我们定义了一个 PowerSpectrum[x
List] 函数,其中下划线向Mathematica内核传达 x 可以是任何东西,只要它是一个“列表”。简而言之,x 是时间序列(采样和截断的信号)。然后,代码块内的指令执行傅里叶变换与变换本身的复共轭的乘积(根据功率谱的定义)。
根据维纳辛钦定理,自相关函数是功率谱的逆变换。所以我们定义了一个函数 Correlate[x List]。例如,在白噪声的情况下,我们得到图 2 中的趋势,从中我们可以看到在非零时间不存在相关性。
图 2:均值为零、方差为 1 的白噪声的自相关函数。
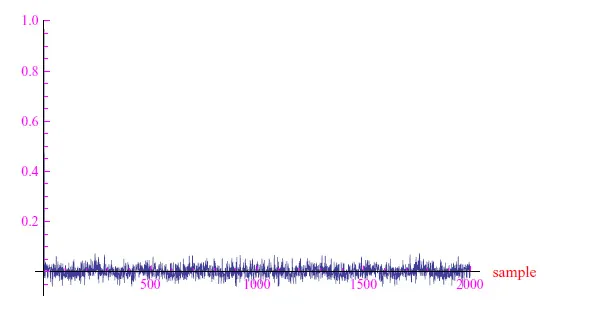
图 2:均值为零、方差为 1 的白噪声的自相关函数
素数的情况
作为 Mathematica 脚本的应用示例,我们研究素数的分布。准确地说,用p n 表示第n个,我们定义序列:

这相当于连续情况下的导数。通过绘制n 1 时的 { δ n }图形,我们获得了白噪声类型的趋势。正如我们从图 3 和图 4 中看到的那样, Giovanni Di Maria在 Octave 中证实了这一点。
因此,素数的分布是白噪声或维纳过程的积分。

图 3:n = 1 时的 {δn} 趋势,..,2000 年(Giovanni Di Maria)。
图 3:n = 1 , .., 2000 时 { δ n }的趋势(Giovanni Di Maria)

图 4:{δn} 的自相关函数(Giovanni Di Maria)。
图 4:{ δ n }的自相关函数(Giovanni Di Maria)






