RTD 信号调节 - 4 线配置、比率测量和滤波

　　RTD 4 线配置 — 压降和开尔文传感
　　下图 1 显示了电流激励 RTD 的四线接线技术。

　　电流激励 RTD 中的四线技术框图。

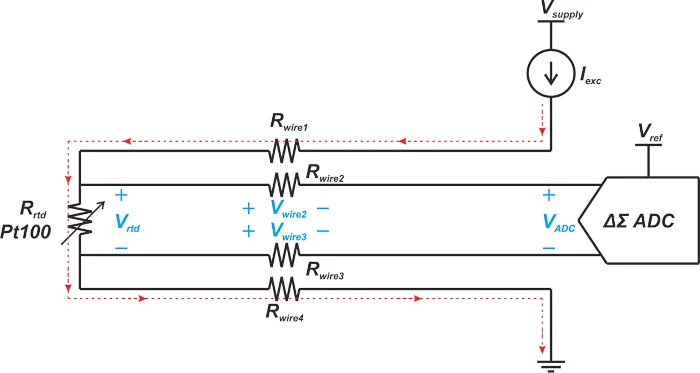
　　图 1. 电流激励 RTD 中的四线技术框图。
　　模数转换器(ADC)输入为高阻抗，这导致激励电流流过 Rwire1 、 R rtd和Rwire4。由于Rwire2和Rwire3上没有电流流过， 因此这两个电阻上没有压降，ADC可以准确测量RTD电压Vrtd。
　　三线配置需要两个匹配的电流源来消除线电阻误差，而四线配置可以通过单个电流源实现这一点。请注意，上述方法也称为开尔文传感，是一种通用电阻测量技术，可用于许多其他领域，例如电阻电流传感 应用。
　　四线测量概念也可应用于电压激励 RTD，如图 2 所示。

　　显示电压激励 RTD 中的四线测量概念的框图。

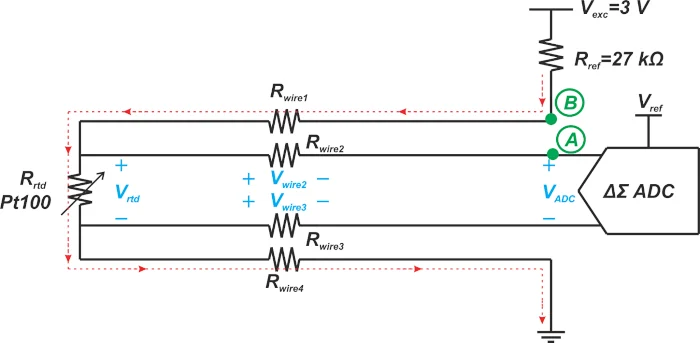
　　图 2. 显示电压激励 RTD 中四线测量概念的框图。
　　同样，R线 2 和 R线 3上没有压降，并且 ADC 准确测量 RTD 上的电压 V rtd。在电压励磁系统中，励磁电压 V exc 是已知的。然而，不可能通过知道V rtd 和V exc来确定RTD 电阻，因为一些未知的电压也会在R线1 和R线4 上下降。为了解决这个问题，我们可以在节点（例如上图中的节点 B）进行额外的测量，以计算出流过传感器的电流。这与我们在上一篇文章中讨论电压激励三线配置时使用的方法类似。
　　请注意，对于电流激励，不需要第二次测量，因为流过传感器的电流 I exc是已知的。电流激励方法是一种更直接的实现方式，特别是当导线电阻误差成为问题时。
　　比例测量基础知识
　　所有 RTD 测量电路都需要准确且稳定的激励源，因为 RTD 电压是激励源的函数。例如，考虑图 1 中的电路图。ADC 测量的电压与 RTD 电阻的关系如下：

　VADC=Rrtd×Iexc　

　如果激励电流存在噪声或随温度或时间漂移，则即使温度固定，RTD 两端的电压也会发生变化。为了保持高精度，设计人员需要使用精密元件来限度地减少 I exc的变化。

　　或者，您可以使用比率测量。比率测量不是化激励源变化，而是改变电路，使输出与 I exc 与系统中另一个电流（或电压）的比率成正比。
　　假设电路经过修改，输出方程变为：
　　VADC=Rrtd×IexcIx
　　其中 I x 是电路中的电流。另外，如果我们 从 I exc导出 I x  ，并且它们都经历相同的变化，则比率
　　 IexcIxIexcIx 　　可以保持恒定。这使得测量系统对激励源的变化不敏感。
　　在下一节中，我们将看到比率测量通常可以以较低的成本实现。这种廉价的实现方式使我们能够使用比例配置来提高精度并放宽某些组件（例如激励电压或电流源）的要求。

　　比例 RTD 测量

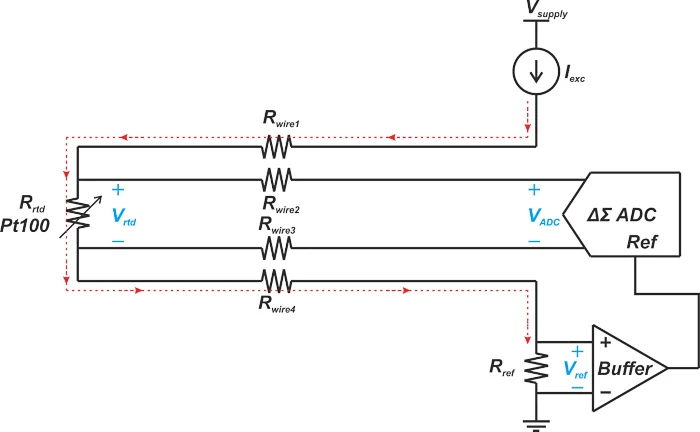
　　图 3 显示了如何修改四线电流激励测量以具有比率配置。
　　显示四线电流激励测量的框图可以修改为具有比率配置。
　　图 3. 显示四线电流激励测量的框图，可以修改为具有比例配置。
　　在这种情况下，激励电流通过精密参考电阻 R ref 以创建 ADC 参考电压。缓冲器用于感测 R ref两端的电压 ，而不对该电阻器造成任何负载影响。虽然缓冲器显示为外部组件，但它通常集成到ADC芯片中，并且不需要外部缓冲器。
　　从这里，让我们看看上述电路如何产生比率测量。ADC 输入电压和参考电压由以下等式给出：

　

VADC=Rrtd×IexcVADC=Rrtd×Iexc

等式 1。

Vref=Rref×IexcVref=Rref×Iexc

等式2。

　　n 位 ADC 产生的数字输出通常可以用以下等式描述：

　　数字值=模拟输入电压ADC参考电压×(2n?1)　

  　ADC 输出与输入电压与其参考电压的比率成正比。将式1和式2代入上式，可得：

　数字值=Rrtd×IexcRref×Iexc×(2n?1)　　

   这简化为：

　 数字值=RrtdRref×(2n?1)　

 　ADC 输出不再是激励电流的函数。然而，R ref 应该是低容差和低漂移电阻器，因为 R ref中任何不需要的变化 都会直接转化为测量结果中的误差。图 4 显示了三线 RTD 应用的比例配置。

　　三线 RTD 应用的比率配置示例。

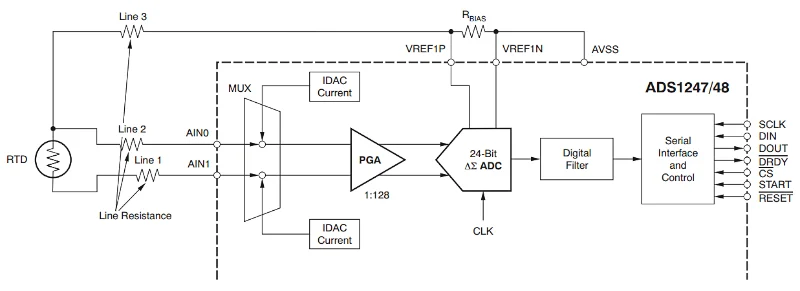
　　图 4. 三线 RTD 应用的比率配置示例。图片由TI提供
　　比例测量概念也可应用于电压激励 RTD。图 5 显示了一个示例。

　　电压激励 RTD 的比率测量框图示例。

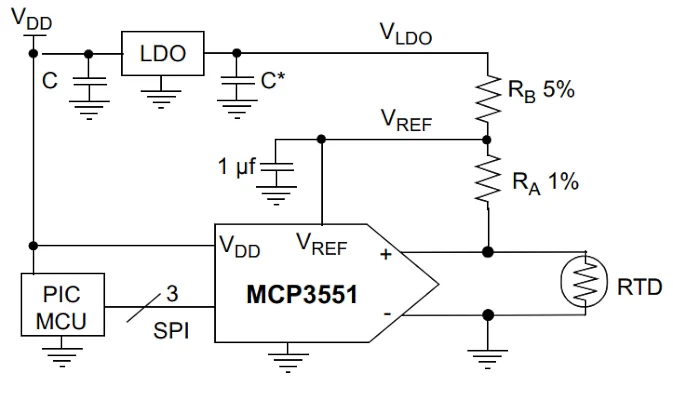
　　图 5. 电压激励 RTD 的比率测量框图示例。图片由Microchip提供
　　上图使用与 ADC 参考电压和 RTD 激励信号相同的电压。
　　在比例配置中使用 RC 低通滤波器
　　为了衰减来自激励电流和环境的噪声，在比例系统的 ADC 输入和参考路径上放置了RC低通滤波器。图 6 对此进行了说明。

　　在比例系统的 ADC 输入和参考路径上使用 RC 低通滤波器。

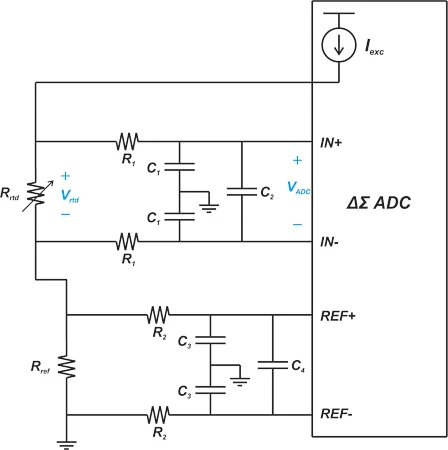
　　图 6. 在比例系统的 ADC 输入和参考路径上使用 RC 低通滤波器。
　　比例电路无需使用外部RC滤波器即可工作；然而，添加低通RC滤波器可以提高电路对射频干扰(RFI)和电磁干扰(EMI)的抗扰度。通过检查图 7a 和 7b 中的电路图可以了解滤波器对共模噪声的响应。

　　显示共模噪声滤波器响应的示例图。

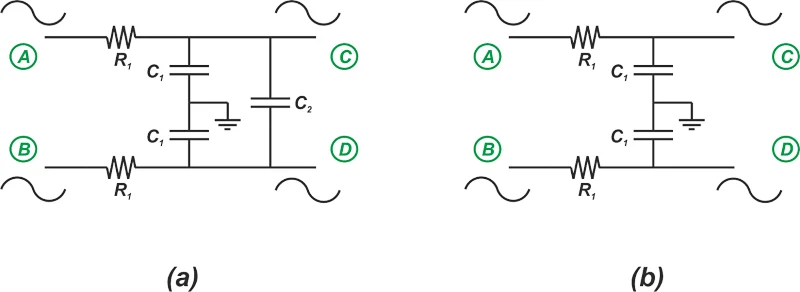
　　图 7. 显示共模噪声滤波器响应的示例图。
　　如图 7(a) 所示，在共模输入下，节点 C 和 D 具有相同的电位。因此，没有电流流过C 2 ， 并且可以从电路模型中移除该电容器。这意味着 C 1 电容器决定共模截止频率，从而得出公式 3：

　f = 1 2 π R 1 C 1　

  　等式 3。

　　另一方面，对于差分输入，C 2可以用串联的两个2C 2 电容器代替，如图8(b)所示。
　　串联连接图示例。

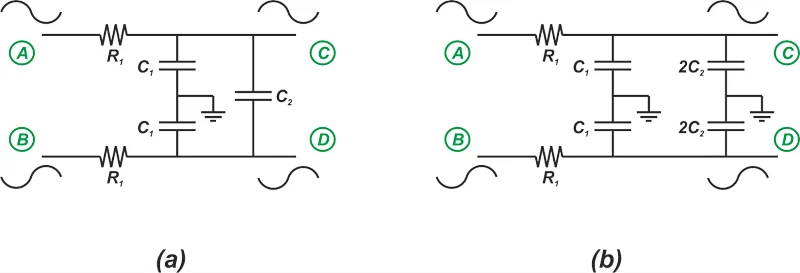
　　图 8. 串联连接图示例。
　　因此，差分截止频率可表示为：

　f = 1 2 π R 1 ( C 1 + 2 C 2 )　

  　等式 4。

　　另外，图 7(b) 显示节点 C 和 D 的共模截止频率分别由上部和下部 C 1 电容器决定。这两个电容器之间的不匹配可能导致两个路径的截止频率之间的不匹配。通过这两个滤波器的不等衰减，共模噪声会在滤波器输出处产生差分噪声，这是完全不希望的。
　　为了抑制共模电容失配产生的差分噪声，建议差分电容C 2 至少比共模电容C 1大10倍。换句话说，差分电容器减少了共模和差分噪声分量。
　　设计这些简单的 RC 滤波器时应考虑几个权衡因素。关于选择滤波器组件以平衡这些权衡的彻底讨论不是本文的目标。然而，需要强调关于比率测量的一个重要点：滤波器匹配对比率系统噪声性能的影响。
　　匹配滤波提高噪声性能
　　在上一节中，我们讨论了每个滤波器内 C 1 电容器的不匹配可能会导致问题（因此，我们向每个滤波器添加了一个差分电容器）。输入和参考路径过滤器之间不匹配怎么办？要回答这个问题，请注意比率系统试图使测量对激励源变化不敏感。仅当激励源变化对 ADC 模拟输入（IN+ 和 IN-）和参考输入（REF+ 和 REF-）具有相同影响时，才能实现这一点。输入路径和参考路径的截止频率之间的不匹配可能导致激励噪声的衰减不均匀，并降低比率配置的有效性。
　　剩下的问题是：什么元件值可以确保滤波器具有相同的截止频率？根据公式 3 和 4，Analog Devices 的另一份 应用笔记 建议对输入和参考路径使用相同的滤波器。该应用笔记还提供了图 9 所示电路图的一些测试结果。

　　应用笔记图示例。

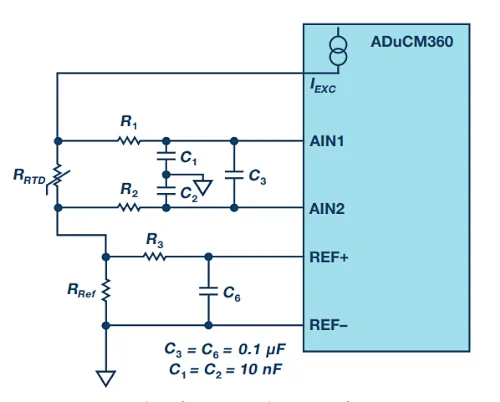
　　图 9. 示例应用注释图。图片由Analog Devices提供
　　需要注意的是，与图6中的一般电路相比，上述电路的参考路径中取消了一个电阻和两个电容。这是因为在本设计中 REF- 引脚接地。该电路的测试结果如表1所示。

　　表 1.使用的数据由Analog Devices 提供

　　该测试使用 100 Ω 精密电阻代替 RTD，并测量 ADC 输入引脚处的噪声电压。R Ref的值为 5.62 kΩ。当两个滤波器相同时（R 1  = R 2  = R 3  = 1 kΩ），与 R 1  = R 2  = 10 kΩ 且 R 3  =不匹配的情况相比，噪声电压降低了约 0.1 V 至 0.3 V 1kΩ。在上面的示例中，相同的 RC 滤波器可以改善噪声性能，但这不一定是可实现的噪声性能。这将在下一节中讨论。
　　改善电流源噪声消除
　　例如，德州仪器 (TI) 的一份应用笔记讨论了输入和参考路径上的相同滤波器不会地消除电流源噪声。在推导等式 3 和 4 时，我们假设滤波器输入（节点 A 和 B）处出现共模或差分噪声。
　　这种类型的分析在概念上类似于将电压源施加到节点 A 和 B 以对输入噪声进行建模。 通过此分析，不考虑与滤波器并联的R rtd 和 R ref电阻器的影响。这两个电阻实际上修改了 RC 网络的时间常数。由于 R rtd 和 R ref 不相等，因此相同的滤波器不能具有相同的截止频率。我上面提到的 TI 文档建议使用零值时间常数技术来推导两个滤波器的截止频率方程。
　　零值时间常数是一种估计系统带宽的方法。对于零值时间常数分析，在信号源设置为零（激励电流用开路代替）时确定每个电容器“看到”的电阻，并用开路代替其余电容器。这种方法之所以被称为 零值 时间常数，是因为除了感兴趣的电容器之外的所有电容器都被设置为零来执行计算。如果电路有 m 个电容器，并且给定电容器 C j的电阻 为 $$R^0_j$$，则系统的 -3 dB 带宽可估计为：
　　? 3 d B = 1 Σ m j = 1 R 0 j C j
　　等式 5。
　　例如，为了确定图 6 中 C 2  和 C 4 电容器两端的电阻，我们分别获得图 10(a) 和 (b) 中的电路图。

　　显示 C2 (a) 和 C4 (b) 电容器两端电阻的图表

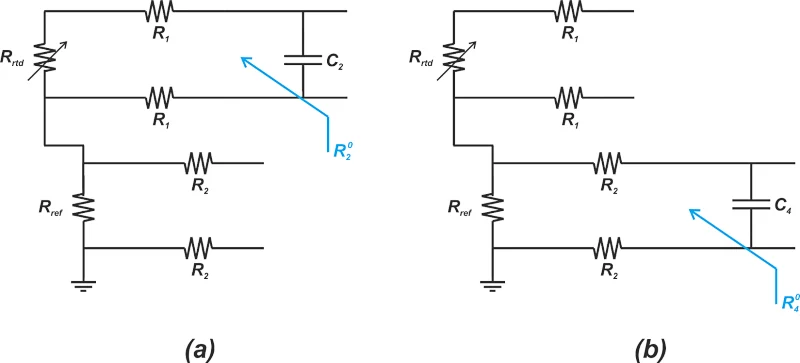
　　图 10. 显示 C 2  (a) 和 C 4  (b) 电容器两端电阻的图表
　　等式 6 和 7 分别显示与 C 2 和 C 4相关的零值时间常数 (ZVT) ：
　　Z
　　V

Z V T 2 = C 2 ( 2 R 1 + R r t d )ZVT2=C2(2R1+Rrtd)

等式 6。

 

$${\mathrm{ZVT}4}_{}=C_{}{}_4(2R_2+R_{\mathrm{ref}}){\_}^{}{}_{\mathrm{\_}}{}_{\_}{}_{\_}$$  

等式 7。

　　等式 7。
　　初，开发零值时间常数方法是为了估计电路的-3 dB 带宽。为此，我们计算电路中所有电容器的时间常数，然后将它们代入公式 5。但是，每个单独时间常数的公式显示了特定电容器如何与其周围的电阻器相互作用以贡献电路带宽。
　　回到我们的 RTD 测量系统，如果三个电容器的零值时间常数相同，则输入和参考路径将具有相同的带宽。因此，ZVT 2  = ZVT 4，从而得出以下等式：

C 2 ( 2 R 1 + R r t d ) = C 4 ( 2 R 2 + R ref ) _ _C2(2R1+Rrtd)=C4(2R2+Rref)

方程 8.

 

　　_
　　方程 8.

　　如果C 2  = C 4 ，则应 适当选择R 1 和R 2电阻器以产生相同的时间常数。根据上述讨论，TI 应用笔记建议使用图 11 中的示例图。

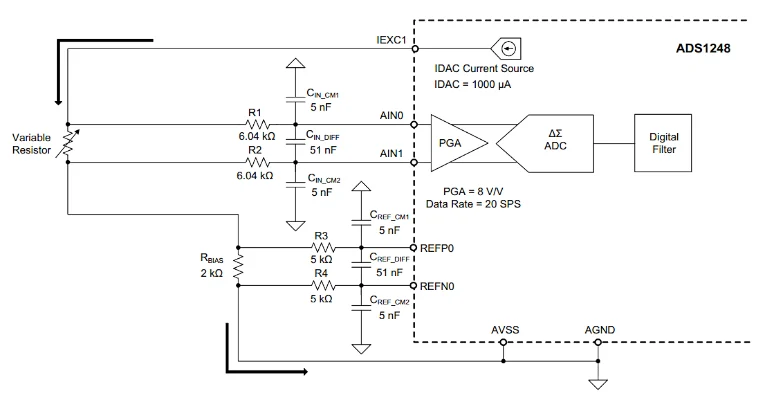
　　ADS1248 的示例框图。
　　图 11.ADS1248 的示例框图。图片由TI提供
　　假设传感器电阻从 0 变化到 250 Ω。由于传感器电阻的变化会改变电路时间常数（公式 6），因此输入滤波器使用相对较大的电阻（R 1  = R 2  = 6.04 kΩ）。这使得 RTD 变化对输入滤波器频率响应的影响微不足道。
　　根据 Analog Devices 的文章，参考路径中使用的电阻应为 6.04 kΩ。然而，TI 设计建议使用 5 kΩ 电阻器来匹配两个滤波器的带宽。图 12 显示了系统的输入参考噪声如何随输入电压电平（即 RTD 两端的电压）变化。

　　显示输入参考噪声与输入电压的关系图。

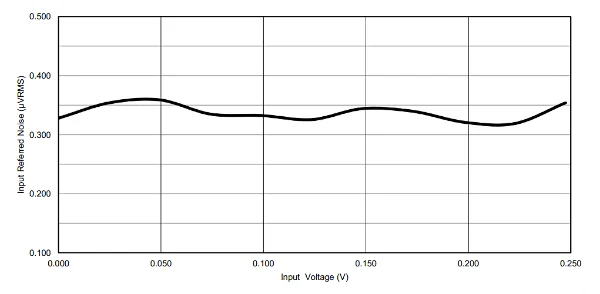
　　图 12. 显示输入参考噪声与输入电压的关系图。图片由TI提供