多速率DSP及其在数模转换中的应用

时间：2023-06-12

理想DAC的概念操作

如图1所示，理想的D/A转换器接收一系列量化值y（n） $y （ n ）$ ，并生成加权脉冲序列 $y_{s} （ t ）$ $。如图 1 中的 $y （ n ）$ 图形所示， $y （ n ）$ 是一个离散的值序列。我们知道特定 $n$ 的 $y （ n ）$ 值，但该图没有提供有关对基础连续时间信号进行采样的采样率的任何信息。D/A 阶段需要知道采样周期 $T$ ，以产生对应于 $y （ n ）$ 时特定值 $n T$ 的脉冲。

图 1.理想 D/A 转换器的操作。图片由数字信号处理提供。

假设 $y (n)$ 的每个值由 $m$ 位表示， $y_{m ? 1} y_{m ? 2} \dots y_{0}$ ，转换器是二进制加权的。因此，我们有

$y_{s} (n T) = \sum_{k = 0}^{m ? 1} y_{k} 2^{k} R_{r e f}$

其中 $R_{r e f}$ 是参考电压、电流或电荷。到目前为止，我们理想的 D/A 阶段已将离散时间量化序列 $y (n)$ 转换为连续时间模拟信号 $y_{s} (t)$ 。

为什么我们在 DAC 之后需要重建滤波器？

$y_{s} (t)$ 等于潜在的连续时间信号， $y_{c} (t)$ , 仅在 $t = n T$ , 否则为零。怎样才能恢复原状 $y_{c} (t)$ 从 $y_{s} (t)$ ？假使，假设 $y (n)$ 是通过对原始信号进行采样得到的， $y_{c} (t)$ , 采样周期为 $T$ .因此，

$y_{s} (t) = y_{c} (t) \times \sum_{n = ? \infty}^{+ \infty} δ (t ? n T)$

在之前的文章中，我们了解了将连续时间信号 $$y_c(t)$$ 与周期为 $$T$$ 的脉冲序列相乘如何导致 $$y_c(t)$$ 的频谱复制品$$\frac{2\pi}{T}$$ 的倍数。这就是为什么图 1 中的 $$y_s(t)$$ 不仅包含基础连续时间信号的频谱，还包含其采样频率倍数的副本。这在图 2 中进行了说明。要恢复 $$y_c(t)$$，我们需要去除高频分量。这是通过图 1 中称为重构滤波器的模拟低通滤波器实现的。 $y_{c} (t)$ , 通过周期为脉冲的火车 $T$ 导致光谱的复制品 $y_{c} (t)$ 的倍数 $\frac{2 π}{T}$ .这就是为什么 $y_{s} (t)$ 图 1 中的频谱不仅包含基础连续时间信号的频谱，还包含其在采样频率倍数处的副本。这在图 2 中进行了说明。要恢复 $y_{c} (t)$ ，我们需要去除高频成分。这是通过图 1 中称为重构滤波器的模拟低通滤波器实现的。

图 2.将信号与脉冲序列相乘会导致输入频谱以采样频率 $$\Omega_s$$ 的倍数复制。图片由离散时间信号处理提供。 $Ω_{s}$ .图片由

为了进一步阐明重构滤波器的要求，假设我们使用$$2\Omega_N$$的采样频率对$$y_c(t)$$进行采样，其能量全部低于$$\Omega_N$$，即, $$Y_c(j\Omega)=0$$ 对于 $$| \欧米茄| > \Omega_N$$。在这种情况下，我们需要一个锐利的重建滤波器，它可以传递高达 $$\Omega_N$$ 的频率分量，并消除 $$Y_s(j\Omega)$$ 刚好高于 $$\Omega_N$$ 的不需要的频率分量。由于这种锐利的过滤特性不实用，我们需要改变我们的设计。 $2 Ω_{N}$ 取样 $y_{c} (t)$ , 它的所有能量都低于 $Ω_{N}$ ，那是， $Y_{c} (j Ω) = 0$ 为了 $| Ω | > Ω_{N}$ .在这种情况下，我们需要一个尖锐的重建滤波器，它将频率分量传递到 $Ω_{N}$ 并消除不需要的频率成分 $Y_{s} (j Ω)$ 就在上面 $Ω_{N}$ .由于这种尖锐的过滤特性不实用，我们需要改变我们的设计。

对于给定的 $$Y_c（j\Omega）$$，如果我们增加采样频率，副本将进入更高的频率，并且重建滤波器可以从通带到阻带的过渡更平滑。例如，假设 $$y_c（t）$$ 表示能量在 $$0 的频段内的模拟音乐波形< \frac{|\Omega|}{2 \pi} < 22 kHz$$.如果我们采样 $$y_c（t）$$ 的采样频率比奈奎斯特采样率 $$f_{s， new}=352 kHz$$ 高 $8$$，那么重建滤波器的过渡带将为 $$（\Omega_s - \Omega_N）- \Omega_N=2 \pi \times 308 kHz$$（见图 2）。但是，使用每秒 352，000 美元的样本来表示所有能量低于 22 kHz$$ 的信号效率不高。例如与使用 $$f_s=44 kHz$$ 的系统相比，此采样方案将存储样本的内存增加 $$8$$ 倍。这就是为什么，即使我们已经利用 $Y_{c} (j Ω)$ ，如果我们增加采样频率，副本将达到更高的频率，并且重建滤波器可以从通带到阻带有更平滑的过渡。例如，假设 $y_{c} (t)$ 表示带能量的模拟音乐波形 $0 < \frac{| Ω |}{2 π} < 22 k H z$ .如果我们抽样 $y_{c} (t)$ 具有采样频率 $8$ 比奈奎斯特采样率高几倍， $f_{s, n e w} = 352 k H z$ , 那么重建滤波器的过渡带为 $(Ω_{s} ? Ω_{N}) ? Ω_{N} = 2 π \times 308 k H z$ （见图 2）。但是使用效率不高 $352, 000$ 每秒样本以表示其所有能量低于 $22 k H z$ .例如，此采样方案将增加用于存储样本的内存： $8$ 与使用的系统相比的时间 $f_{s} = 44 k H z$ .这就是为什么，即使我们已经利用 A/D 转换期间的过采样，我们对数字数据应用抽取以减少样本数量。

因此，$$y（n）$$ 通常使用尽可能少的样本数来表示给定的 $$y_c（t）$$。问题是：我们能否在数字域中处理y（n），并通过在现有样本之间进行插值来提高采样率？如果我们能做到这一点，我们就可以提高采样率，从而达到放宽重建滤波器要求的重要目标。 $y (n)$ 通常使用尽可能少的样本来表示给定的样本 $y_{c} (t)$ .问题是：我们能否在数字域中处理y（n），并通过在现有样本之间进行插值来提高采样率？如果我们能做到这一点，我们就可以提高采样率，从而达到放宽重建滤波器要求的重要目标。

插值

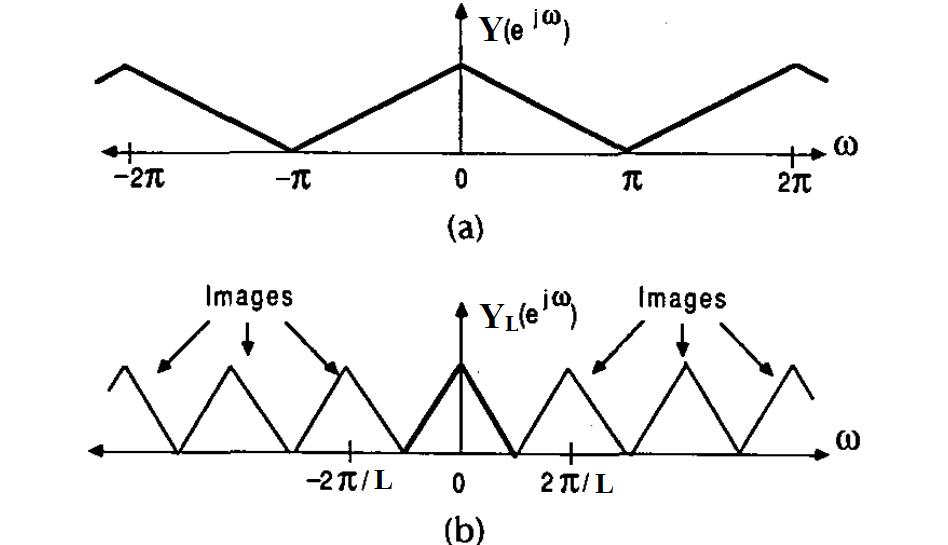
我们希望以数字方式提高 $$y（n）$$ 的采样率，但如何提高呢？假设我们将 $$L-1$$ 零值样本放置在 $$y（n）$$ 的相邻样本之间（参见图 3 表示 $$L=2$$）。 $y (n)$ ，但是如何呢？假设我们放置 $L ? 1$ 相邻样本之间的零值样本 $y (n)$ （参见图 3 $L = 2$ ).

图 3.在离散时间信号的相邻样本之间添加一个零值样本。图片由IEEE提供。

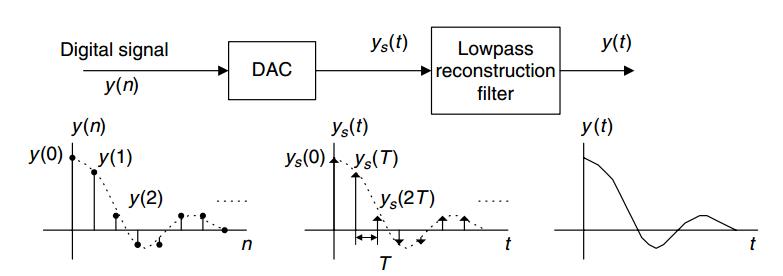
显然，这增加了采样率，但我们添加的样本基本上似乎没有携带任何信息，因为它们与 $$y(n)$$ 的现有样本完全无关。然而，检查所获得序列的傅立叶变换被证明是值得的。让我们将新序列命名为 $$y_l(n)$$，然后当 $$n$$ 是 $$L$ 的倍数时，我们有 $$y_l(n)=y(n\text{/}L)$$ $ 否则为零。我们得到 $$y_l(n)$$ 的傅里叶变换为 $y (n)$ .然而，检查所获得序列的傅里叶变换被证明是值得的。让我们命名新序列 $y_{l} (n)$ ，那么我们有 $y_{l} (n) = y (n / L)$ 什么时候 $n$ 是的倍数 $L$ 否则为零。我们得到傅立叶变换 $y_{l} (n)$ 作为

$Y_{l} (e^{j ω}) = \sum_{n = ? \infty}^{+ \infty} y_{l} (n) e^{? j n ω}$

但是，只有当 $$n=kL$$ 时 $$y_l(n)$$ 才非零，其中 $$k$$ 是整数。考虑到 $$y_l(n)$$ 的非零值与 $$y(n)$$ 相关，我们得到 $y_{l} (n)$ 仅当 $n = k L$ ，在哪里 $k$ 是一个整数。考虑到非零值的事实 $y_{l} (n)$ 与 $y (n)$ ，我们获得

$Y_{l} (e^{j ω}) = \sum_{k = ? \infty}^{+ \infty} y_{l} (k L) e^{? j k L ω} = \sum_{k = ? \infty}^{+ \infty} y (k) e^{? j k L ω} = Y (e^{j L ω})$

上述等式意味着 $$y_l（n）$$ 的频谱与 $$y（n）$$ 的频谱相同，除了需要应用于 $$\omega$$ 轴的缩放。如图 4 所示。 $y_{l} (n)$ 是一样的 $y (n)$ 除了缩放需要应用于 $ω$ 轴。这在图 4 中进行了说明。

图4. 在 y（n）的相邻样本之间添加 L-1 零值样本的效果。图片由国际电气和电子工程师.

检查上面的光谱，我们发现可以从 $$Y_l(e^{j\omega})$$ 的光谱中提取 $$Y(e^{j\omega})$$ 的光谱。为此，我们只需要应用一个尖锐的低通滤波器，其归一化截止频率为 $$\frac{\pi}{L}$$ 到 $$y_l(n)$$。这将忽略 $$\frac{\pi}{L}$$ 以上的所有频率分量，通常称为图像（见图 4）。请注意，此滤波器是数字滤波器，我们可以在数字域中实现尖锐的幅度响应和线性相位响应。 $Y (e^{j ω})$ 从那个 $Y_{l} (e^{j ω})$ .为此，我们只需要应用一个尖锐的低通滤波器，其归一化截止频率为 $\frac{π}{L}$ 到 $y_{l} (n)$ .这将忽略上面的所有频率分量 $\frac{π}{L}$ ，通常称为图像（见图 4）。请注意，此滤波器是数字滤波器，我们可以实现尖锐的幅度响应以及

虽然图 4 表明 $$Y_l(e^{j\omega})$$ 的 $$\omega$$ 轴与 $$Y(e^{j\omega})$$ 的频谱相比是按比例缩放的，如果我们以每秒周期数来考虑频率，则没有频率缩放。我们知道 $$f=\frac{\omega}{2\pi T}$$，其中 $$T$$ 是采样周期，$$\omega$$ 是归一化频率。在图 4(a) 中，采样周期为 $$T=\frac{1}{f_s}$$，与 $$\omega=\pi$$ 相关的点给出 $$f=\frac{f_s} {2}$$。在图 4(b) 中，采样周期为 $$\frac{T}{L}$$ 并且 $$\omega=\frac{\pi}{L}$$ 对应于 $ω$ 的轴线 $Y_{l} (e^{j ω})$ 与频谱相比被缩放 $Y (e^{j ω})$ ，如果我们以每秒周期数来考虑频率，则没有频率缩放。我们知道 $f = \frac{ω}{2 π T}$ ，在哪里 $T$ 是采样周期和 $ω$ 是归一化频率。在图4(a)中，采样周期为 $T = \frac{1}{f_{s}}$ , 以及与 $ω = π$ 给 $f = \frac{f_{s}}{2}$ .在图 4(b) 中，采样周期为 $\frac{T}{L}$ 和 $ω = \frac{π}{L}$ 对应于

$f = \frac{\frac{π}{L}}{2 π \frac{T}{L}} = \frac{f_{s}}{2}$

因此，虽然采样率增加 $$L$$，但如果我们以每秒周期数来考虑频率，则频率轴上没有缩放。 $L$ , 如果我们以每秒周期数来考虑频率，则频率轴上没有缩放比例。

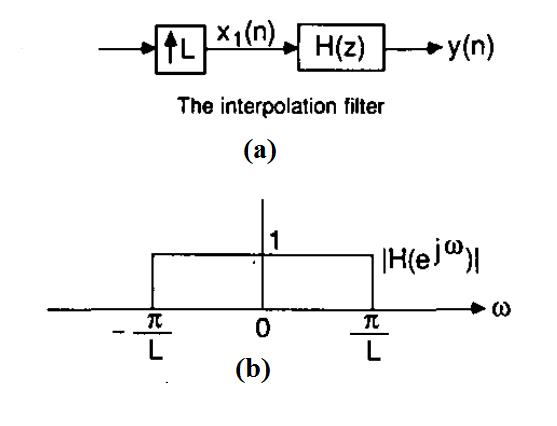
总之，为了提高离散时间序列 $$y(n)$$ 的采样率，我们在相邻样本之间放置 $$L-1$$ 个零值样本，并应用归一化截止频率为$$\frac{\pi}{L}$$ 到得到的序列。这在图 5 中进行了说明。 $y (n)$ ，我们放置 $L ? 1$ 相邻样本之间的零值样本，并应用具有归一化截止频率的低通滤波器 $\frac{π}{L}$ 到得到的序列。这在图 5 中进行了说明。

图 5.上采样后跟一个归一化截止频率为 $$\frac{\pi}{L}$$ 的低通滤波器执行插值。图片由IEEE提供。 $\frac{π}{L}$ 执行插值。图片由

现在，让我们回到设计高效 D/A 级的问题。

插值放宽了重建滤波器的要求

如上所述，增加 $$y(n)$$ 的采样率可以将 $$y_c(t)$$ 的频谱副本移动到更高的频率，从而使模拟滤波器的实现更加可行。图 6 显示了我们如何在 D/A 阶段之前在数字域中应用插值。 $y (n)$ 可以移动频谱的副本 $y_{c} (t)$ 到更高的频率，从而使模拟滤波器的实施更加可行。图 6 显示了我们如何在 D/A 阶段之前在数字域中应用插值。

图 6. D/A 阶段之前的插值。图片由数字信号处理提供。

如图所示，本系统中有两种采样率，$$f_s$$和$$Lf_s$$。插值滤波器的截止频率为 $$\frac{fs}{2}$$，用于去除上面讨论的图像。这样，对模拟滤波器的要求就不那么苛刻了，因为它只需要抑制$$Lf_s$$的倍数的甚高频分量。 $f_{s}$ 和 $L f_{s}$ .插值滤波器的截止频率为 $\frac{f s}{2}$ 并用于删除上面讨论的图像。这样，对模拟滤波器的要求就不那么苛刻了，因为它只需要抑制成倍数的甚高频分量 $L f_{s}$ .

实用 D/A 转换器输出的零阶保持

在图 1 中，我们假设理想 DAC 的输出是脉冲序列；然而，实际上，不可能产生这些窄脉冲。相反，实用的 DAC 通常会保留一个输出值，直到生成下一个值。这称为零阶保持，可以通过在理想 DAC 的输出端放置采样保持来表示（见图 7）。

图 7.实用的 DAC 通常对输出值应用零阶保持。图片由数字信号处理提供。

如图所示，$$y_s(t)$$ 的频谱必须乘以零阶保持块的传递函数。可以证明零阶保持的传递函数为 $y_{s} (t)$ 必须乘以零阶保持块的传递函数。

$H (j Ω) = t_{h} \frac{s i n (Ω \frac{t_{h}}{2})}{Ω \frac{t_{h}}{2}}$

公式 1

其中$$t_h$$表示保持时间，一般等于采样周期，$$T=\frac{1}{f_s}$$。 $t_{h}$ 表示保持时间，一般等于采样周期， $T = \frac{1}{f_{s}}$ .

假设图 7 中的 $$y(n)$$ 对应于一个连续时间信号 $$y_c(t)$$，其所有能量都低于 $$f_N=\frac{f_s}{2}$$，并且我们通过以 $$f_s$$ 的采样率对 $$y_c(t)$$ 进行采样获得了 $$y(n)$$。在这种情况下，零阶保持的响应和 $$y_s(t)$$ 的频谱将如图 8 所示。 $y (n)$ 在图 7 对应于一个连续时间信号 $y_{c} (t)$ 它的所有能量都在下面 $f_{N} = \frac{f_{s}}{2}$ ，并且我们已经获得 $y (n)$ 通过抽样 $y_{c} (t)$ 与采样率 $f_{s}$ .在这种情况下，零阶保持的响应和频谱 $y_{s} (t)$ 将如图 8 所示。

图 8.零阶保持的幅度响应 $$H(j2 \pi f)$$ 和 $$y_s(t)$$ 的频谱。图片由CMOS 集成模数和数模转换器 $H (j 2 π f)$ , 和光谱 $y_{s} (t)$ .图片由提供。

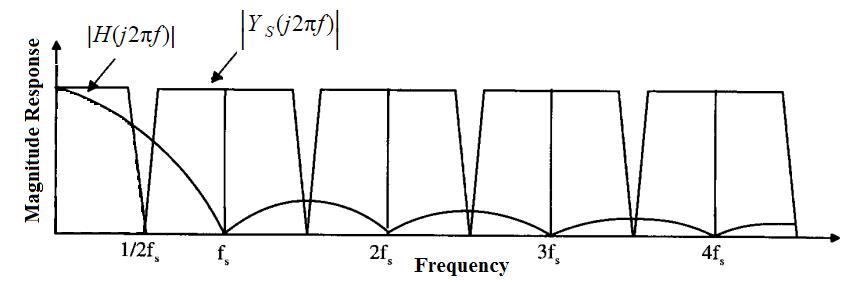
图 8 显示 $$y_c(t)$$ 的频率分量在 $$\frac{f_s}{2}$$ 附近比低频分量衰减得更多。检查 $$H(j\Omega)$$ 在 $$\Omega=0$$ 和 $$\Omega=2 \pi \frac{f_s}{2}$$，我们观察到零阶保持函数展示$$\Omega=2 \pi \f_s}{2}$$ 的衰减比 $$\Omega=0$$ 附近的低频分量多近 $$3.9 dB$$。这是一种众所周知的幅度降低，称为 $$\frac{sin(x)}{x}$$ 失真。 $y_{c} (t)$ 周围的 $\frac{f_{s}}{2}$ 比低频分量衰减得更多。检查 $H (j Ω)$ 在 $Ω = 0$ 和 $Ω = 2 π \frac{f_{s}}{2}$ ，我们观察到零阶保持函数几乎表现出 $3.9 d B$ 更多的衰减 $Ω = 2 π \frac{f_{s}}{2}$ 比附近的低频分量 $Ω = 0$ .这是一个众所周知的振幅减少，称为 $\frac{s i n (x)}{x}$ 失真。

现在，假设我们对 $$y(n)$$ 应用 L 倍插值并将采样率增加到 $$f_{s, new}=Lf_s$$。在这种情况下，我们有 $$t_h=\frac{1}{Lf_s}$$。 $$H(j\Omega)$$ 对于 $$y_c(t)$$ 的高频分量在 $$f_N=\frac{f_s}{2}$$ 附近的衰减是多少？代入等式 1 中的值，我们得到 $y (n)$ 并将采样率提高到 $f_{s, n e w} = L f_{s}$ .在这种情况下，我们有 $t_{h} = \frac{1}{L f_{s}}$ .什么是衰减 $H (j Ω)$ 对于高频分量 $y_{c} (t)$ 大约 $f_{N} = \frac{f_{s}}{2}$ ？代入等式 1 中的值，我们得到

$| H (j 0) | = t_{h}$

$| H (j 2 π \frac{f_{s}}{2}) | = t_{h} \frac{s i n (\frac{π}{2 L})}{\frac{π}{2 L}}$

当我们使用更大的 $$L$$ 时，$$\frac{sin( \frac{\pi}{2L} ) } { \frac{\pi}{2L} }$$ 趋向于 1 并且 $$ 的衰减$H(j\Omega)$$ 减少。 $L$ , $\frac{s i n (\frac{π}{2 L})}{\frac{π}{2 L}}$ 趋向于一个和衰减 $H (j Ω)$ 减少。

总之，插值不仅放宽了重建滤波器的要求，而且使 $$\frac{sin(x)}{x}$$ 失真不那么严重。 $\frac{s i n (x)}{x}$ 失真不太严重。

上一篇：探索用于噪声系数测量的 Y 因子方法

下一篇：电压模式R-2R DAC的工作原理和特性