模糊逻辑不需要奇怪的硬件或新的编程语言,只需要一种不同的方法来设置成员资格。从电梯到锅炉的大量物理系统都可以从模糊逻辑编程中受益。本文探讨了如何对商用 DSP
芯片进行编程来创建基本的模糊逻辑控制器。
您可以使用标准的现成
微处理器来构建模糊逻辑系统。但是,如果您正在设计一个实时、安全关键的系统怎么办?模糊逻辑控制器有时需要更多的处理能力才能实时工作。传统微
处理器足以满足大多数应用(甚至模糊逻辑应用)的需求,但并不总是适合需要极快和可预测响应时间的安全关键应用。当传统处理器不够快时,数字
信号处理器 (DSP) 可能正是您的系统所需要的。
DSP 是一种具有面向数学的功能和指令集的专用微处理器,初仅用于信号处理应用。现在,随着 DSP 软件
开发工具的种类和质量的提高,它们变得越来越流行。DSP 现在与通用微处理器相比具有成本竞争力。如今,任何可以从高速乘法/累加 (MAC) 运算中受益的应用程序都是 DSP 处理器的候选者。
在本文中,我将描述模糊逻辑系统的组件,并举例说明如何使用 DSP 来实现模糊逻辑系统。
模糊逻辑基础
Lotfi Zadeh 被认为是模糊逻辑的创始人,他在 1965 年的一篇论文中提出了布尔集合论的扩展,该集合论是多值的而不是二值的。他的模糊逻辑集合论是经典集合论的推广——一种很好地处理不性的推广。模糊逻辑的强大之处在于,它使您能够在不使用数学的情况下准确地描述过程或行为。
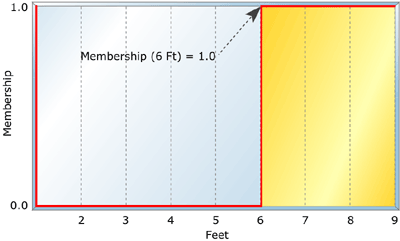
图 1:Tall 的布尔变量】
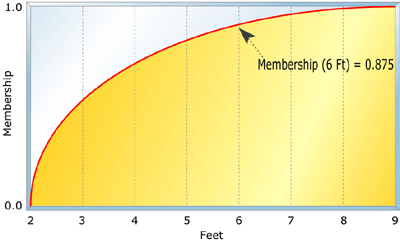
图 2:高的模糊变量
布尔集要么为真,要么为假,而模糊集可以具有部分成员资格。例如,图 1 显示了一个布尔变量。在布尔表中,“Tall”对于 6 英尺或以上为 true,对于小于 6 英尺为 false。但图2中的模糊变量Tall既不是真也不是假;它有不同程度的成员资格。布尔变量通常称为清晰集,模糊变量称为模糊集。
模糊集的行为与清晰的对应行为类似。例如,模糊逻辑使用 AND、OR、NOT 和补码运算符。AND 运算的工作原理是取输入中的较小者。OR-ing 取较大的输入;补码运算符的工作原理是用 1 减去输入的值。
控制器组件
任何基于模糊逻辑的控制器都具有三个组件:模糊器、规则库和去模糊器。每个组件在将清晰(数字)输入转换为模糊值、对该值进行操作,然后将模糊值转换回清晰输出方面都发挥着重要作用。尽管模糊控制器的实现方式不同,但它们都具有这三个基本组成部分。
模糊器 采用清晰的输入值,并通过在必要时缩放输入值并将其转换为多值实体,将其转换为模糊值。缩放将输入的域映射为所有变量使用的某种内部格式。这种多值实体是将输入值与其相应的输入集进行比较并映射该值以反映其成员资格特征的结果。
规则库 获取前一阶段的输入,并将每个相关语句的区域相加。规则库由一系列一个或多个 IF-THEN 语句组成。每个陈述依次由两部分组成:先行词(关键字“then”的左侧)和结果 (“then”的右侧)。一项陈述可能有一个或多个前因和后果。典型的规则声明如下所示:
如果先行词 1 . 。。前因N THEN
后果1 。。。后果N
前因和结果都采用Variable is Condition 的形式,其中Variable 是前因的输入变量或结果的输出变量。结果的条件部分是一个模糊隶属函数,如“冷”、“暖”或“热”。规则库将每个规则与模糊器的数据进行比较。当它遇到正确的先行词时,它会触发语句的结果操作。这种触发动作称为触发。
电梯规则库的示例可能如下所示:
如果门打开且速度为零且距离可忽略不计则电机为零
如果门关闭且速度慢且距离大则电机
如果门关闭且速度为中等且距离适中则电机为平均
如果门关闭且速度快且距离适中则电机为平均
此示例有四个规则,每个规则有四个变量:门、电机、速度和距离(到选定楼层)。每条规则都有三个前因和一个结果。四个变量的隶属度集共有 10 个条件。例如,速度的成员资格集具有零、慢、中和快的值。可变距离具有可忽略、轻微、中等和极大的值。门可以打开或关闭,电机对于相应的会员组有零、值、平均值和值。
对于此示例,我们假设电梯门关闭且其速度为每秒 10 英尺,该速度在慢速和中等隶属度区域中定义(所有隶属度区域彼此重叠)。距离为 42 英尺,对于大区和中等地区都有多重定义。因此,规则库中的两条规则(第二条和第三条规则)被触发,并且结果被平均。
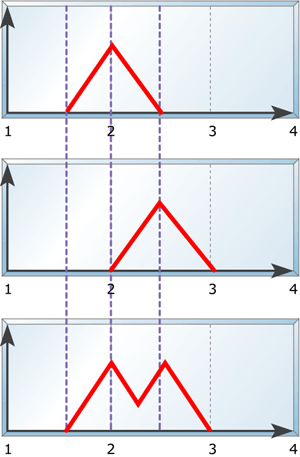
图 3:触发规则库的结果
规则触发 是控制器的规则库组件中的关键元素。当规则触发时,它会导致语句的结果部分变为活动状态。一旦激活,语句的后果部分将与已触发规则的所有其他后果相加。因此,该阶段的输出产生了所有触发结果的组合。从图形上看,这看起来像是解雇后果的所有成员资格集的总和。图 3 显示了电梯示例中规则库的结果。
模糊逻辑控制器的第三个组件是去模糊器。它将前一阶段的输出转换为清晰的输出值。目前有四种流行的去模糊化方法。它们是质心、化、单例和加权平均。每种方法都有自己的优点和缺点,其中质心法是的。我在本文中仅描述质心方法。
质心去模糊化 计算前一阶段的复合模糊集的“质心”。该方法是数值密集型的,需要计算集合的积分。它还要求输出集重叠以避免产生无效输出的情况,并且每个变量的隶属度集由奇数或奇数个区域组成。


