使用等效噪声温度表征 RF 噪声分量

时间：2023-05-30

之前，我们讨论了噪声系数是射频工作中常用的噪声指标。表征 RF 组件和系统噪声性能的另一种方法是等效噪声温度，这将是本文的主要关注点。

通常，噪声系数和等效噪声温度都提供相同的信息；但是，您可能不太熟悉噪声温度的概念。噪声温度主要用于非地面应用，例如射电天文学和面向空间的无线电链路，它们处理非常小的噪声水平。尽管它的应用范围不大，但熟悉噪声温度概念可以让我们更清楚地了解噪声系数测量仪器的实际工作原理。事实上，自动噪声系数分析仪可能会根据噪声温度执行许多内部计算。

单端口设备的噪声温度：天线或噪声源

我们可以使用噪声温度的概念来指定单端口设备（例如天线或噪声源）产生的噪声。为了更好地理解这一点，考虑一个输出阻抗为 R 的任意白噪声源连接到一个匹配的负载电阻R L，如下面的图 1(a) 所示。

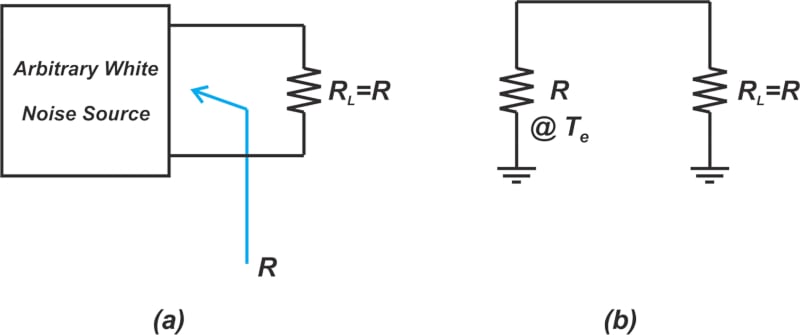
任意白噪声源的示例图，其输出阻抗连接到匹配的负载电阻器 (a) 和温度为 Te 的单个电阻器，产生与原始噪声源相同的噪声量 (b)。

图 1. 任意白噪声源的示例图，其输出阻抗连接到匹配的负载电阻器 (a) 和温度为 T e的单个电阻器，产生与原始噪声源相同的噪声量 (b)。

假设噪声源提供的噪声功率为 N o 至 R L = R（即，噪声源的可用噪声功率为 N o）。我们知道电阻器的可用噪声功率是 kTB。将 kTB 等同于 N o ，我们可以找到电阻器呈现可用噪声功率 N o时的温度。

Te=NokB $T_{e} = \frac{N_{o}}{k B}$

这一观察为我们提供了图 1(b) 中所示的噪声模型，其中温度为 T e的单个电阻器 R 用于产生与原始噪声源相同数量的噪声，其中 T e 是等效噪声噪声源的温度。请注意，噪声温度并不表示电阻器的物理温度，因为您会用温度计测量它。噪声温度只是一个概念，它使我们能够对组件产生的实际噪声水平进行建模。还值得一提的是，根据定义，噪声系数概念不能应用于单端口设备。

二端口设备的噪声温度：噪声放大器

噪声温度的概念也可以用来描述双端口网络的噪声性能。例如，考虑一个具有增益 G 和带宽 B 的噪声放大器，连接到一个匹配的源电阻器，如图 2(a) 所示。

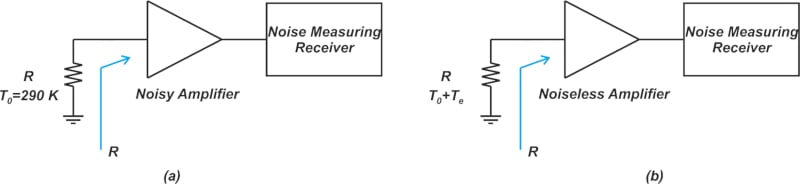
噪声测量系统中有噪声 (a) 和无噪声 (b) 放大器的示例图。

图 2. 噪声测量系统中有噪声 (a) 和无噪声 (b) 放大器的示例图。

接下来，可以使用公式 1 描述放大器输出端的可用噪声。

$N_{o} = N_{o (添加)} + k T_{0} B G$

等式 1。

在哪里：

No o(added) 是由放大器的内部噪声源产生的噪声部分
kT 0 BG 是来自源电阻器 (kT 0 B) 的可用噪声乘以放大器的可用功率增益 G

与单端口示例类似，我们希望通过为源电阻器找到一个新温度来对来自放大器的噪声进行建模。为此，我们首先找到放大器的输入参考噪声：

$N_{i (添加)} = \frac{N_{o (添加)}}{G}$

将上述值与 kT e B 相等可以得到等效温度，其中电阻器的可用噪声功率等于等式 2 中放大器的输入参考噪声。

$T_{e} = \frac{N_{o (添加)}}{k B G}$

等式 2。

由此，我们可以假设放大器是无噪声的，而是将Rs的初始温度增加 Te 以解决放大器的噪声问题。如图 2(b) 所示。

现在，让我们通过计算总输出噪声来验证我们的模型。参考图 2(b)，我们有：

$\begin{array}{rcl} N_{o} & = & k T B G = k (T_{0} + T_{e}) B G \\ = & k (T_{0} + \frac{N_{o (a d d e d)}}{k B G}) B G \\ = & k T_{0} B G + N_{o (a d d e d)} \end{array}$

这与公式 1 一致（不足为奇！）。有了放大器的噪声温度 T e，我们就能够找到整个系统的噪声温度，包括源阻抗 R s和由 T 0 + T e 给出的放大器。此外，通过将公式 2 与下面的噪声因子定义相结合，我们可以获得一个有用的公式，该公式根据等效噪声温度来表示噪声系数，如公式 3 所示。

$\begin{array}{rcl} F & = & 1 + \frac{N_{o (a d d e d)}}{N_{o (s o u r c e)}} \\ = & 1 + \frac{k T_{e} B G}{k T_{0} B G} \\ = & 1 + \frac{T_{e}}{T_{0}} \end{array}$

等式 3。

级联系统的噪声温度

由 N 个二端口设备组成的级联系统如下图 3 所示。

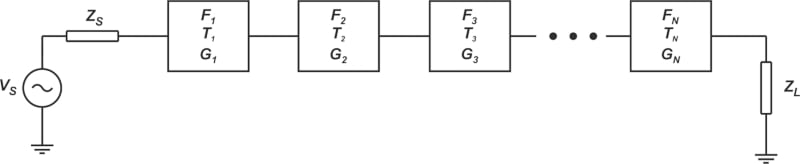
由 N 个二端口设备组成的级联系统图。

图 3. 由 N 个二端口设备构成的级联系统图。

在哪里：

F i 是噪声因子
T i 是等效噪声温度
G i 是第i级的可用功率增益

考虑到这一点，我们知道级联系统的噪声系数是：

$F = F_{1} + \frac{F_{2} ? 1}{G_{1}} + \frac{F_{3} ? 1}{G_{1} G_{2}} + ? + \frac{F_{N} ? 1}{G_{1} G_{2} \dots G_{N ? 1}}$

应用等式 3，我们可以用等效噪声温度替换每个 F i项，并找到级联系统的噪声温度：

$T_{c a s} = T_{1} + \frac{T_{2}}{G_{1}} + \frac{T_{3}}{G_{1} G_{2}} + ? + \frac{T_{N}}{G_{1} G_{2} \dots G_{N ? 1}}$

如果 T s 表示源阻抗的噪声温度，则整个系统（包括 R s 和级联）的噪声温度为 T s + T cas。

现在，让我们看几个例子来阐明上述概念。

示例 1：指定噪声系数以满足系统要求

假设对于 T s = 60 K 的源温度，整个系统的噪声温度为 380 K。找出级联的噪声系数。

级联本身的噪声温度很容易找到 T cas = 380 - T s = 320 K。接下来，我们应用公式 3 来计算所需的级联噪声系数：

$\begin{array}{rcl} F & = & 1 + \frac{T_{e}}{T_{0}} \\ = & 1 + \frac{320}{290} = 2.1 = 3.22 d B \end{array}$

示例 2：查找级联系统输出的噪声功率

假设源噪声温度为 Ts = 150 K。另外，假设级联噪声因子、增益和带宽分别为 F cas = 1.8、G = 6 dB 和 B = 10 MHz。找出级联输出端的可用噪声功率。

我们首先使用公式 3 计算级联的噪声温度：

$T_{c a s} = (F_{c a s} ? 1) T_{0} = (1.8 ? 1) \times 290 = 232 K$

因此，整个系统的噪声温度为T sys = T s + T cas = 150 + 232 = 382 K。，我们有：

$\begin{array}{rcl} N_{o} & = & k (T_{s} + T_{c a s}) B G \\ = & 1.38 \times 10^{? 23} \times 382 \times 10 \times 10^{6} \times 10^{0.6} \\ = & 2.099 \times 10^{? 13} W = ? 96.8 d B m \end{array}$

重温“噪声线”——噪声系数与噪声温度

在之前的文章中，我们查看了总输出噪声与源电阻温度 T 的关系图（图 4）。

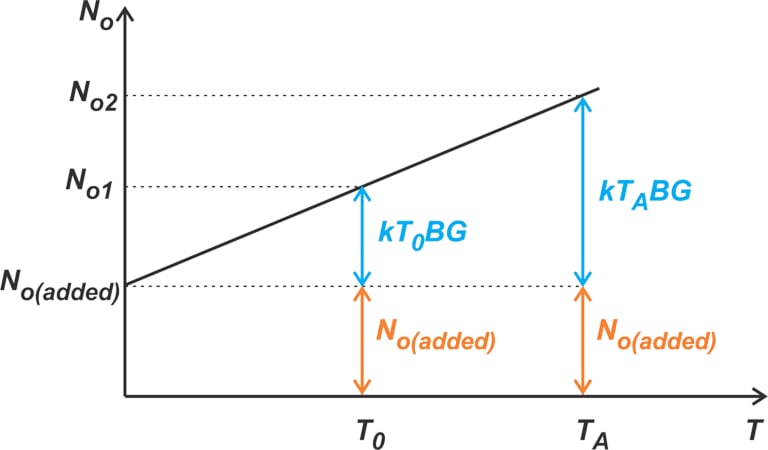
显示总输出噪声与源电阻温度的关系图。

图 4. 显示总输出噪声与源电阻温度的关系图。

这条曲线使我们能够更好地理解噪声系数和噪声温度之间的一个重要区别。噪声系数度量对应于标准温度 T 0。它实际上指定了 R S 在 T 0时（即 kT 0 BG）贡献的输出噪声与被测设备的输出噪声 No (added)之比。从图中可以看出，这个比值随着T的变化而变化，这就是为什么噪声系数是在标准温度下给出的。然而，从公式 2 可以看出，噪声温度直接指定了被测设备添加的噪声 No (added)，它不随 T 变化。此功能允许我们简单地将组件的噪声温度添加到源电阻的任意噪声温度；并使用系统的整体噪声温度来计算输出噪声功率。

另一方面，当源温度 T s与标准温度 T 0 不同时，应用噪声系数概念可能有点棘手。如果 T s ≠ T 0，我们不能直接使用噪声系数定义来计算总输出噪声。在这种情况下，我们应该首先使用噪声系数方程找到 No (added) ，然后使用该信息找到输出噪声。

噪声温度：低噪声系统中的高分辨率指标

表 1 给出了一些示例噪声系数值的噪声温度。

表 1. 噪声系数值的示例噪声温度。数据由Thomas H. Lee提供

噪声系数（分贝）	F	T N (K)
0.5	1.122	35.4
0.6	1.148	43.0
0.7	1.175	50.7
0.8	1.202	58.7
0.9	1.230	66.8
1.0	1.259	75.1
1.1	1.288	83.6
1.2	1.318	92.3
1.5	1.413	120
2.0	1.585	170
2.5	1.778	226
3.0	1.995	289
3.5	2.239	359

请注意，对于噪声极低的系统，噪声温度是对噪声性能的更高分辨率描述。例如，当噪声系数从 0.5 dB 变化到 1 dB 时，噪声温度在相对较大的范围内变化，从 35.4 K 到 75.1 K。噪声系数在这个范围内也有很小的变化，从 1.122 到 1.259。作为更高分辨率的表示，噪声温度通常用于表征处理极低噪声水平的卫星通信系统。

天线噪声温度

作为本文的一节，让我们简要了解一些可能影响天线噪声温度的因素。用作接收元件的天线的电气模型如下所示（图 5）。

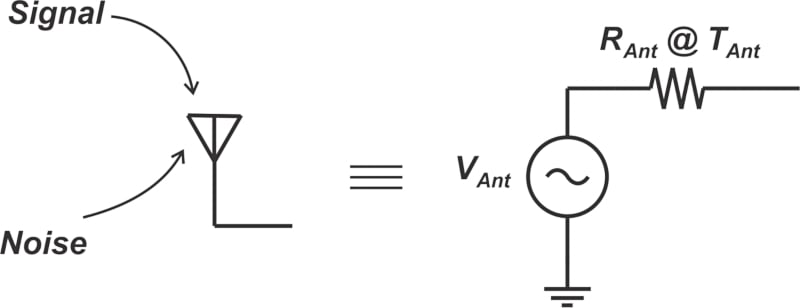
用作接收元件的天线示意图。

图 5. 用作接收元件的天线示意图。

电压源 V Ant代表天线收集信号的能力。R Ant 实际上模拟了天线的匹配特性，将自由空间的特性阻抗与我们电路的特性阻抗相匹配。天线还会拾取撞击其上的信号和噪声分量。

为了对收集到的噪声建模，我们假设 R Ant 处于 T Ant的噪声温度。天线拾取的噪声以及由此产生的 T Ant取决于几个不同的因素，例如天线的位置、仰角和感兴趣的频率。例如，如果天线朝向产生电磁干扰 (EMI) 的电子设备，我们预计会收集到更多的噪声功率。但是，将天线重新放置在远离噪声源的位置可以降低噪声水平。

地平线外的天线仰角也是一个重要参数。在地对地无线电链路中，天线指向地平线。因此，它从地面吸收热辐射，导致典型噪声温度约为 290 K，这是噪声系数定义中使用的标准温度。

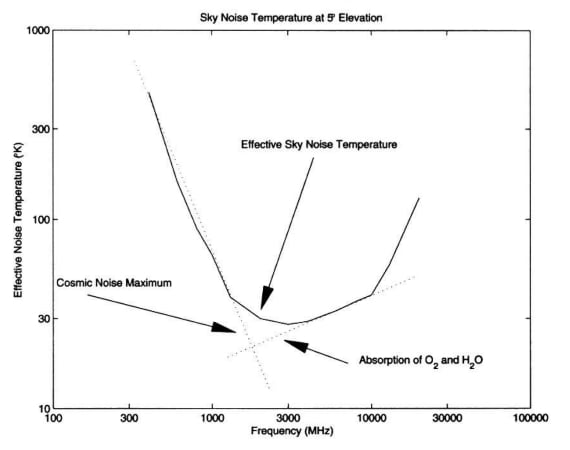
另一方面，在卫星通信中，天线指向天空，等效噪声温度通常要低得多，通常约为 50 K。这就是为什么卫星通信系统要处理极低的噪声水平，并且通常使用噪声温度指标。天线噪声温度也随频率变化。图 6 显示了仰角为 5° 的天线的噪声温度与频率的关系。

显示仰角为 5° 的天线的噪声温度与频率的关系图。

图 6. 显示仰角为 5° 的天线的噪声温度与频率的关系图。图片由Kevin McClaning提供

噪声温度概念总结

噪声系数和噪声温度是噪声性能的可互换表征。噪声温度概念主要用于非地面应用，例如处理非常小噪声水平的射电天文学和面向空间的无线电链路。此外，熟悉噪声温度概念可以让我们更清楚地了解噪声系数测量仪器的实际工作原理。在下一篇文章中，我们将讨论一种常用的噪声系数测量方法，即广泛使用噪声温度概念的 Y 因子法。

上一篇：耗尽层与过渡电容

下一篇：使用 LTspice 和负电压发生器探索负电压