Scilab 中的数字信号处理：如何解码 FSK 信号

了解从解调频移键控基带信号中提取原始数字数据的 DSP 技术。

相关信息

• 数字调制：幅度和频率（来自AAC的RF教材第4章）
• 如何解调数字相位调制

以前关于基于 Scilab 的数字信号处理的文章

• Scilab 正弦信号处理简介
• 如何使用 Scilab 执行频域分析
• 如何使用 Scilab 分析调幅射频信号
• 如何使用 Scilab 分析调频射频信号
• 如何对数字化音频信号进行调频
• Scilab 中的数字信号处理：如何使用音频处理滤波器去除录音中的噪声
• Scilab 中的音频处理：如何实现频谱减法

用于在正弦波形中对二进制数据进行编码的方法之一称为频移键控 (FSK)。这是一个简单的概念：一个频率代表零，不同的频率代表一。例如：

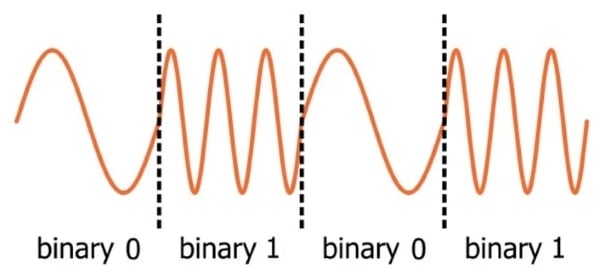
低频 FSK 信号（例如，几十千赫兹）可以转换为更高频率，然后传输。这是创建实现数字数据无线传输的 RF 系统的一种有效且相当直接的方法——假设我们有一个接收器可以将所有这些正弦波形转换回 1 和 0。

从传输的 FSK 信号中提取数字数据的过程可分为两个一般任务：首先，将高频接收信号转换为低频基带信号。我将此称为“解调”。其次，必须将基带波形转换为 1 和 0。我不认为将这第二步称为“解调”是不正确的，但为了避免混淆，当我谈论将低频模拟波形转换为数字位时，我将始终使用术语“解码”。

软件解码

对于数据速率适中的系统，将 FSK 基带信号数字化并在软件中进行解码是完全可行的。（您可以查看我们对软件定义无线电的介绍， 了解有关在软件中实现重要信号处理任务的射频系统的更多信息。）在我看来，这是一种极好的方法，因为它允许接收器受益于数字信号处理，它还提供了一种在测试过程中记录和分析接收信号的便捷方式。

在本文中，我们将使用 Scilab 对 FSK 信号进行解码，但所涉及的计算并不复杂，并且可以很容易地在数字信号处理器中以 C 代码的形式实现。

要事：数学

我们解码 FSK 的技术基于正弦信号的乘积。考虑以下三角恒等式：

sin(x)?sin(y)=12(cos(xy)?cos(x+y))<span style="color:#000000;">sin</span><span style="color:#000000;">?</span><span style="color:#000000;">(</span><span style="color:#000000;">x</span><span style="color:#000000;">)</span><span style="color:#000000;">?</span><span style="color:#000000;">sin</span><span style="color:#000000;">?</span><span style="color:#000000;">(</span><span style="color:#000000;">y</span><span style="color:#000000;">)</span><span style="color:#000000;">=</span><span style="color:#000000;">1</span><span style="color:#000000;">2</span><span style="color:#000000;">(</span><span style="color:#000000;">cos</span><span style="color:#000000;">?</span><span style="color:#000000;">(</span><span style="color:#000000;">x</span><span style="color:#000000;">y</span><span style="color:#000000;">)</span><span style="color:#000000;">?</span><span style="color:#000000;">cos</span><span style="color:#000000;">?</span><span style="color:#000000;">(</span><span style="color:#000000;">x</span><span style="color:#000000;">+</span><span style="color:#000000;">y</span><span style="color:#000000;">)</span><span style="color:#000000;">)</span>

$$\cos \left(x\right)?\cos \left(y\right)=\frac{1}{2}\left(\cos \right(xy)+\cos (x+y\left)\right)$$

让我们使用 ω 1 t 和 ω 2 t 代替 x 和 y，使其更符合工程界。

$$\sin \left({\omega }_{1}t\right)?\sin \left({\omega }_{2}t\right)=\frac{1}{2}\left(\cos \right(({\omega }_1?{\omega }_2)t)?\cos (({\omega }_1+{\omega }_2)t\left)\right)$$

$$\cos \left({\omega }_{1}t\right)?\cos \left({\omega }_{2}t\right)=\frac{1}{2}\left(\cos \right(({\omega }_1?{\omega }_2)t)+\cos (({\omega }_1+{\omega }_2)t\left)\right)$$

（请注意，我们忽略了相位差的影响；在本文中，我们假设所有信号都具有相同的相位。）我们可以将两个正弦波或两个余弦波相乘，结果由两个余弦波组成，频率为等于两个原始频率的和与差。这里的关键观察是，如果两个输入波具有非常相似的频率，则 cos((ω 1 –ω 2 )t) 波形将具有非常低的频率。在理想化的数学领域，我们可以输入两个相同频率和 cos((ω 1 –ω 2)t) 变为 cos(0t) = cos(0) = 1。因此，如果我们将两个相同频率的正弦波或两个余弦波相乘，得到的波形将具有相对较大的直流偏移。

在解码 FSK 的上下文中，我们可以这样说：即使频率相似而不是相同，仍然会有很大的直流偏移，因为 cos((ω 1 –ω 2 )t)波形将从1开始并且相对于一位周期下降得非常缓慢. 位周期是编码一个数字位所需的时间量；在上图中，位周期对应二进制 0 频率的一个周期（或二进制 1 频率的三个周期）。一个比特周期中包含的模拟波形部分称为符号。在本文中，我们使用二进制（即双频）FSK，因此一个符号对应一个数字位。可以使用两个以上的频率，这样一个符号可以传输多个比特。

逐步解码 FSK

我们现在有了制定 FSK 解码程序所需的信息：

1. 将接收到的基带信号数字化。
2. 识别位周期的开始。这可以在训练序列的帮助下完成；有关更多信息，请单击此处并向下滚动到“数据包剖析”部分中的“序言”标题。对于本文，我们假设数据被编码为正弦波（如上图所示）而不是余弦波。
3. 将每个符号乘以二进制 0 频率的正弦波和二进制 1 频率的正弦波。
4. 计算每个符号的直流偏移。
5. 选择一个阈值并根据符号的直流偏移是高于还是低于阈值来决定二进制 0 和二进制 1。

Scilab 实施

我们将从以二进制 0 频率 (10 kHz) 和二进制 1 频率 (30 kHz) 生成单符号正弦波形开始。

零频 = 10e3；
OneFrequency = 30e3;
采样频率 = 300e3；
Samples_per_Symbol = 采样频率/零频率；
n = 0:(Samples_per_Symbol-1);
Symbol_Zero = sin(2*%pi*n / (SamplingFrequency/ZeroFrequency));
Symbol_One = sin(2*%pi*n / (SamplingFrequency/OneFrequency));
绘图（n，Symbol_Zero）
绘图（n，Symbol_One）

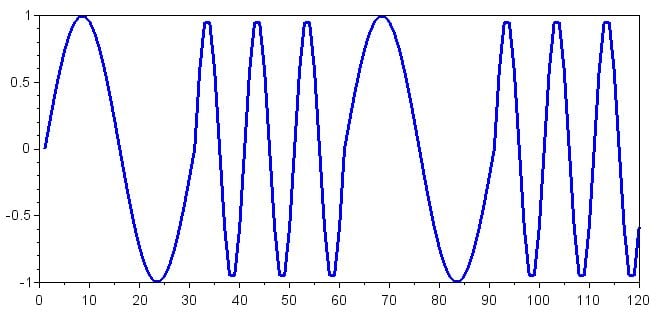
现在让我们创建接收到的基带信号。我们可以通过连接Symbol_Zero和Symbol_One数组来做到这一点；我们将使用序列 0101：

ReceivedSignal = [Symbol_Zero Symbol_One Symbol_Zero Symbol_One];
情节（接收信号）

接下来，我们将接收信号中的每个符号乘以二进制 0 符号的波形和二进制 1 符号的波形。我们根据接收信号中的符号数连接Symbol_Zero和Symbol_One数组，然后使用逐元素乘法来完成此步骤；有关 Scilab（或 MATLAB）中逐元素乘法的更多信息，请参阅本文。

Decoding_Zero = ReceivedSignal .* [Symbol_Zero Symbol_Zero Symbol_Zero Symbol_Zero];
Decoding_One = ReceivedSignal .* [Symbol_One Symbol_One Symbol_One Symbol_One];
情节（解码_零）

情节（解码_一） 

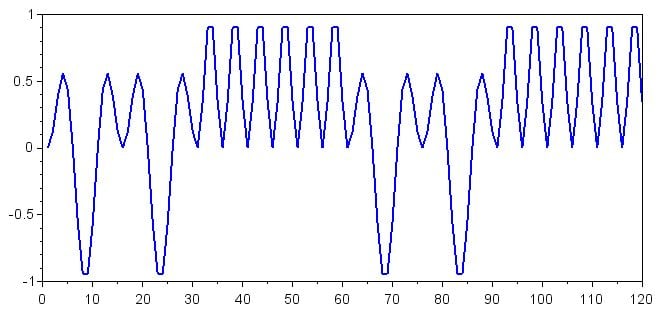
不要被这些相当复杂的波形分心；我们感兴趣的只是直流偏移，用数学术语来说就是平均值。如果我们要显示每个交易品种对应的DC偏移量，我们首先需要生成一些新的数组：

对于 k=1:(length(Decoding_Zero)/Samples_per_Symbol)
  > SymbolOffsets_Zero(((k-1)*Samples_per_Symbol)+1:k*(Samples_per_Symbol)) = mean(Decoding_Zero(((k-1)*Samples_per_Symbol)+1:k*(Samples_per_Symbol)));
  > 结束  
对于 k=1:(length(Decoding_One)/Samples_per_Symbol)
  > SymbolOffsets_One(((k-1)*Samples_per_Symbol)+1:k*(Samples_per_Symbol)) = mean(解码_One(((k-1)*Samples_per_Symbol)+1:k*(Samples_per_Symbol)));
  > 结束

您可能需要稍微思考一下这些命令才能准确理解我在做什么，但基本思想如下：for 循环用于通过 Decoding_Zero 和 Decoding_One 数组处理一个符号。在SymbolOffsets_Zero和SymbolOffsets_One数组中，一个符号对应的所有数据点都填充了Decoding_Zero和Decoding_One数组中相关符号的均值。每个符号有 30 个样本，因此个命令对数组值 1 到 30 进行操作，下一个命令对数组值 31 到 60 进行操作，依此类推。以下是结果：

情节（SymbolOffsets_Zero）

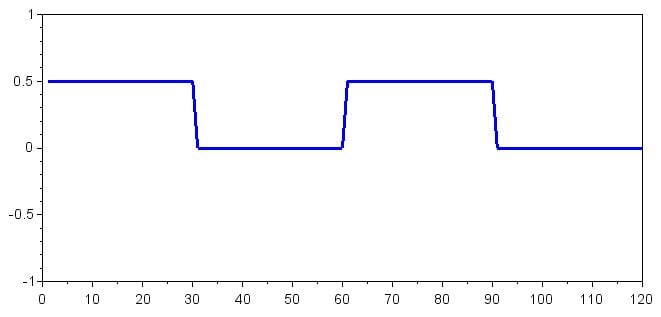
情节（SymbolOffsets_One）

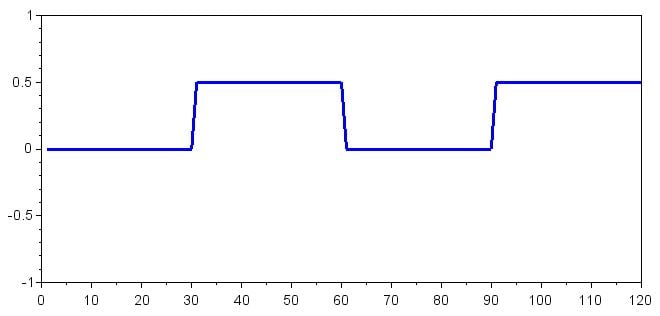
SymbolOffsets_Zero数组显示接收到的基带符号与二进制 0 频率相乘产生的 DC 偏移，SymbolOffsets_One数组显示接收到的基带符号与二进制 1 频率相乘产生的 DC 偏移。我们知道，将两个相似的频率相乘会产生比较大的直流偏移。因此， SymbolOffsets_Zero数组中的值 0.5表示接收到的符号是二进制 0，而SymbolOffsets_One数组中的值 0.5表示接收到的符号是二进制 1。

结论

本文介绍了一种解码 FSK 的数学方法。该过程是在 Scilab 中实现的，但是将 Scilab 命令转换为编程语言（例如 C）并不困难。我们将在下一篇文章中继续使用 FSK 解码。