基于CPU-GPU 异构机群的FDTD 并行算法加速研究（一）

时间：2013-05-14

　　摘要：时域有限差分法（FDTD）求解电磁学中麦克斯韦方程组是科学与工程计算中一个非常重要的算法。通过对FDTD 求解麦克斯韦旋度方程的直接时间域的分析，给出其基于多个GPU 组成异构机群系统上的并行加速算法，用OpenCL、CUDA 和MPI 编程模型实现了并行程序。在目前的主流NVIDIA 和ATI 的GPU 平台上，加速的并行FDTD 程序相对CPU 串行程序和8 个CPU 核的MPI 并行程序，分别获得了超过8 倍和1.5 倍的加速，并在多个GPU 卡上获得了接近线性加速的扩展性能。

　　引言

　　Maxwell 方程组用数学模型揭示了自然界一切宏观电磁现象所遵循的普遍规律，一百多年来，人们依据这组方程将电磁波的研究渗透到各个领域，应用十分广泛，例如微波、天线、电磁成像、电磁防护、无线电传播、导航、雷达技术、地下电磁探测、电磁兼容等等。研究电磁场问题归根结底便是在特定的边界条件下解出Maxwell 方程组的解或近似解。随着计算机技术的迅速发展，已经出现解决Maxwell 方程组的多种有效的数值计算方法，而近40 年发展为迅速的电磁场数值计算方法是时域有限差分（FDTD）方法。FDTD方法是1966 年由K. S. Yee 首次提出，经过几十年的发展，已经应用于辐射天线的分析、微波器件和导行波结构的研究、散射和雷达截面计算、电磁兼容分析、微带线与PBG 结构仿真等多个电磁领域中。而在电磁工程中，存在着一些消耗计算资源巨大的问题，例如大型天线阵列的分析、复杂结构电磁特性仿真等等，诸如这些大规模复杂电磁工程问题，需要的计算量都异常庞大，包含了海量的浮点计算，即使在巨型高性能计算系统中都要运行几个月或者更多的时间。即使是具有单元数量级约为109 的小空间模型，对于一个毫秒级持续时间波形的仿真，传统的高性能计算系统的1000 个处理器也要计算至少一个月的时间。基于传统CPU 编写的现阶段的FDTD 程序对于解决该类问题是非常困难的，需要进一步研究提高这些计算仿真速度的方法。

　　GPU（Graphic Processing Unit）是个人计算机中的重要部件，其主要功能是加速图形处理任务的吞吐率。自从2000年以来，GPU 的浮点运算能力以每12 个月翻一番的速度成指数式增长。到2008 年底，主流GPU 的浮点峰值和显存带宽就已经大大超过了同时代的X86 CPU,相应的，单位功耗可提供的浮点峰值也高出CPU 接近一个数量级。近年来，GPU 在双浮点计算部件、访存层次等方面不断完善，性能、功耗、成本方面的综合优势越来越明显，在高性能计算领域的应用前景越来越广，是实现Peta/Exascale计算技术的重要途径。目前已有大量的科学工程因GPGPU 而获益，相关的研究工作表明利用GPU 的计算能力对求解FDTD 能够获得一定的加速效果。本文根据FDTD 算法和GPGPU 体系结构的特点，提出了一种基于CPU-GPU 异构机群的FDTD 并行计算方法，研究了内存访问和数据通信优化策略，在主流GPGPU 平台上获得了较好的计算加速效果，并且能够支持多个GPGPU 卡的近似线性扩展。

　　1 FDTD 算法概述

　　FDTD 算法的基本思想是：使用差分网格，将连续的电磁场问题变为离散系统问题，用各离散点上的数值解来逼近连续场域内的真实解。计算域空间节点采用Yee 元胞（图1），每个磁场分量由四个电场分量环绕，同样每一个电场分量由四个磁场分量环绕，采用蛙跳格式，电场和磁场在时间顺序上采用交错抽样，这样使得麦克斯韦旋度方程离散后构成显式差分方程，利用前一时刻已知的电场和磁场求出当前时刻的电磁场，在时间上迭代求解。FDTD采用吸收边界条件的方法，把整个计算域划分成包括散射体的总场区以及只有反射波的散射场区，使得计算可以在有限的空间范围内进行。因此，只要给定的相应电磁问题的初始值，通过FDTD 就可以迭代求出此后各个时刻空间电磁场的分布，并在时间轴上逐步推进地求解电磁场。

　　利用中心差分法，可以将 MaxWell 标量方程中更新某个时刻的E 沿Y 轴方向场值写成下面的显示递推方程：

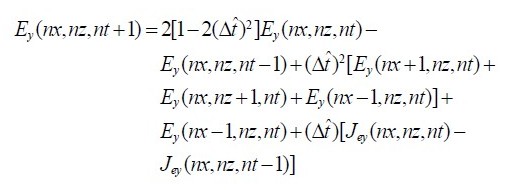
　　另外 5 个递推方程也可以类似推导出来，每个网格点上的场分量的新值依赖于该点在前一时间步长时刻的值及该点周围的临近点上另一场量在早半个时间步长时的值。

　　这样，当某一时刻所有场域内的电磁场计算完后，使用迭代过程就可以计算出随时间变化的网格内电磁场分布情况。FDTD 算法流程如图2 所示。

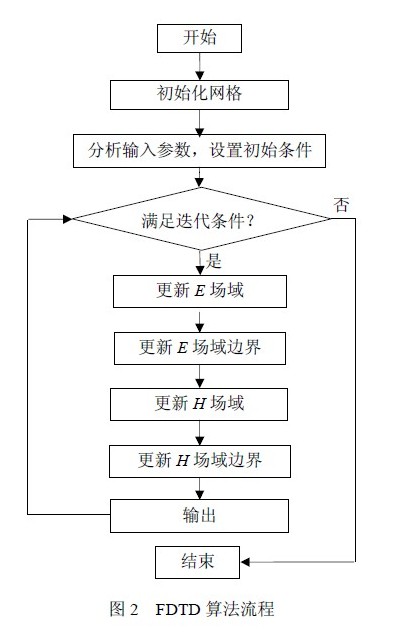
　　为了确定 FDTD 程序中需要加速的函数，我们使用SMALL、MEDIUM 和LARGE 三个数据集对CPU 代码进行了测试，数据集的大小根据网格规模来区分（表1）。在三个数据集下，CPU 算法中的主要函数所占CPU 运行时间比例如表2 所示。在FDTD 的CPU 算法中，大部分时间消耗在电场向量E 和磁场向量H 修正计算的多重循环上。算法执行的复杂度和空间需求估算如下：

　　时间复杂度∝ 6×时间步数×网格数×操作数

　　空间复杂度∝ 6×网格数×常数

　　其中，因数 6 代表在3D 模型中需要修正的分量的个数，常数表示一个浮点数所占的字节。在串行情况下，由于只能算出一个点的场值分量，如果要更新整个网格的场值，就需要一个三重循环进行计算。