基于EKF的异步电机直接转矩控制系统设计与实现

　　随着生产技术的不断发展，直流拖动的薄弱环节逐步显现出来。由于换向器的存在，使直流电动机的维护工作量加大，单机容量、转速以及使用环境都受到限制。人们转向结构简单、运行可靠、便于维护、价格低廉的异步电动机，但异步电动机的调速性能难以满足生产要求。于是，从20世纪30年代开始，人们就致力于交流调速技术的研究，然而进展缓慢。在相当长时期内，在变速传动领域，直流调速一直以其优良的性能于交流调速。60年代以后，特别是70年代以来，电力电子技术和控制技术的飞速发展，使得交流调速性能可以与直流调速相媲美、相竞争。目前，交流调速逐步代替直流调速的时代已经到来。

　　异步电机的状态方程是一组非线性方程，根据系统辨识理论，对非线性系统状态估计的方法是扩展卡尔曼滤波。本文以定子电流和转子磁链为状态变量，将角速度作为估算的参数，利用扩展卡尔曼滤波（EKF）方法估算异步电机的角速度和转子磁链，由此建立异步电机无速度直接转矩控制系统。普通异步电机的定子绕组接交流电网，转子绕组不需与其他电源连接。因此，它具有结构简单，制造、使用和维护方便，运行可靠以及质量较小，成本较低等优点。异步电机有较高的运行效率和较好的工作特性，从空载到满载范围内接近恒速运行，能满足大多数工农业生产机械的传动要求。异步电机还便于派生成各种防护型式，以适应不同环境条件的需要。异步电机运行时，必须从电网吸取无功励磁功率，使电网的功率因数变坏。因此，对驱动球磨机、压缩机等大功率、低转速的机械设备，常采用同步电机。由于异步电机的转速与其旋转磁场转速有一定的转差关系，其调速性能较差（交流换向器电动机除外）。

　　1 扩展卡尔曼滤波器

　　卡尔曼滤波是60年代发展起来的一种现代滤波方法，它的一个重要作用在于系统的状态估计。目前，卡尔曼滤波已经有很多不同的实现。卡尔曼初提出的形式现在一般称为简单卡尔曼滤波器。除此以外，还有施密特扩展滤波器，信息滤波器以及很多Bierman, Thornton 开发的平方根滤波器的变种。常见的卡尔曼滤波器是锁相环，它在收音机，计算机和几乎任何视频或通讯设备中广泛存在。卡尔曼滤波算法是一种应用于线性系统中的迭代估计算法，为了能够在非线性的感应电机模型中应用卡尔曼滤波算法，首先需要将非线性系统线性化。

　　一般非线性系统模型为：

　　式中，W（t）和V（t）分别称为系统噪声矩阵和测量噪声矩阵。测量噪声矩阵由测量的不准确性造成，一般W（t）和V（t）都被假设为零均值的高斯白噪声，其方差矩阵分别为Q和R。

　　对上式的离散随机非线性系统，可以写为

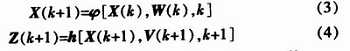
　　式中，ψ[]为n维向量非线性函数；h[]为m维向量非线性函数。

　　将离散随机非线性系统状态方程式中的非线性向量函数ψ[]围绕滤波值展开成泰勒级数，并略去二次以上项，得：

　　这样，非线性系统的状态估计问题就转化为线性系统的状态估计问题了，按照卡尔曼滤波的推演方法，得到EKF算法步骤如下：

　　EKF算法在电机状态估计中的应用如图1所示。

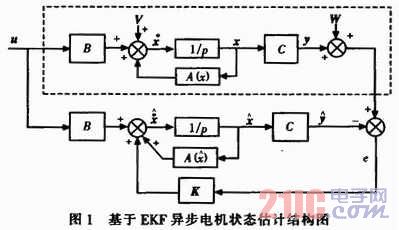
　　图1上半部分的虚框内表示的是电动机实际状态，下半部分是EKF状态估计框图，符号“＾”表示状态矢量估计，K为EKF增益矩阵。

　　2 利用EKF进行转子转速估计

　　虽然应用于非线性状态估计系统中已经得到了学术界认可并为人广泛使用，然而该种方法也带来了两个缺点，其一是当强非线性时EKF违背局部线性假设，Taylor展开式中被忽略的高阶项带来大的误差时，EKF算法可能会使滤波发散；另外，由于EKF在线性化处理时需要用雅克比（Jacobian）矩阵，其繁琐的计算过程导致该方法实现相对困难。所以，在满足线性系统、高斯白噪声、所有随机变量服从高斯（Gaussian）分布这3个假设条件时，EKF是方差准则下的次优滤波器，其性能依赖于局部非线性度。

　　异步电机在两相静止α、β坐标下的数学模型：

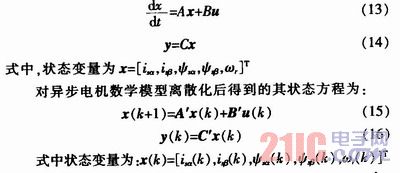
　　这样就得到了离散化及线性化处理后的适合进行卡尔曼滤波运算的函数表达式，可以代入EKF算法进行迭代运算。

　　3 EKF建模与DTC系统仿真

　　本文的仿真和建模是在Matlab7.O的Simulink环境下完成的，主要包括异步电动机模型、转矩调节器、磁链调节器、磁链自控制、开关信号选择单元，其中扩展卡尔曼滤波模块是由S函数编写。

　　感应电机参数如下：定子自感Ls=0.610 8 H，转子自感Lr=0.607 9 H，定、转子互感Lm=0.593 2 H，定子相绕组电阻Rs=3.67 Ω，转子相绕组电阻Rr=2.613 Ω，转动惯量J=0.027 5kg·m2，极对数p=2。

　　为验证该系统的精、动态性能，系统空载启动，设定转速为100 rad／s，进入稳定后，在t=0.5 s时加入负载TL=5 N·m，仿真图如图2～图5所示。

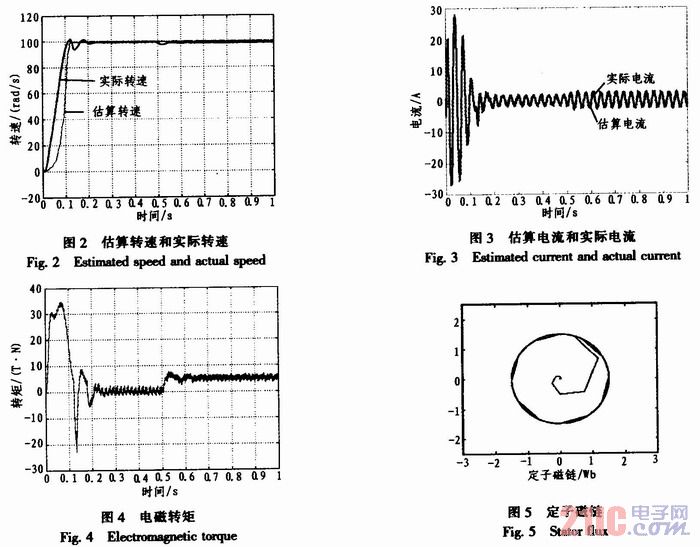
　　从仿真波形图2对比可以看出，采用无速度传感器控制算法后控制过程的上升时间比有速度传感器控制稍微长一些，但仍能满足系统性能指标要求。系统进入稳定后无速度传感器控制的效果和有传感器控制是一致的。图4显示的是突加负载后，从图3看出定子电流幅值稳定，转速变化很小并很快恢复稳定，输出转矩能很快达到给定负载转矩，体现了DTC控制系统转矩响应快的特点，由此可见电机在运行过程中，受到各种扰动时，电机转速稳定性好。

　　EKF算法在异步电机转子速度估计的应用过程中采用直接更新系统状态量和协方差矩阵的方法，可以避免直接计算值动态范围较大的增益矩阵Kk。利用EKF算法的关键在于协方差矩阵Q和R的选取。Q与模登误差、系统分布、A／D量化误差有关；R与电流传感器噪声以及A／D变换器的编码误差有关。

　　4 结论

　　从算法分析和系统仿真分析讨论的结果，可以得出扩展卡尔曼算法在无速度传感器应用中的优点是：利用扩展卡尔曼滤波器可以不必了解电机的机械参数知识（可以克服电机参数反应灵敏的问题），在电机启动过程中不必知道电机转子初始位置（可以解决电机的启动问题），此外，EKF算法可以确保系统的全局稳定性（其他一些通过状态观测器实现电机无速度传感器控制的方法，通常仅在标称状态的轨迹上将电机非线性化，不能保证系统的全局稳定性），而且整个系统易于数字化实现。但是扩展卡尔曼算法复杂，需要矩阵求逆运算，计算量大，为满足实时控制的要求，需要高速，高的数字信号处理器。另一方面，扩展卡尔曼滤波器要用到很多随机误差的统计参数，由于模型复杂，涉及因素多，使得分析这些参数的工作比较困难。