数字下变频器中坐标变换模块的ASIC应用

　　数字下变频

　　在超外差式接收机中，如果经过混频后得到的中频信号比原始信号的频率低，那么此种混频方式叫做下变频 （Down Converter or DC）。将射频信号通过或者几次的模拟下变频转换到中频上，在中频对信号数字化，然后再进行数字下变频。数字下变频（Digital Down Converter or DDC）是软件无线电的技术之一。

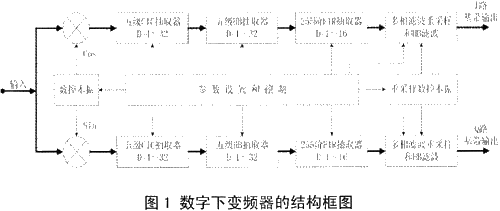
　　数字下变频结构如图1所示。可以把数字下变频分为两个基本的模块，数控振荡器：NCO（Nu-merical Control Oscillator）混频模块和抽取滤波模块。其中NCO模块产生正余弦波样本值，然后分别与输入数据相乘，完成混频。

　　抽取滤波模块常用的结构是积分梳状抽取滤波器（CIC）级联后再与多级半带滤波器（HBF）的级联。如果信号带宽比较宽，抽取倍数不是很大，可以采用FIR滤波器。当输入信号采样速率很大的时候，则可以采用多相滤波的下变频方案，把运算环节安排在抽取之后，这种结构大大降低了对数据处理速度的要求。

　　ASIC简介

　　目前，在集成电路界ASIC被认为是一种为专门目的而设计的集成电路。是指应特定用户要求和特定电子系统的需要而设计、制造的集成电路。ASIC的特点是面向特定用户的需求，ASIC在批量生产时与通用集成电路相比具有体积更小、功耗更低、可靠性提高、性能提高、保密性增强、成本降低等优点。

　　1．引言
　　数字下变频技术是软件无线电接收机的技术。其结构如图1所示。

　　本文所要阐述的就是基于CORDIC算法的数字下变频器中坐标变换模块的ASIC实现结构，该模块的主要功能是实现直角坐标系到极坐标系的变换，从而求得由I路信号和Q路信号构成的向量的幅度值和相位值，将得到的幅度信息返回给前级的数字AGC进行增益控制，还可以实现对FM信号的解调。

　　2．CORDIC算法与实现

　　2.1 CORDIC算法原理

　　CORDIC是一种迭代算法，它可以用来计算sin，cos等三角函数，计算幅值和相位等到所需的，CORDIC算法计算幅值和相位的原理如下：

　　假设直角坐标系内有向量A(Xn，Yn)，向量A顺时针旋转θn后得到向量B(Xn，Yn)，如图2所示。

　　向量A和向量B之间存在以下关系，用矩阵表示为

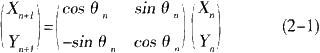
　　将cosθn提出以后得到

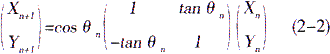
　　在这里我们取0i=arctan(1/2i)，所有迭代的总和为，其中Si={-1，+1}，则tanθi=Si2-i，可得

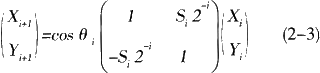
　　上式Si中的符号决定了向量的旋转方向，当时Yi≥0，Si=1，顺时针旋转；当Yi<0时，Si=-1，逆时针旋转，式中的cosθi=cos(arctan(1/2i)，随着迭代次数的增加它收敛于一个常数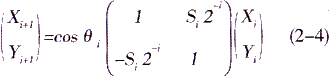，我们暂不考虑这个常数增益，这样式(2-3)就变为

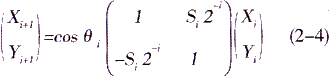
　　设总共旋转的角度为，初值为0，则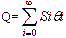，给定向量 一组初值如下

　　从上面的式子可以看出，当向量A旋转到X轴时，可以得到迭代的结果为

　　即可求得向量A的幅值和相位。由式（2-4）可知每次旋转的角度的正切值都是2的负幂次，在硬件实现时只需要执行右移和相加运算就可以实现每次迭代，易于硬件的实现。

　　2.2 用CORDIC算法的流水结构实现坐标变换

　　CORDIC迭代结构如图3所示，采用流水结构每次迭代完成旋转，每级迭代都用寄存器寄存，这样每个时钟周期都可以计算出幅度和相位。迭代的次数越多，越高，当然耗费的资源也就越多。

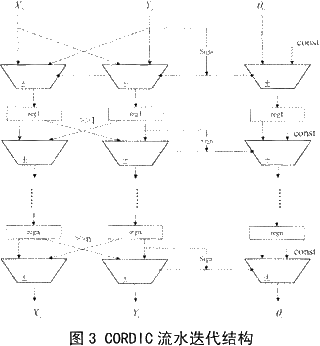
　　在数字下变频器输出I，Q两路信号后(输出信号用补码表示)，用CORDIC实现坐标变换时，为简化电路结构，只用计算的相角，其他象限的相角，采用处理后再映射的办法求取，冈此，对刚进入的数据会进行预处理。首先就是求输人数据的，并记录符号位作为处理后象限映射的依据。接下来，会判断I，Q两路数据的大小关系，并将较小的值交换到Q路，这样做的目的是要在同样的迭代次数下，达到更高的迭代。进入CORDIC迭代单元前会对I，Q两路数据进行位宽拓展，从而保证CORDIC迭代过程中，不会因截断误差造成太大的偏差。经过CORDIC迭代后所得的幅度值是有增益的，此时需要对其进行修正，另一方面，相位值需根据先前记录的I，Q两路数据的符号位和I，Q两路数据交换的情况作象限映射，表1列出了相位映射的规则。坐标变换模块的实现结构如图4所示。

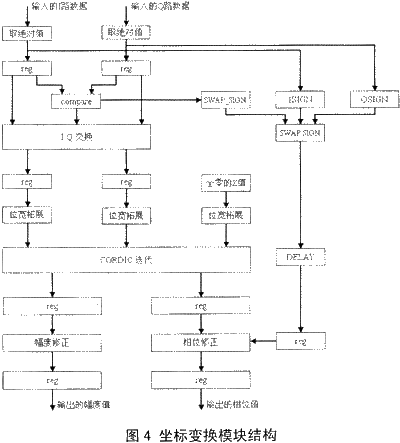
　　2.3 使用modeIsim仿真的结果

　　图5是当输入激励为I路：sin(sin2πf)；Q路：COS(COS2πf)时的modelsim仿真结果，由图中可以看出坐标变换得出的相位值是一个标准正弦信号，幅度值为恒定值，幅度相位完全正确。

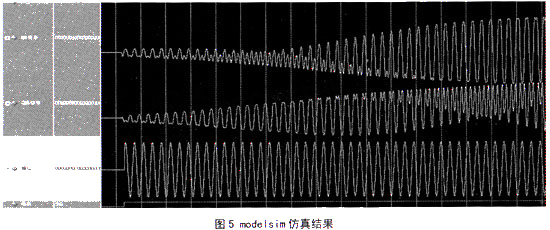
　　2.4 硬件实现结果

　　在硬件实现时，用verilog语言对坐标变换模块进行描述，为满足DDC的要求进行了18次迭代，并用DC基于UMC0.18μm的库进行了综合，硬件实现结果如图6所示。

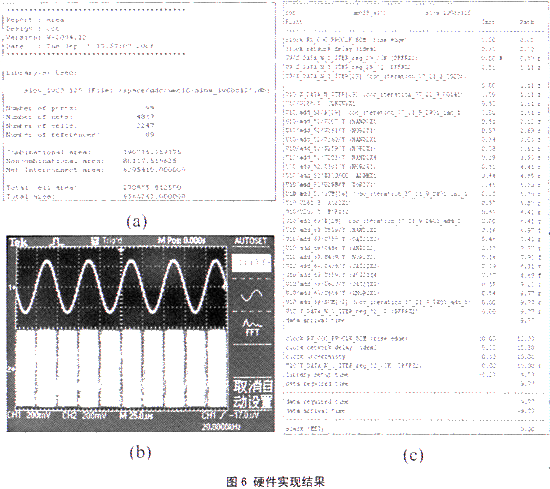
　　图6(a)是DC综合后的面积，图6(c)是关键路径的时序，综合后的路径延时为9.77ns，完全可以满足本模块数字下变频器100MHz的处理速度要求，综合出的单元(cell)的总面积仅为0.27。图6(b)是该设计在FPGA上验证的结果，该DDC的工作频率为80MHz，通道2为输入的基带信号频率20kHz，载波频率5MHz，频偏200KHz的FM信号，通道1是通过DDC下变频后交给坐标变化模块的I，O两路信号求出的相位信息，即频率为20kHz的正弦信号，由图可知该没计实现了坐标变换功能。

　　3 结论

　　使用CORDIC算法，可以获得较高的处理速度，增加迭代次数可以获得更高的处理，但会耗费较多的资源，在设计时应根据需要，合理的确定迭代次数。