一种移动机器人的路径规划算法分析

　　1 引言

　　移动机器人路径规划是机器人学的一个基本也是复杂的问题，它被描述成： 给定一个移动机器人所处的环境（环境可以通过移动机器人视觉系统或者别的途径获得），一个起始点和一个期望的终止点，移动机器人路径规划就是根据一定的任务要求寻求一条连接起始点到终止点且能避开环境中障碍物的移动机器人的运动轨迹，即或次优有效路径。

　　对机器人路径规划的研究，世界各国的学者们提出了许多不同的路径规划方法，主要可分为全局路径和局部路径规划方法。全局路径规划方法有位形空间法、广义锥方法、顶点图像法、栅格划归法；局部路径规划方法主要有人工势场法。这些方法都各有优缺点，也没有一种方法能够适用于任何场合。

　　本文提出一种短切线路径的规划方法，其涉及的理论并不高深，计算简单，容易实现，可供侧重于应用的读者参考。

　　2 短切线路径算法

　　2.1 算法基本原理

　　（1）首先判断机器人和给定的目标位置之间是否存在障碍物。如图1所示，以B代表目标位置，其坐标为（x Ｂ ，y Ｂ ），以R、A分别代表机器人及障碍物，坐标为（x Ｒ ，y Ｒ ）、（x Ａ ，y Ａ ）。这里对碰撞半径的选择作出一点说明，碰撞半径越 小，发生碰撞的危险度越大，但切线路径越短；碰撞半径越大，发生碰撞的危险度越小，但同时切线路径越长。若机器人与目标位置之间不存在障碍物，机器人可走直线直接到达目标位置，此时的直线方程可由两点式确定：

　　写成ax+by+c=0的标准形式得：

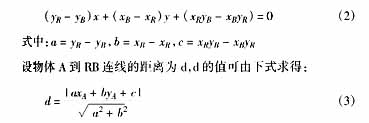
　　若d＞Ra+Rr，则机器人可沿直线到达目标点而不碰物体A，此时物体A不是障碍物。 若d＜Ra+Rr，机器人走直线可能碰上物体A，此时物体A应被视为障碍物。

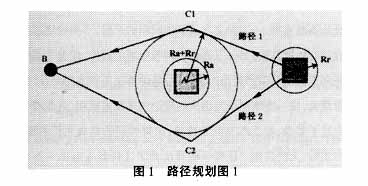
　　（2）求切线路径。如图1所示，以A点为圆心，Ra+Rr为半径作碰撞圆，其方程为：

　　k 1 ,k 2 为待求斜率，联立方程组：

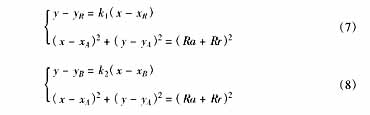
　　可分别求得两切线的斜率k 1 ，k 2 ，显然k 1 ，k 2 各有两个值，分别对应两条切线方程。两组切线两两相交，由方程组

　　求得两个交点Ｃ1、Ｃ2，称为绕过障碍物A的中途点。由此可以得到绕过障碍物A并到达目标点B的两条切线路径，路径1：R→Ｃ1→Ｂ；路径2：R→C2→B。比较两条路径的长度，在图1中，｜ＲＣ 1 ｜＋｜ＢＣ 1 ｜＜｜ＲＣ 2 ｜＋｜ＢＣ 2 ｜，可知，路径1为短切线路径。

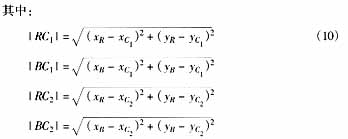
　　2.2 多障碍物情况

　　对于存在多个障碍物的情形，可分成几种情况来考虑。

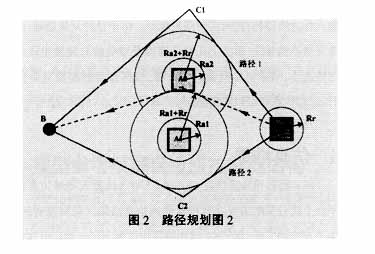
　　（1）障碍物位于前一障碍物的中途点。也就是说，机器人要到达的中途点位于另一个障碍物的碰撞圆内，如果机器人到达中途点就有可能碰上该障碍物，此时可以用该障碍物的坐标代替原障碍物的坐标来求这一侧的中途点。然后，仍然计算并比较两条路径的长度，选择短的切线路径。如图2所示，图中虚线表示原来的路径1，由于中途点被障碍物Ａ2阻挡，路径1上移。此时，｜ＲＣ 1 ｜＋｜ＢＣ 1 ｜＞｜ＲＣ 2 ｜＋｜ＢＣ 2 ｜，短切线路径应为路径2。

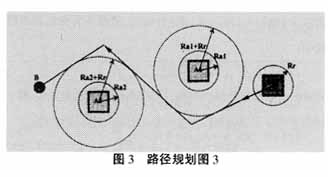
　　（2）在切线路径上存在障碍物。可把绕过多个障碍物到达终位置的任务分割成若干子任务，每个子任务要求绕过一个障碍物。这样，一个子任务就相当于前面只有一个障碍物的情况。以Ｂi、Ci分别表示第i个子任务的目标点和中途点，执行第i个子任务时，如果在到达Bi的路径上存在障碍物，则增加第i +1个子任务，此时目标点Bi+1就是Bi；如果在到达Ci的路径上存在障碍物，则增加第i+1个子任务，此时目标点Bi+1是Ci。以此类推，寻找切线路径直至到达给定的终目标位置，计算短切线路径之和即为所求的路径。图3给出了机器人绕过两个障碍物并到达目标位置的行走路径。



　　3 实际应用

　　（1）搬运机器人对于厂房车间的移动搬运机器人，切线路径规划方法是一种可行而且实用的方法。首先，机器人及障碍物的位置可以实时测得，且障碍物一般为固定不动；然后，障碍物数量固定，形状大小可预知；，搬运的效率要求机器人的行走路径为短，而且走直线比走曲线更能讲究效率。

　　（2）足球机器人Mirosot足球机器人为两轮驱动机器人。机器人足球比赛中，双方机器人以及球的坐标由悬挂在球场上方的摄像头识别并传入计算机，比赛中，机器人要把球踢进对方球门而得分。机器人首先要避开其他机器人并捉到球，根据算法，把球的坐标作为目标位置，把其他阻挡其前进路线的机器人作为障碍物，进行实时路径规划。出于目的只是避碰，而不是完全不能碰撞，碰撞半径可以尽量选小，刚好包住机器人便足够，这样做虽然碰撞危险度上升，但切线路径可以尽量缩短。

　　4 仿真结果

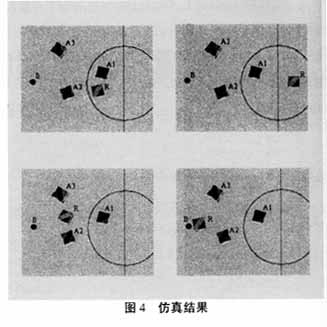
　　图4是运用该算法在Simurosot 5对5机器人足球仿真比赛平台上进行策略编程并运行得到的仿真结果。需要说明的是，为了观察的方便，例子中，球和障碍物设为固定不动。然而基于比赛过程中运动变化快速，实际效果需经长期试验观察才能看出，而且效果的好坏不但取决于算法的先进与否，在很大程度上还依赖于编程者软件水平的高低。

　　5 结论

　　移动机器人路径规划的方法有很多，可以说各有优缺点，也没有一种方法能够适用于任何场合。一个好的算法，不在于其包含的理论的高深度，而在于其实用性；理论简单，计算快捷的算法更容易被接受，关键是要看实现的效果。本文介绍的切线路径算法是一种几何方法，没有高深的理论，容易理解、便于实现，且计算简单，能够提高运行效率。不过，终运行效果还得依赖于编程水平。