在逆 F 类放大器中，集电极电压形成半正弦波，集电极电流采用方波形式。图 1 显示了基本反 F 类放大器的电路原理图。

　　二次谐波峰值放大器的电路图。

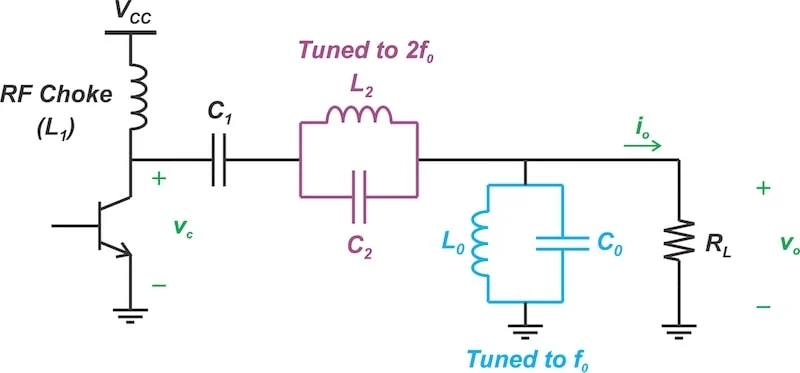
　　图 1.二次谐波峰值放大器的电路图。
　　正如我们从本系列的上一篇文章中了解到的那样，这种配置被称为二次谐波峰值放大器。然而，当我们讨论它时，我们主要关注它产生的波形。在本文中，我们将仔细地研究电路本身。然后，我们将制定二次谐波峰值放大器的基本设计方程，并使用它们来举例说明。
　　二次谐波峰值放大器的作
　　正如上一篇文章所指出的，图 1 中的原理图与三次谐波尖峰 F 类放大器的原理图几乎相同。的区别是 L2-C2谐振电路调谐到第二个谐波而不是第三个谐波。
　　一起，L2和 C2元件在二次谐波处近似于开路。但是，它们在其他谐波频率下的行为类似于短路。同样，基波谐波谐振器 （L0和 C0） 在基频处充当开路，同时在所有其他谐波处有效地将输出接地。

　　图 2 总结了负载网络在各种谐波下的阻抗。

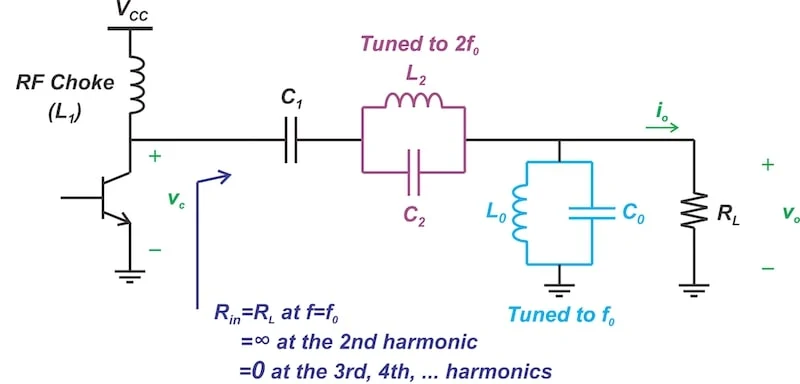
　　二次谐波峰值放大器的负载网络在不同频率下呈现的阻抗。
　　图 2.放大器的负载网络在不同谐波下表示的阻抗。
　　让我们稍微扩展一下这个总结：
　　在基频下， L2-C2谐振电路起到短路的作用，L0-C0连接近似于开路。因此，在基频下，负载网络的阻抗为RL到晶体管。
　　在二次泛音处，L2-C2连接充当开路。因此，集电极看到的是开路。
　　当谐波频率超过秒时，两个谐振电路都充当短路。因此，负载网络有效地向晶体管造成短路。
　　电压对接RL是正弦波形，因为 L0-C0TANK 使除基本电流分量外的所有组件短路。L 两端的电压2-C2tank 是二次谐波处的正弦信号，因为 L2-C2连接在该频率下为输出电流提供高阻抗。由于集电极电压是负载 （RL） 电压和 L 两端的电压2-C2tank 电路中，会向其添加二次谐波分量。
　　集电极电压和电流波形
　　反 F 类放大器的目标波形如图 3 所示。

　　反向 F 类放大器中的理想集电极电压和集电极电流波形。

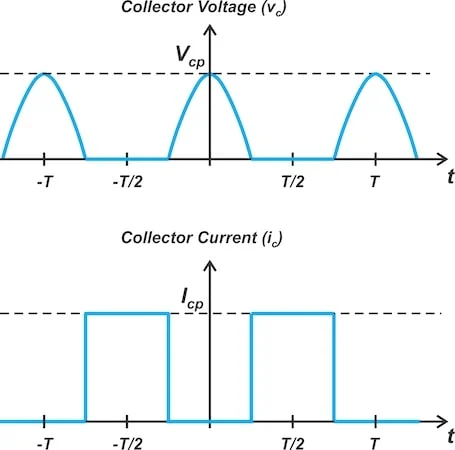
　　图 3.理想反 F 类放大器中的集电极电压 （顶部） 和电流 （底部） 波形。
　　正如我们在上面看到的，集电极电流是一个方波。为了产生此波形，二次谐波峰值级需要方波驱动信号。
　　同时，目标集电极电压波形为半正弦波。因为它只包含二次谐波，所以第二次谐波峰值放大器产生的集电极电压只能近似于此电压。集电极电压可以表示为：
　　$$v_{F} ~=~ V_{cc} -A_1 \cos（\omega_0 t）~+~A_2 \cos（2 \omega_0 t）$$方程 1.
　　对于平坦的波形，基波和二次谐波应满足以下条件：
　一个1 = 43Vcc和一个2 = 13Vcc　　方程 2.
　　图 4 绘制了二次谐波峰值放大器的平坦集电极电压波形。
　　逆 F 类放大器的平坦集电极电压波形。
　　图 4.二次谐波峰值放大器的平坦集电极电压以蓝色显示。
　　二次谐波峰值放大器的集电极电压为地。但是，平坦电压波形可以达到以下峰值：
　　$$V_{c，max}~=~\frac{8}{3}V_{cc}~\approx~2.67V_{cc}$$方程 3.
　　计算输出功率
　　现在我们已经确定了基波电压分量的幅度，让我们计算一下传递给负载的平均功率：
　　$$P_L~=~ \frac{（v_{o， rms}）^2}{R_L}~=~ \frac{1}{2}\frac{ A_1^2}{R_L} \quad \rightarrow \quad P_L ~=~ \frac{8}{9} ~\times~ \frac{V_{cc}^2}{R_L}$$方程 4.
　　这比 B 类平台的输出功率高出约 78%，B 类平台的输出功率由下式给出：　PL = 12 × V2ccRL
　　方程 5.
　　计算放大器的效率
　　要计算放大器的效率，我们需要确定输出功率 （PL来自公式 4）和从电源获取的功率 （P抄送).为了计算电源提供的功率，我们找到从电源汲取的电流的平均值 （我C、大道） 并将其乘以电源电压：
　　$$P_{cc} ~=~ V_{cc} I_{c，ave}$$
　　方程 6.
　　如图 3 所示，集电极电流是一个在 0 和我CP.通过采用傅里叶级数表示法，通过晶体管的方波电流可以表示为其频率分量之和：
　　$$i_c ~=~ \frac{I_{cp}}{2}~-~\frac{2I_{cp}}{\pi} \cos（\omega_0 t）~+~\frac{2I_{cp}}{3 \pi} \cos（3 \omega_0 t）~-~\frac{2I_{cp}}{5 \pi} \cos（5 \omega_0 t）~+~...$$方程 7.
　　信号的傅里叶级数表示表示表明，从电源汲取的直流电流为 0.5我CP.因此，公式 6 可得出：
　　$$P_{cc} ~=~ V_{cc} I_{c，ave}~=~ \frac{ V_{cc} I_{cp}}{2}$$方程 8.
　　我们可以应用公式 4 和 8 来确定放大器的效率，但前提是我们建立了我CP和V抄送.从公式 7 中，我们观察到基波分量的幅度为 2我CP/π.该电流通过负载 （RL），导致基波电压幅度为 A1= 4V抄送/3.由此，我们推断出以下内容：　2我cpπ × RL = 43Vcc→我cp = 2π3 × VccRL
　　方程 9.
　　将公式 8 和 9 结合起来，提供给放大器的功率为：　Pcc = π3 × V2ccRL
　　方程 10.
　　，我们使用公式 4 和 10 来计算效率：
　　η = PLPCC = 89 × V2ccRLπ3 × V2ccRL = 83π = 84.9 %　　方程 11.
　　需要注意的是，效率和输出功率都不能完整评估功率放大器的性能。例如，B 类级中的峰值集电极电压为 2V抄送.在我们一直在研究的逆 F 类阶段，它是 2.67V抄送.这意味着二次谐波峰值放大器的高输出功率是以晶体管上的更大电压应力为代价实现的。
　　输出功率能力
　　为了评估输出功率，同时考虑晶体管上的电压和电流应力，我们使用了一个称为输出功率能力的参数。对于功率放大器，此参数定义为：
　　$$C_p ~=~ \frac{P_{L， max}}{N I_{c， max}V_{c， max}}$$方程 12.
　　哪里：
　　PL，max是输出功率
　　我c，是集电极电流
　　Vc，是集电极电压
　　N 是放大器中的晶体管数量。
　　输出功率能力是当器件的峰值集电极电压为 1 V，峰值集电极电流为 1 A 时产生的输出功率。请注意，输出功率等于P抄送乘以效率 （η），我们可以将方程 12 改写为：
　　$$C_p ~=~ \frac{P_{L， max}}{N I_{c， max}V_{c， max}}~=~ \frac{\eta P_{cc}}{N I_{c， max}V_{c， max}}~=~\frac{\eta}{N} ~\times~ \frac{ I_{c，ave}}{I_{c， max}} ~\times~ \frac{V_{cc}}{ V_{c， max}}$$方程 13.
　　正如我们在公式 3 中看到的，二次谐波峰值放大器的平坦电压波形的峰值为 8V抄送/3.从公式 7 中我们还知道，平均集电极电流与其值之比为 0.5。将这些值代入方程 13 中，我们得到：
　　$$C_p ~=~ \frac{\eta}{N} ~\times~ \frac{ I_{c，ave}}{I_{c， max}} ~\times~ \frac{V_{cc}}{ V_{c， max}}~=~ \frac{\frac{8}{3\pi}}{1} ~\times~ \frac{1}{2} ~\times~ \frac{V_{cc}}{ \frac{8}{3} V_{cc}} \quad \quad \rightarrow \quad C_p ~=~0.159$$方程 14.
　　相比之下，B 类级的输出功率能力为Cp= 0.125 的这表明反向 F 类级为相同的晶体管规格提供更高的输出功率。
　　示例：设计二次谐波峰值放大器
　　假设我们正在设计一个反 F 类放大器，具有二次谐波峰化和平坦的集电极电压。如果电源电压为V抄送= 30 V，请确定以下内容：
　　负载电阻 （RL），输出功率为PL= 50 W，如果电源电压为 30 V。
　　晶体管必须承受的电流和电压。
　　让我们从负载电阻开始。将给定的输出功率和电源电压值代入公式 4，得到：
　PL = 89 × V2ccRL→50 = 89 × 302RL
　　方程 15.
　　它产生RL= 16 Ω.
　　从公式 3 中我们知道，此类放大器的集电极电压为：
　　$$V_{c，max} ~=~ \frac{8}{3} ~\times~ V_{cc} ~=~ \frac{8}{3} ~\times~ 30~=~80 ~\text{V}$$方程 16.
　　，根据公式 9，集电极电流由下式给出：
　　我cp = 2π3 × VccRL = 2π3 × 3016 = 3.93 一个　
　　方程 17.