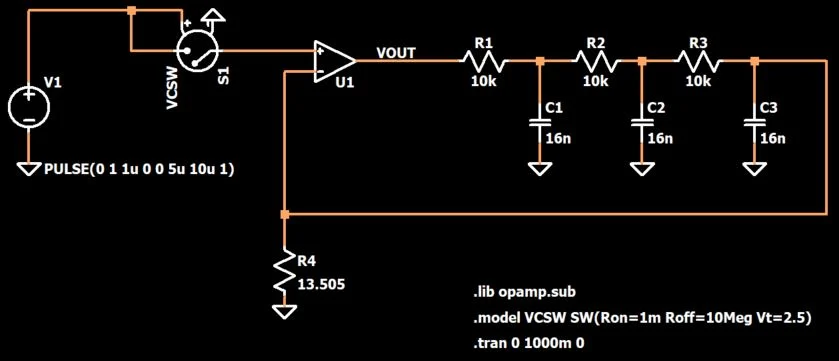
该版本使用三个高通阶段。对于我的 LTspice 模拟，我创建了一个基于三个低通阶段的修改实现：

　　关于该主题的篇文章解释了电路的一般功能，但我们仍然有一些问题需要解决：
　　振荡频率由什么决定？
　　如何分析和理解频率响应和稳定性特性？
　　理论上，通过将 R4 设置为完美值可以获得稳定的振荡，但这在现实生活中永远行不通。为了将该电路变成一个实用的振荡器，我们需要加入一个限制器。
　　振荡频率
　　正如您在上面的电路中看到的，相移振荡器包括三个 RC 低通滤波器，每个滤波器的 R = 10 kΩ 和 C = 16 nF。每个 RC 级的截止频率为 994 Hz（称为 1 kHz）。如果这也是振荡频率，那就非常方便了，但事实并非如此。

　　让我们暂时忘记相移振荡器，只考虑这个三 RC 级低通滤波器的频率响应：

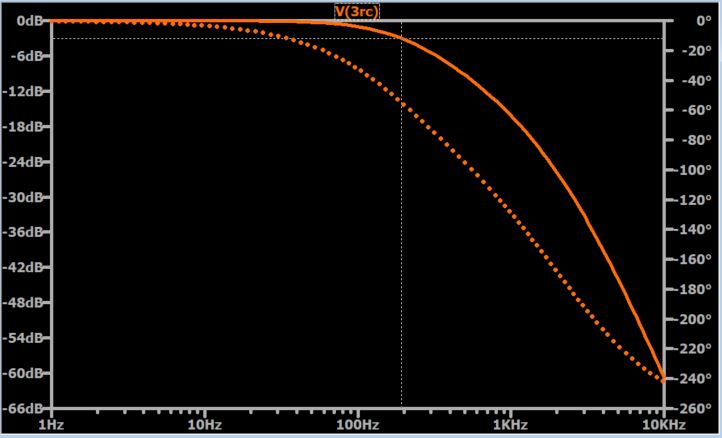
　　如您所知，截止频率的另一个名称是 –3dB 频率。如图中的光标所示，该滤波器的 –3dB 频率远不接近 1 kHz。发生这种情况是因为这三个阶段相互作用；由三个级联 1 kHz RC 滤波器组成的电路与一个三阶 1 kHz 滤波器不同。因此，您不能仅通过设置各个 RC 级的截止频率来选择振荡频率。如果您想知道，整个三级电路的截止频率也不是振荡频率。
　　重要的是要记住，截止频率不是这里的关键参数。正如上一篇文章所讨论的，关键参数是相移。如果该频率下的环路增益大于 1，则振荡会发生在 180° 相移 (f 180 )的频率处。

　　下图中的光标显示三 RC 级滤波器的 f 180 ≈ 2.5 kHz。

　　那么2.5kHz是振荡频率吗？嗯，不。问题是三级 RC 级滤波器并不是孤立存在的。它连接到运算放大器并包含在负反馈路径中，因此振荡频率由该反馈网络与放大器本身的频率相关行为的相互作用决定。
　　稳定性分析
　　为了更好地理解该电路的振荡行为，我们需要执行一些基于环路增益的稳定性分析。如果您不知道我在说什么，您应该阅读我关于稳定性的文章 ，然后阅读下一篇关于 增益裕度和相位裕度的文章。 （或者更好的是，阅读整个负面反馈系列。）
　　重要的是，我们要模拟 A（即运算放大器的开环增益）和 β（即反馈网络的频率响应），然后我们将在数学上将它们组合成环路增益Aβ。这是我们将使用的电路：
　　反馈响应 β 等于反馈电压除以开环输出电压（当我说“反馈电压”时，我的意思是如果电路处于闭环状态，则反馈到运算放大器的电压配置而不是开环配置）；因此，“V(开环)*(V(反馈)/V(开环))”相当于环路增益Aβ。
　　这是上述电路的图。
　　光标显示 180° 相移发生在 ~1.8 kHz 处。我们终于找到振荡频率了吗？
　　是的！这确实是相移振荡器振荡的频率；然而，当前电路不会振荡，因为环路增益的幅度小于 f 180处的单位。
　　通过时域实验，我发现当 R4 约为 13.5 Ω 时，振荡会从过阻尼过渡到欠阻尼。换句话说，如果R4小于13.5Ω，振荡将逐渐消失。如果 R4 大于 13.5 Ω，振荡幅度将增加（直到电路饱和）。这意味着 13.5 Ω 的 R4 值应该创建一个频率响应，其中环路增益幅度非常接近 f 180处的单位，这正是我们在下图中发现的，我通过重新模拟获得R4 = 13.5 Ω。
　　光标标记相移为 180° 的频率，如您所见，该频率下的幅度响应非常接近 0 dB。
　　添加限制器
　　我们已经在上一篇文章中介绍了限制器电路，因此我现在真正需要做的就是向您展示终电路，即基于低通滤波器的相移振荡器与限制器的结合。不过，首先我们应该解决一个问题：我们为 R4 选择什么值？
　　实际上，我们不想使用理想值，因为如果环境或操作变化导致环路增益幅度略有下降，振荡就会过阻尼。我们想要一个稍微欠阻尼的电路，以便即使环路增益有所变化，振荡也能可靠地启动并保持其幅度；饱和不会发生，因为我们有限制器来控制一切。然而，需要注意的是，您不希望电路过度欠阻尼——限制器仍会防止饱和，但终波形会出现更多失真。
　　这是电路：
　　点击放大。
　　这是生成的正弦曲线：
　　缩小视图确认振幅是稳定的：
　　我鼓励您 LTspice 文件并尝试不同的 R4 值。如果您查看 FFT，您会清楚地看到 R4 的值越高，正弦曲线的谐波失真就越高。您还将看到（遗憾的是）限幅器电路影响频率响应，使得终电路产生的振荡频率更加难以预测。