如何分析并联
电阻电路?没有欧姆定律如何计算支路电流?
在本文中,我们将介绍一些概念,这些概念将帮助您进行电路分析,而您可能不知道并联电阻网络上的电压。
并联电阻回顾
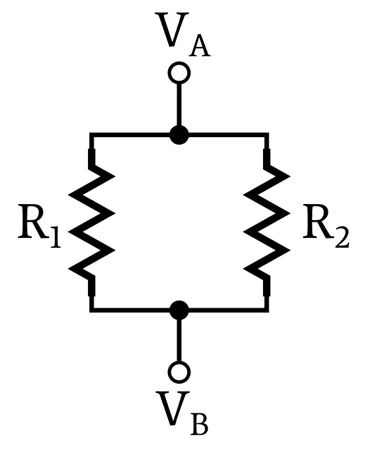
当两个电阻连接在相同的两个节点之间时,它们是并联的。并联的电阻具有相同的压降,但流过这些电阻的电流不一定相同。 电并联电阻并不总是看起来像两条平行线。下图是并联电阻网络的示例。
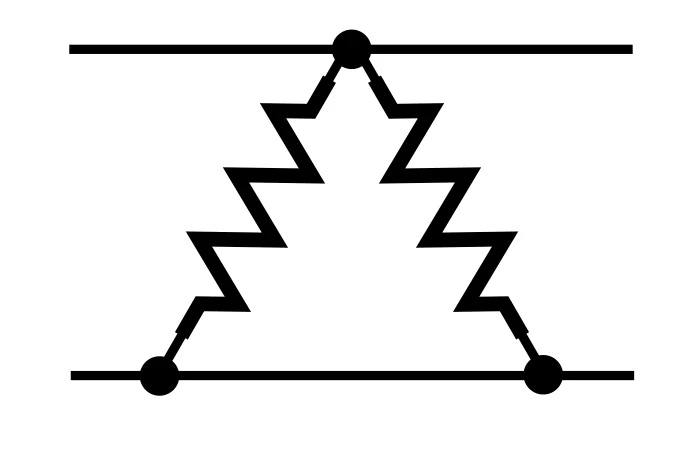
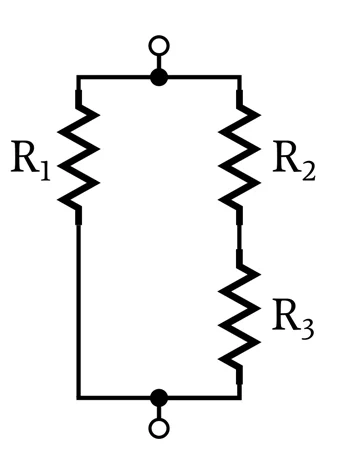
各个电阻器可以并联,但从更一般的意义上来说,一个电阻源可以与另一个电阻源并联。下图中,一个电阻与两个电阻组成的电阻并联。
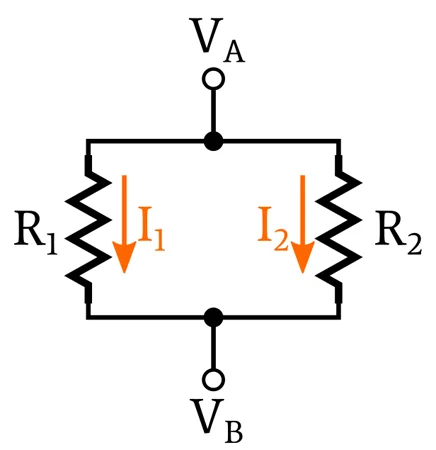
从一个节点通向另一个节点的每条当前路径称为分支。下图中,I 1和I 2是支路电流。
有关并联电阻的更多信息,请阅读本系列的篇文章。
计算支路电流
流经并联电阻器的电流受欧姆定律支配,该定律规定电压 (V) 等于电流 (I) 乘以电阻 (R)。
$$V=
IR$$
如果我们重新排列这个方程以求解电流,我们有
$$I=\frac{V}{R}$$
因此,一旦我们知道并联网络上的电压,我们就可以通过将电压除以支路电阻来计算每个支路中流动的电流。 让我们看一个例子:
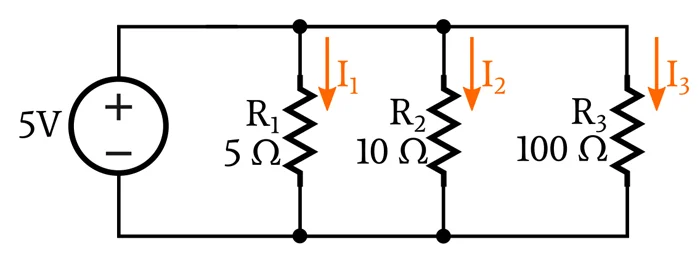
由于该电路不包含任何将并联网络与电压源分开的组件,因此我们知道网络两端的电压为 5 V。因此,我们可以通过插入每个支路的电阻值来计算三个支路电流。
$$I_1 = \frac{5\ V}{5\ \Omega}=1\ A\ \ \ \ \ \ \ \ I_2 = \frac{5\ V}{10\ \Omega}=0.5\ A\ \ \ \ \ \ \ \ I_3 = \frac{5\ V}{100\ \Omega}=0.05\ A\ \ \ \ \ \ \ \ $$
并联网络的等效电阻 接下来,我们计算以下电路的支路电流。
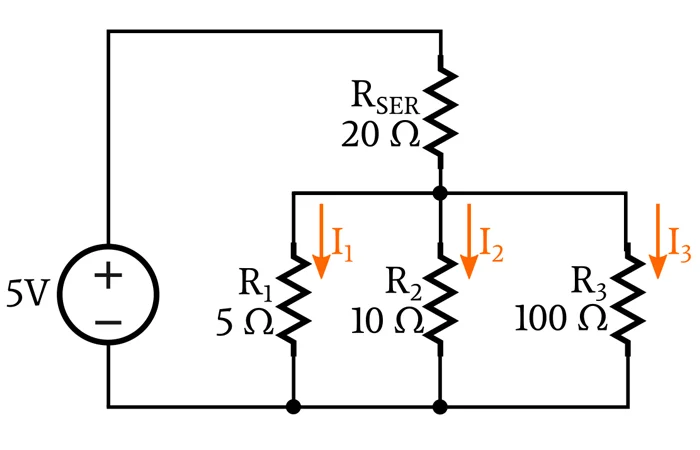
我们立即发现这种配置更难分析。为了计算支路电流,我们需要知道并联网络上的电压 (V PAR )。在前面的电路中,V PAR等于
电源电压,但在该电路中,我们无法立即确定 V PAR的值,因为部分电源电压在与并联网络串联的R SER上下降。 。如果我们知道 V RSER,我们就可以找到 V PAR:
$$V_{PAR}=5\ V-V_{RSER}$$
但为了计算 R SER两端的电压,我们需要知道有多少电流流过 R SER,并且我们无法计算 R SER的电流,因为我们不知道 I 1、 I 2的值,和我3。我们该如何进行?
这就引出了一个非常重要的概念,即等效电阻。如果我们有兴趣了解并联网络在被视为统一电气系统时的行为方式,我们可以用一个电阻器代替并联电阻器。然后我们可以使用这个等效电阻(R EQ )来分析电路,流经 R EQ 的电流将等于流经整个网络的电流:
$$I_{REQ} = I_{总计}= I_1+I_2+I_3$$
计算等效电阻
任何并联网络的等效电阻可以计算如下:
$$R_{EQ}=\frac{1}{\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\frac{1}{R_4} + \ ...}$$
当只有两个并联电阻时,还可以使用以下公式:
$$R_{EQ}=\frac{R_1\times R_2}{R_1+R_2}$$
这个等效电阻值与并联网络不完全相同;你不能用一个电阻代替两个(或三个、十个)电阻并说电路完全相同。
然而,等效电阻确实准确地复制了网络的整体电气特性。这意味着您可以使用 R EQ来确定流经支路的总电流,而该总电流可以帮助您确定并联网络上的电压。
等效电阻电路分析
让我们将等效电阻的知识应用到上面所示的四电阻电路中。首先,我们找到 R EQ。
$$R_{EQ}=\frac{1}{\frac{1}{5\ \Omega}+\frac{1}{10\ \Omega}+\frac{1}{100\ \Omega}}\约3.2\ \欧米茄$$ 现在,如果我们用单个等效电阻替换并联网络,电路将如下所示:
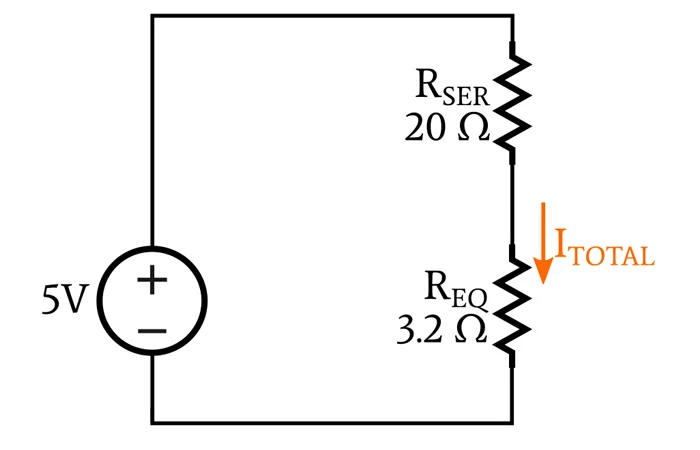
我们可以使用欧姆定律来计算 I
TOTAL:
$$I_{总计}=\frac{5\ V}{20\ \Omega+3.2\ \Omega}=0.216\ A$$
再次应用欧姆定律,我们可以计算网络电压如下:
$$V_{PAR}=I_{TOTAL}\times R_{EQ}=0.216\ A\times3.2\ \Omega=0.69\ V$$
现在我们可以像个示例中那样计算支路电流。
\[I_1 = \frac{0.69\ V}{5\ \Omega}=0.138\ A\ \ \ \ \ \ \ \ I_2 = \frac{0.69\ V}{10\ \Omega}=0.069\ A\ \ \ \ \ \ \ \ I_3 = \frac{0.69\ V}{100\ \Omega}=0.0069\ A\]






