如何设计补偿器欠压模式控制。在本文中，我们将研究如何补偿峰值电流模式控制的正激型转换器。与过压模式控制相比，峰值电流模式控制具有一些优势，包括固有的电流限制，因为它可以提供更好的线路调节并且更容易在多个功率级之间共享电流[1]。
　　目前，我们仅关注硬开关非隔离转换器和此处介绍的设计方法，该方法可适用于所有在峰值电流模式控制下无需光耦合器的正向型转换器。我们将在后面的文章中讨论隔离和其他拓扑。
　　峰值电流模式控制
　　在开始补偿器设计之前，让我们首先了解一下峰值电流模式控制 (PCMC) 的工作原理。

　　乍一看，转换器的操作非常简单。 PCMC降压转换器的电路如图 1 所示。

　　降压转换器的 PCMC
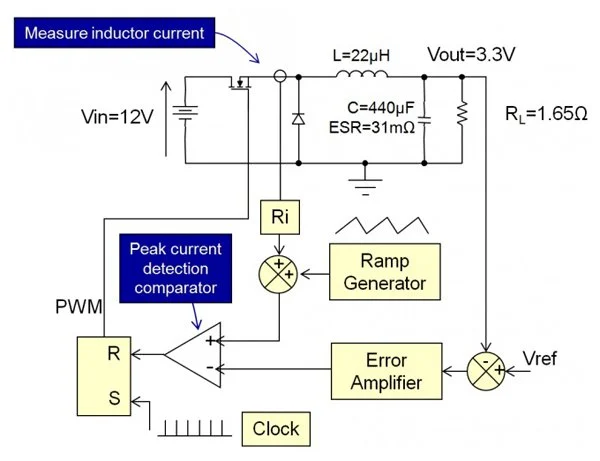
　　图 1：降压转换器的 PCMC
　　正如您所看到的，该降压转换器中的开关由置位复位触发器/锁存器控制。在开关周期开始时，时钟脉冲将 SR 锁存器的输出设置为高电平。这会以时钟频率打开开关，因此，这就是我们的开关频率。
　　使用 PCMC，我们通常测量开关电流。该峰值与按电流检测增益 Ri 缩放的电感器电流峰值相同。如果有电源变压器，那么当然，这也会缩放电流。从图 1 中可以看出，该信号被馈送到峰值电流检测比较器。比较器的另一个输入是电流峰值的需求值。
　　换句话说，我们正在将我们想要的电流（我们的需求电流）与我们实际获得的电流（我们的测量电流）进行比较。一旦实际测量的电流等于我们想要的电流，比较器电路的输出就会变高，重置锁存器，从而关闭开关。在下一个周期中，我们的需求电流可能会发生变化，这意味着一旦实际电流达到新的需求值，我们就会关闭开关。因此，我们正在控制电感器电流的峰值。
　　但是，我们如何设置电流的需求值呢？再次查看图 1，我们可以看到，我们还有一个由误差放大器及其补偿组件形成的电压环路。我们电路这部分的输出产生了电流的需求值。
　　简而言之，我们将实际输出电压与需求输出电压进行比较，两者之间的误差或差异（电压环路补偿后）设置了我们的电流需求值。因此，我们的工作是计算极点和零点，从而计算该补偿器的元件值。
　　次谐波振荡和斜率补偿
　　我们在图 1 中没有讨论的一部分是斜坡发生器块。如果我们将输入电压设置为值，将负载设置为值，然后在示波器上查看 PWM，并看到 PWM 占空比轨迹反复从粗脉冲到细脉冲再到粗脉冲，那么我们的转换器将经历次谐波振荡。这是当前模式令人头疼的问题之一。
　　无需讨论太多细节，问题是在电流模式下，在开关频率 Fs [2] 的一半处实际上存在一对复共轭极点，因此在该频率下，我们将产生谐振凸点；如图 3 中的绿色虚线所示。随着占空比的增加，该双极点的 Q 值也会增加，直到某个点增益将以一半开关频率穿过 0 dB 轴，从而导致次谐波振荡，即不稳定。
　　为了避免这种情况，我们需要做的就是在测量的电流中添加一个斜坡，这样，如果发生这些振荡，开关就会比其他情况更早关闭（如图中的红色虚线区域所示） 2）。这将抑制任何次谐波振荡并导致它们衰减。这是图 1 中的斜坡发生器块的工作。请注意，在许多现代芯片中，此斜坡是在内部添加的，因此您不必自己添加它。
　　峰值电流模式补偿器设计
　　对于峰值电流模式控制，我们使用的误差放大器通常是 II 型补偿器。 II 型补偿器的电路如图 2 所示。极点和零点由补偿器周围反馈网络中的电容器和电阻器设置。我们之前的文章中已经介绍了这种补偿器类型以及极点和零点的概念。

　　II型补偿器

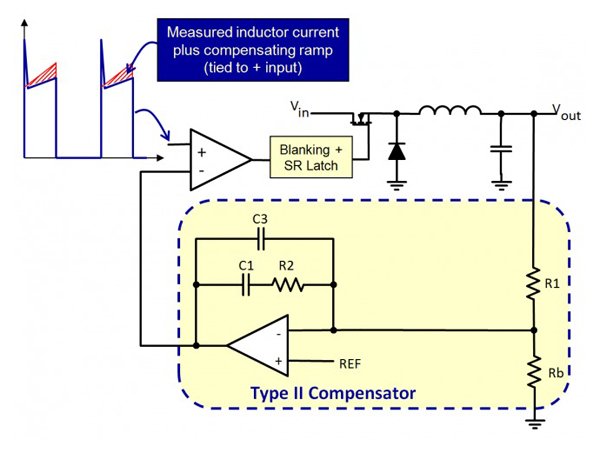
　　图 2 – II 型补偿器
　　从之前的文章中，我们知道传递函数 Hc(s) 以及极点和零点与元件值的关系方程如下：
　　`H_c(s)=(\omega_(CP0)/s)*((s/\omega_(CZ1)+1)/(s/\omega_(CP1)+1))`
　　公式1
　　这里 wcp0 和 wcp1 是补偿器的极点，wcz1 是补偿器的零点。我们的工作是计算它们，以便我们可以根据下面的方程计算组件值。请注意，这些极点/零点以弧度每秒为单位，但我们通常以赫兹为单位，因此请不要忘记在需要时转换它们。
　　`\omega_(CP0)=1/(R_1*(C_1+C_3))`
　　`\omega_(CP1)=(C_1+C_3)/(R_2*C_1*C_3)`
　　`\omega_(CZ1)=1/(R_2*C_1)`
　　Biricha Digital 的自动化电源设计软件 (Bricha WDS) 可自动设计优化的补偿器，如之前的文章所述。但是，如果您的瞬态响应要求不是很严格，您可以按照下面列出的步骤为正激拓扑设计合理且稳定的补偿器。
　　以下是有关如何快速设计该转换器补偿器的分步指南。我们需要的所有值如图 1 所示。
　　第 1 步：确定所需添加的斜坡量
　　如果您的芯片没有内部斜坡生成功能，许多工程师会根据经验计算出要添加的斜坡量，即将转换器设置为占空比并添加足够的斜坡，直到不发生振荡。或者，您可以使用以下等式计算所需的斜率补偿量（添加到感测电流的补偿斜坡的峰峰值高度），该等式对所有正激型转换器都有效，并且基于 [2]。
　　V PP =(1 π 0.5+ D ) R i  T s V in n 2 L
　　公式2
　　其中 D 是我们的稳态占空比，Ri 是我们的电流感应增益，Ts 是开关周期，Vin 是我们的输入电压，n 是我们的变压器匝数比（对于降压转换器设置为 1），L 是输出电感。
　　这将产生以开关频率一半阻尼一对复共轭极点的效果，从而使它们的 Q 值为 1。如前所述，这些极点会导致不良的次谐波振荡，而这是 PCMC 的固有特性。
　　第 2 步：确定植物波特图

　　实际上，您根本不需要绘制此图，但将正在发生的情况可视化是很好的。峰值电流模式转换器有多种型号；这里我们使用了流行的 Ridley 模型。详细的数学分析和方程请参见[2]、[3]。

　　图 3 显示了我们的 PCMC降压转换器的波特图。正如您所看到的，我们有一些低频/直流增益、一个低频实极点、一个 ESR 零点和一对半 Fs 处的复共轭极点。对于所有硬开关正激型转换器，该图的整体形状将相同。然而，设备的低频极点和 ESR 零将会不同，但复共轭极点对将始终保持在 Fs 的一半。 （请参阅第 1A 条了解我们对传递函数的讨论）。

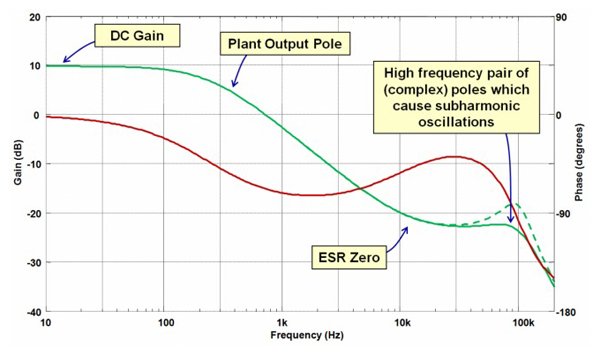
　　PCMC 降压转换器的设备级波特图。绿色迹线是增益，红色迹线是相位。
　　图 3 – PCMC 降压转换器的设备级波特图。绿色迹线是增益，红色迹线是相位。
　　绿色虚线显示了在没有斜率补偿的情况下开关频率一半时的复共轭极点。占空比越大，峰值就越明显。实心迹线显示了当我们应用步骤 1 中计算的斜率补偿时这些极点发生的情况。
　　正如您所看到的，与上一篇文章中讨论的电压模式控制不同，我们只有一个低频设备极点，后面是由电解输出电容的寄生等效串联电阻 (ESR) 形成的零。
　　步骤 3：计算 II 型补偿器极点/零点
　　这里介绍的方法是一种近似方法，可让您快速计算补偿器的极点和零点，该补偿器在合理的交叉频率（即开关频率的 1/10）下具有相对良好的性能。
　　我们的电源设计软件 (Biricha WDS) 使用算法，但是，在这篇短文中，我们将选择这种近似方法，以便您可以手动执行计算（或者可能在您喜欢的数学包的帮助下）。
　　您可以从补偿器的传递函数中看到，我们在原点有 1 个极点、1 个零极和 1 个极点。请不要忘记更改为 Hz（我们已将以下等式中的 w 更改为 f 以表示此更改）。为了获得合理的性能：
　　1 – 将 1 个补偿器极置于 ESR 零频率处以取消电站的 ESR 零：
　　`f_(CP1)=1/(2\piESRC)="11.6 kHz"`
　　公式3
　　2 – 将补偿器置于所需交叉频率的 1/5 处，以在交叉点周??围提供相位提升（请记住，零会带来相位提升 - 请参阅第 1A 条） Fx 是所需的交叉频率。在我们的例子中，让我们针对 Fx 进行设计
　　`f_(CZ1)=F_x/5="2 kHz"`
　　公式4
　　3 – ，我们将极点放置在公式 5 中给出的频率处的原点处。
　　`f_(cp0)=(A_1*A_2*A_3)/(2*\pi*n*L*R_L)`
　　公式5
　　其中 A1、A2 和 A3 是：
　　`A_1=1.23*F_x*R_i*(L+(R_L*T_S)/\pi)`
　　`A_2=sqrt(1-4*F_x^2*T_s^2+16*F_x^4*T_s^4)`
　　`A_3=sqrt(1+(4*\pi^4*C^2*F_x^2*L^2*R_L^2)/(L*\pi+R_L*T_S)^2)`
　　请不要被这些大方程吓倒——里面没有我们不知道的东西。
　　计算 10kHz 交叉频率的方程得出：
　　`f_(cp0)="25.85 kHz"`
　　步骤 4：计算补偿器元件值
　　现在我们知道了补偿器极点和零点的位置，我们可以使用上面的方程来计算补偿器的元件值。
　　正如我们在上一篇电压模式文章中讨论的那样，您可以根据您愿意允许通过的电流以及控制器 IC 所需的参考电压来计算 R1 和 Rb。请参阅第 2B 条了解更多信息。通过允许 1mA 的电流通过该电位器并使用标准分压器方程和欧姆定律，我们可以计算：
　　`R_1="750"\欧米茄`
　　`R_B="2.55 k"\Omega`
　　2 – 现在我们知道了 R1，通过重新排列上面的极点和零点方程并求解分量值，我们可以使用下面的方程计算 C1、C3 和 R2 的值（请不要忘记这些方程使用极点/零点以 rad/sec 为单位，因此我们需要将它们从 Hz 转换）。
　　`C_1=(\omega_(CP1)-\omega_(CZ1))/(R_1*\omega_(CP0)*\omega_(CP1))`
　　`C_3=\omega_(CZ1)//(R_1*\omega_(CP0)*\omega_(CP1))`
　　`R_1=(R_1*\omega_(CP0)*\omega_(CP1))/((\omega_(CP1)-\omega_(CZ1))*\omega_(CZ1))`
　　评估这些方程可以得出：
　　`C_1="6.8 nF"`
　　`C_3="1.4 nF"`
　　`R_2="11.7 k"\欧米茄`

　　我们可以轻松地在“手动极点/零位放置”模式下使用 WDS 来验证我们的计算。 WDS 为我们提供了所有重要的稳定性参数以及波特图。我们设计的 WDS 波特图如图 4 所示，稳定性信息如图 5 所示。

　　Biricha WDS 的模拟环路伯德
　　图 4：来自 Biricha WDS 的模拟环路波特率
　　来自 WDS 的稳定性数据
　　图 5：WDS 的稳定性数据
　　从图 4 和图 5 中我们可以看到，我们已经实现了所需的 10kHz 交叉频率和 74 度的相位裕度。交叉点的斜率是 -20db/decade，我们的增益裕度优于 20dB。因此，我们设计了一种非常稳定的电源，具有可观的交叉频率和大相位裕度。
　　设计补偿器
　　在本文中，我们讨论了如何为所有硬开关正向型峰值电流模式转换器（无光耦合器反馈）设计补偿器。已经提出了一种近似方法，在大多数情况下可以给出相对较好的结果。
　　这里提出的方法的优点是计算速度快，但我们无法控制相位裕度。此外，我们还提供了一个完整的数值示例，直至元件值选择。