RF 模拟设计中的噪声分析
　　我们通常通过串联电压源 （\（\overline{v^{2}_{n，input}}\）） 和并联电流源 （\（\overline{i^{2}_{n，input}}\）） 来模拟电路中所有噪声源的影响，如图 1 所示。

　　串联电压源和并联电流源的电路中噪声源的影响。

　　图 1. 具有串联电压源和并联电流源的电路中噪声源的影响。
　　在图 1 中，“无噪声网络”与“噪声网络”相同，只是其组件（电阻器、晶体管等）被假定为无噪声。通过将两个电路的输出噪声相等，我们可以找到折合到输入端的噪声电压和电流源的值。对于任何源阻抗 （RS).
　　使用 OP27 运算放大器示例了解源阻抗
　　在 RF 设计中，尤其是分立 RF 设计中，我们通常更喜欢使用噪声系数概念，而不是噪声电压和电流源模型。然而，上述模型可以帮助我们更好地理解电子电路中的噪声行为以及噪声系数度量的微妙之处。
　　一个关键的观察结果是，电路的输出噪声取决于前的输出阻抗（或源阻抗 RS).这可以通过考虑 R 的极端情况来理解S= 0 和 RS趋于无穷大 （RS→ ∞).对于 RS= 0，则 \（\overline{i^{2}_{n，input}}\） 短路，对输出噪声没有影响。
　　另一方面，如果 RS趋于无穷大，则 \（v^{2}_{n，input}\） 不能产生输出噪声。图 2 显示了源电阻 （R） 对实际运算放大器 （OP27） 配置的影响。
　　源电阻对 OP27 运算放大器配置的影响。
　　图 2.源电阻对 OP27 运算放大器配置的影响。图片由 Analog Devices 提供
　　OP27 的电压噪声为 \（3\frac{nV}{\sqrt{Hz}}\），电流噪声为 \（1\frac{pA}{\sqrt{Hz}}\）。
　　在上面的示例中，仅考虑了来自源阻抗 （R） 和运算放大器的噪声。当 R = 0 时，运算放大器噪声电流源短路，总输入参考噪声由运算放大器 \（3\frac{nV}{\sqrt{Hz}}\） 的电压噪声决定。
　　当我们将源电阻增加到 R = 3 kΩ 和 300 kΩ 时，运算放大器噪声电流源预计会流过运算放大器的源阻抗和输入阻抗。然而，由于运算放大器的输入阻抗在几MΩ的范围内，噪声电流仍然主要流经源阻抗。因此，当 R = 3 kΩ 和 300 kΩ 时，噪声电流分别产生 \（3\frac{nV}{\sqrt{Hz}}\） 和 300 \（\frac{nV}{\sqrt{Hz}}\） 的等效噪声电压。

　　当 R = 3 kΩ 和 300 kΩ 时，运算放大器的噪声电压仍然在运算放大器输入端产生 \（3\frac{nV}{\sqrt{Hz}}\），因为与运算放大器输入阻抗相比，这些电阻值相对较小。

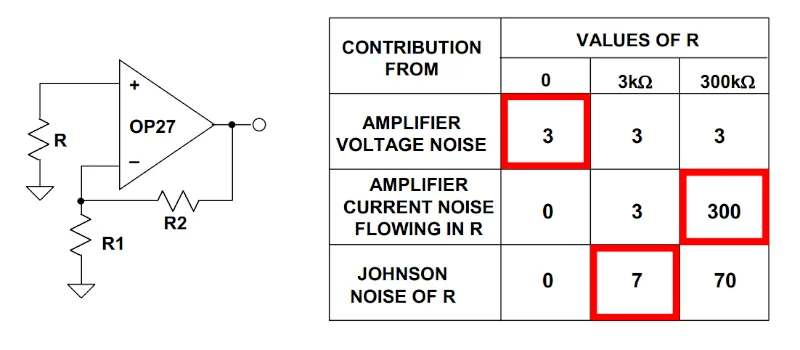
　　图 2 中的表格还给出了所考虑的三个不同值的 R 热噪声。可以看出，主要的噪声源（在图 2 的表格中用红色矩形突出显示）以及因此，电路的整体噪声性能随源阻抗而变化。这是使用 noise figure 度量时要记住的一个重要概念（稍后将讨论）。
　　需要替代 Noise 指标
　　折合到输入端的噪声发生器模型不适合 RF 设计。例如，在计算 RF 增益级的输入参考噪声电流时，我们需要测量该级在目标频率下的跨阻。在高频下，此类测量非常具有挑战性。因此，找到另一个在高频下更容易测量的噪声性能指标。
　　此外，在许多射频系统中，我们对信号功率与噪声功率的比率（SNR 或信噪比）感兴趣。SNR 指定了信号的质量，并终决定了我们的通信系统接收到的数字比特中有多少是错误的（系统的误码率）。
　　所需的 SNR 取决于多种因素，例如：
　　调制方案
　　比特率
　　每个比特的能量
　　筛选带宽

　　大多数数字通信系统需要至少 10 dB 的 SNR。SNR 是在接收器系统的输出端测量的，在那里执行解调。如图 3 所示，典型的接收器信号链由几个不同的模块组成，例如低噪声放大器 （LNA）、混频器、滤波器和模数转换器 （ADC）。

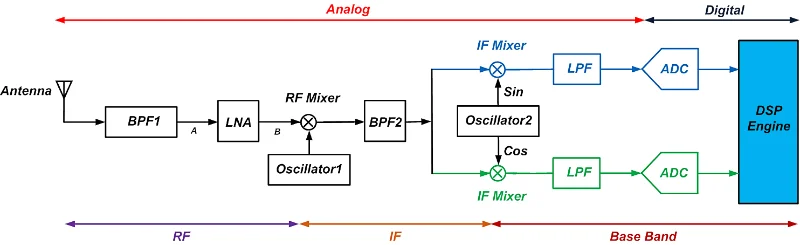
　　图 3. 接收器信号链框图示例。
　　RF 工程师需要了解这些电路元件中的每一个如何影响噪声性能，以及当信号通过信号链时 SNR 如何降低。因此，与 SNR 直接相关的噪声性能指标在 RF 设计中可能更有帮助。这就是噪声系数规格的突出之处，因为噪声系数可以在高频下更容易测量，并且直接基于 SNR 规格定义。
　　噪声因数和噪声系数测量
　　电路的噪声因数 （F） 定义为输入端的 SNR 与输出端的 SNR 之比：
　　\[F=\frac{SNR_{in}}{SNR_{out}}\]
　　方程 1.
　　在上述公式中，噪声和信号功率量以线性项表示，而不是以分贝表示。以分贝表示的噪声因子称为噪声系数 （NF）：
　　\[NF=10log_{10} \big（ \frac{SNR_{in}}{SNR_{out}} \big）\]
　　方程 2.
　　应该注意的是，一些参考文献没有进行这种区分，而是使用术语噪声系数来指代公式 1 和 2。在这种情况下，我们应该从上下文中确定噪声系数是用分贝还是线性项表示。
　　对于无噪声电路，输入和输出 SNR 相同，导致 F = 1 和 NF = 0 dB。噪声系数是电路引起的 SNR 劣化的直接量度。例如，如果电路输入端的 SNR 为 60 dB，电路噪声系数为 7 dB，则电路输出端的 SNR 为 53 dB。更准确地说，假设电路的输入噪声功率等于计算电路 NF 的参考噪声功率，则此陈述是有效的（我们将在下一篇文章中详细讨论这一点）。
　　其他噪声系数定义
　　使用一点代数，我们可以从方程 1 中推导出有用的替代表达式。如果我们用 S 表示电路输入和输出端的信号功率我和 So，输入和输出处的噪声功率 N我和 No，我们得到以下方程：
　　\[F=\frac{\frac{S_i}{N_i}}{\frac{S_o}{N_o}}=\frac{S_i}{N_i} \times \frac{N_o}{S_o}\]
　　考虑到这一点，您可能想知道，输出信号与输入信号有什么关系？由于这些是功率量，因此我们需要考虑电路的功率增益。功率增益为 G 时，我们有 So= GS我，这导致了等式 3：
　　\[F= \frac{N_o}{GN_i}\]
　　方程 3.
　　在公式 3 中，No是输出处的总噪声。它包括电路内内部噪声源的影响以及来自源阻抗（或前的输出阻抗）的噪声。N我噪声是源阻抗 （RS） 在电路的输入端产生。从公式 3 中，噪声因子是总输出噪声除以来自源电阻的那部分输出噪声。
　　为了推导出另一个表达式，让我们关注源阻抗 N 产生的输出噪声部分o（源）、以及电路 N 内内部噪声源产生的部分o（新增）.因此，我们得到：
　　\[N_{o（source）}=GN_{i}\]
　　\[N_{o}=N_{o（源）}+N_{o（已添加）}\]
　　将这些方程代入方程 3 可得到方程 4：
　　\[F=1+\frac{N_{o（已添加）}}{N_{o（源）}}\]
　　方程 4.
　　公式 4 表明，我们得到的噪声系数值取决于源阻抗 （RS） 连接到电路。在公式 4 中，No（源）显然是 R 的函数S.但是，根据我们在上一节中的讨论，我们知道电路本身的噪声也是 R 的函数S.因此，必须根据已知的源阻抗（通常为 50 Ω）指定噪声系数。
　　计算示例电路中的噪声系数

　　在本例中，我们将使用公式 1 和 4 来计算以下电路的噪声系数（图 4）。

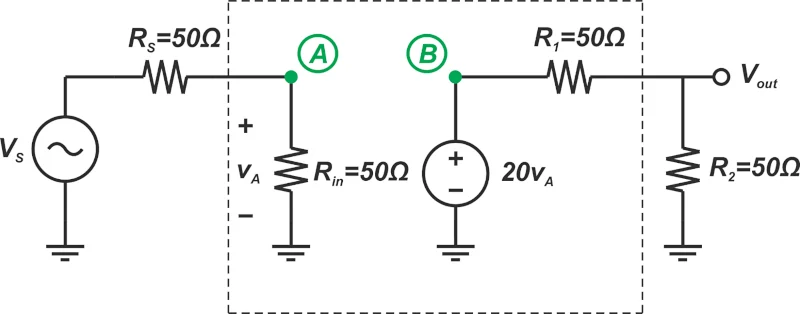
　　图 4. 示例电路。
　　我们假设输入电压的 RMS 值为 VS，所有电阻值为 50 Ω，系统的噪声带宽为 Bn= 1 兆赫。
　　要使用公式 1，我们需要计算电路输入和输出处的 SNR。由于 RS= R在，则输入信号在电路的输入端（节点 A）减半。因此，节点 A 处信号的 RMS 值为 ：
　　\[V_A=\frac{V_s}{2}\]
　　输入信号功率为：
　　\[S_i=\frac{V_A^2}{R_{in}}=\frac{V_s^2}{4R_{in}}\]
　　方程 5.
　　完成后，我们可能会问如何计算 input noise。我们知道电阻 R 的 RMS 噪声电压在 \（V/\sqrt{Hz}\） 中由下式给出：

　　\[V_{n， rms}=\sqrt{4kTR}\]

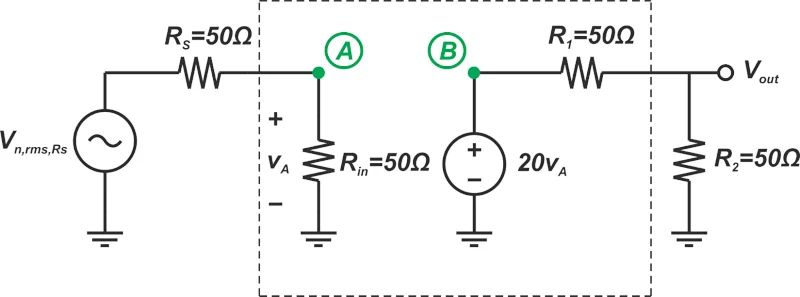
　　图 5 显示了用于计算 R 噪声的电路图S.
　　图 5. 从 R 计算噪声的示例电路图S.
　　在此图中，输入电压源短路，噪声电压 RS与该电阻器串联添加。由于 RS= R在，噪声电压 RS在输入端减半，产生输入噪声功率：
　　\[N_i=\frac{（噪声 \text{ } 电压 \text{ } @ \text{ } 输入 \text{ } 应将 \text{ }支付给 \text{ } R_S）^2}{R_{in}^2}=\frac{V_{n，rms}^2}{4R_{in}}=kT\]
　　方程 6.
　　N我是电路输入端的噪声功率。需要注意的是，N我的计算假设电路的输入阻抗 （R在） 是无噪音的。由于 Vn，rms在 \（V/\sqrt{Hz}\） 中，上述方程给出了每单位带宽的噪声功率 \（（V^{2}/Hz）\）。
　　因此，公式 6 的结果应乘以噪声带宽 Bn以求目标带宽上的总噪声功率。考虑到带宽，公式 5 和 6 给出了输入 SNR：
　　\[SNR_{in}=\frac{V_S^2}{4kTB_nR_{in}}\]
　　方程 7.
　　要计算输出信号和噪声功率，我们需要找到电路的功率增益（输出功率与输入功率的比值）：
　　\[G=\frac{P_{out}}{P_{in}}=\frac{\frac{V_{out}^2}{R_2}}{\frac{V_A^2}{R_{in}}}=\frac{V_{out}^2}{V_A^2}\]
　　方程 8.
　　在上面的方程中，V外表示输出电压的 RMS。从电路图中，我们注意到：
　　\[V_{out}=V_A \times 20 \times \frac{R_2}{R_2+R_1}=10V_A\]
　　公式 8 简化为 G=100。输出信号功率计算公式为：
　　\[S_o=GS_i=100\times \frac{V_s^2}{4R_{in}}\]
　　方程 9.
　　根据公式 6，源电阻引起的输出噪声计算如下：
　　\[N_{o（源）}=GN_i=100kT\]

　　方程 10.

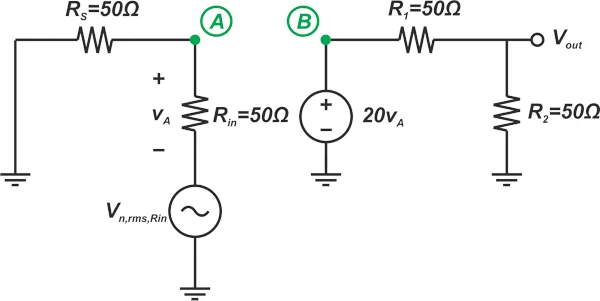
　　图 6 显示了计算 R 噪声贡献的电路图在.
　　图 6. 计算 R 噪声贡献的示例电路图在.
　　将上图与图 5 进行比较，我们可以得出结论，R 的输出噪声在与 R 中的相同S（100 千吨）。每个 R 的输出电压噪声功率1和 R2可以很容易地计算为 kT。因此，总输出噪声为：
　　\[N_{o}= N_{o， RS}+N_{o， Rin}+N_{o， R1}+N_{o，R2}=100kT+100kT+kT+kT=202kT\]
　　方程 11.
　　同样注意，公式 10 和 11 给出了每单位带宽的噪声功率 （V2/Hz），结果应乘以噪声带宽 Bn以求目标带宽上的总噪声功率。公式 9 和 11 给出了输出 SNR：
　　\[SNR_o=\frac{S_o}{N_o}=\frac{100V_s^2}{808kTB_nR_{in}}\]
　　方程 12.
　　，根据公式 7 和 12 计算噪声因子：
　　\[F=\frac{SNR_{in}}{SNR_{out}}=\frac{V_S^2}{4kTB_nR_{in}}\times \frac{808kTB_nR_{in}}{100V_s^2}=2.02\]
　　方程 13.
　　以分贝表示，我们得到 NF = 3.05 dB。现在，让我们使用公式 4 来分析电路噪声系数。在这种情况下，我们只需要计算来自源阻抗 N 的输出噪声部分o（源）以及电路 N 产生的部分o（新增）.No（新增）可以根据公式 10 和 11 计算：
　　\[N_{o（已添加）}= N_{o}-N_{o（源）}=202kT-100kT=102kT\]
　　方程 14.
　　将公式 10 和 14 代入公式 4 可得到：
　　\[F=1+\frac{N_{o（已添加）}}{N_{o（源）}}=1+\frac{102kT}{100kT}=2.02\]
　　这与前面的计算结果一致。使用公式 4，我们不需要计算输入和输出信号功率以及输入和输出 SNR。因此，方程 4 可以更容易地计算。