如果您希望设计一个涵盖音频和低射频的可调谐低失真正弦振荡器，您很可能会首先考虑几十年来教科书中出现的一些经典 RC 振荡器，例如那些在Wien 或 Bridged-T 网络。
    这些 RC 网络提供随频率变化的相移，因此在一个特定频率下，反馈回路周围的总相移为零。围绕网络的有源反馈环路的增益克服了无源 RC 网络的衰减，振荡稳定在零相移频率。
    在本文中，我们将了解这些经典网络，并讨论它们的一些局限性。
    经典振荡器网络
    在这里，我们将回顾一些围绕经典 Wien 和 Bridged-T 网络构建的振荡器的基本原理图，例如使用双联动可变电阻器进行调谐。    图 1 和图 2 显示了LA Meacham 于 1938 年引入并用于 HP 201A 的 白炽灯泡振幅稳定的有源反馈环路：

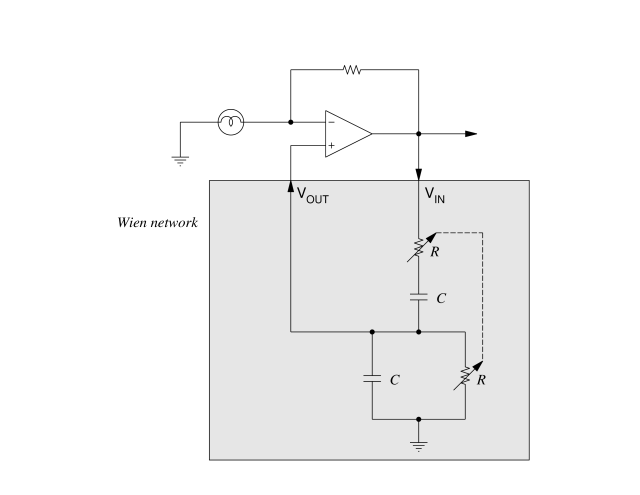
    图 1.围绕经典维恩网络构建的振荡器的基本示意图    对于 Bridged-T 网络，α是大于 1 的某个设计因子，通常为 2 到 4：

    图 2.围绕经典 Bridged-T 网络构建的振荡器的基本原理图
    通过一些电路理论，我们可以得出 Wien 和 Bridged-T 网络的零相移频率分别如下：
    维恩网络： $$f_{osc} =\frac {1}{2\pi{RC}}$$
    桥接-T 网络： $$f_{osc} =\frac{1}{2\pi\sqrt{\alpha}RC}$$
    在这些谐振频率下通过网络的衰减分别是 3 和 $$\frac{2+\alpha}{2}$$ 的因数。
    Wein 网络实现了一个带通滤波器，而 Bridged-T 网络实现了一个带阻滤波器，这种差异解释了反馈极性和灯泡放置的差异，以稳定幅度。    着眼于这些原理图中阴影框中的经典 Wien 和 Bridged-T 网络，SPICE 模拟了它们的正弦传递函数 $$\frac{V_{OUT}}{V_{IN}}$$ 的幅度和相位作为频率的函数绘制在图 3 和图 4 中。

    图 3. R=10kΩ、C=10nF 时 Wien 网络的仿真结果
    这些图中的虚线标记了绿色相位线穿过零度时的振荡频率。虚线与红色幅度线相交的点标记了反馈增益必须克服的衰减。维恩网络的衰减系数 3 在图 3 中表示为 -9.5 dB 的幅度。    Bridged-T 网络是用 $$\alpha = 4$$ 的典型值模拟的。使用这些值，共振衰减为 $$\frac{2+\alpha}{2} = 3$$，就像在 Wien 网络中一样。

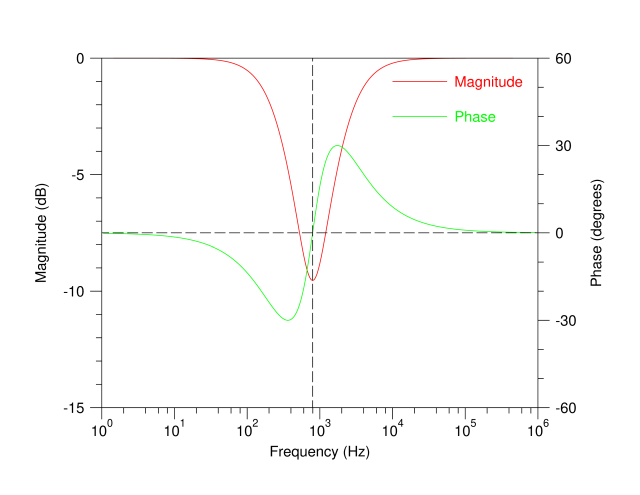
    图 4. R=10kΩ、C=10nF、α=4 的桥接-T 网络的仿真结果
    RC 振荡器电路的问题
    但在实践中很难在很宽的频率范围内调整这些经典网络。
    在所有这些电路中，至少必须改变两个电阻器或两个电容器，并且这些变化必须非常紧密地跟踪以保持网络衰减随频率变化。
    例如，在传奇的基于维恩网络的 201A 型振荡器仪器中，惠普公司使用了一个大型多节联动可变电容器来保持这种跟踪接近。双联可变电阻器较小，但在构建时非常昂贵以保持紧密跟踪。除非网络衰减在频率范围内保持恒定，否则振荡器输出幅度将在其调谐范围内变化，这对于测试仪器来说是不受欢迎的特性。