使用正弦波形的电路分析:RL 电路示例
在深入讨论之前,应该注意的是,正弦波形在解决许多工程和科学问题方面发挥着关键作用。例如,在电路分析中,了解不同频率下对正弦波形的响应,可以确定对其他类型波形的稳态响应。为了更好地理解这一特性,我们来看看图 1 所示的简单 RL (电阻-
电感)电路。 RL 电路示例。
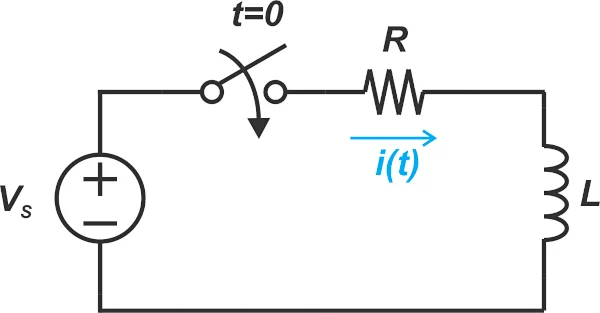
图 1. RL 电路示例。
假设输入是正弦电压,由下式给出:
\[v_s = V_{m}cos(\omega t)\]
当 t = 0 时,
开关闭合,输入施加到电路。可以证明,流经电路的电流由下式给出:
\[i=\frac{-V_{m}}{\sqrt{R^2+\omega^{2}L^{2}}}cos(\theta)e^{-(\frac{R}{L})t}+\frac{V_{m}}{\sqrt{R^2+\omega^{2}L^{2}}}cos(\omega t-\theta)\]
其中 θ 是取决于 ω、L 和 R 的参数,上述方程中的项是系统的瞬态响应。顾名思义,瞬态响应是暂时的,通常会随着时间的推移而迅速消失,可能在几毫秒内消失。如果我们让开关保持闭合足够长的时间,我们将只剩下第二项,称为系统的稳态响应。
稳态响应是与输入频率相同的正弦波。它的相位和幅度可能与输入不同,但是,它具有相同的形状和频率。虽然我们在上面研究了 RL 电路,但此特性适用于任何其他线性时不变 (L
TI) 系统,无论是复杂的
放大器还是一段
导线。如果电路元件是线性且时不变的,则其对频率为 ω 的正弦输入的稳态响应是相同频率的正弦波。其他波形(例如方波)则不是这种情况,其中电路可以改变波形形状并修改其幅度和相位。
对两个正弦分量之和的稳态响应
在上面的示例中,我们观察到电路将输入相位改变 -θ,并将输入幅度乘以系数 H,由下式给出:
\[H=\frac{1}{\sqrt{R^{2}+\omega^{2}L^{2}}}\]
这意味着,通过有 θ 和 H,我们可以确定任意频率 ω 下正弦输入的稳态响应。如果我们同时在 ω 处施加两个正弦输入会怎样1和 ω2?换句话说,电路将如何响应以下输入:
\[v_s = V_{m1}cos(\omega_{1} t) + V_{m2}cos(\omega_{2} t)\]
由于假设电路是线性的,因此叠加原理指出,总输出等于各个输入元件产生的输出之和。因此,稳态响应为:
\[i=\frac{V_{m1}}{\sqrt{R^2+\omega_{1}^{2}L^{2}}}cos(\omega_{1} t-\theta_{1}) + \frac{V_{m2}}{\sqrt{R^2+\omega_{2}^{2}L^{2}}}cos(\omega_{2} t-\theta_{2})\]
其中 θ1和 θ2是 Ω 处输入分量所经历的相移1和 ω2分别。因此,如果我们知道不同频率下正弦分量的响应,我们也可以确定对任意正弦分量之和的响应。
对任意波形的稳态响应
让我们更进一步!知道了对不同正弦输入的响应,我们能否确定对周期性非正弦波形的稳态响应?例如,如果我们输入图 2 中描述的方波,我们如何确定电路的稳态响应? 请注意,图 2 仅显示了输入波形的一个周期;换句话说,假设图中描绘的部分会随着时间的推移以周期性的方式重复自身。
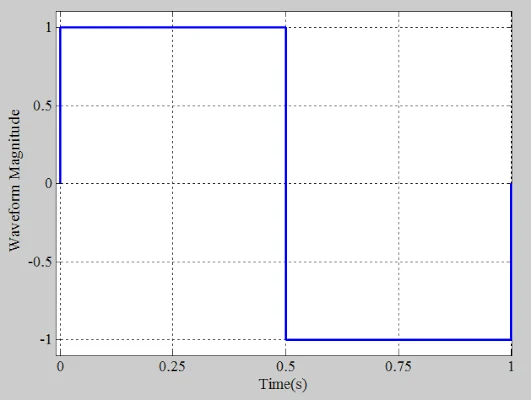
方波示例。
图 2. 方波示例。
这就是傅里叶级数的突出之处。傅里叶级数允许我们用正弦波形来描述任意周期波形,例如上面的方波。由于我们知道电路对各个正弦分量的响应,因此我们还可以应用叠加定理来找到对任意波形的响应。
正弦函数和:从正弦波和方波中学习
在讨论傅里叶级数方程之前,让我们尝试定性地描绘一些正弦函数的总和如何表示任意波形。考虑图 2 中的上述方波。我们能否用单个正弦函数来近似这个波形?
如图 3 所示,与方波频率相同(本例中为 1 Hz)的正弦波非常适合方波,并沿 x 轴表现出相同的过零点。暂时,我们不用担心这个正弦波的幅度是如何选择的。 用单个正弦波近似方波。
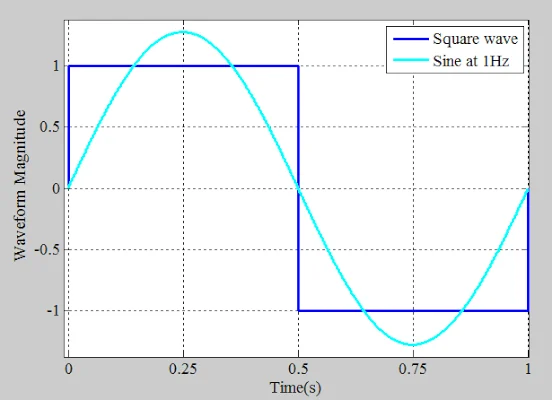
图 3.用单个正弦波近似方波。
在上图中,两个波形的整体形状有一些相似之处,但它们仍然有很大的不同。方波在每个半周期保持恒定。但是,正弦波分别在方波的正半周期和负半周期的中点达到其值和值。与正弦波不同,方波在过渡处的变化更加突然。
总体而言,正弦波似乎无法赶上方波的突然变化。在这种情况下,单个正弦波似乎不是方波的可接受近似值。但是,如果我们添加另一个正弦分量呢?通过添加另一个具有适当幅度和频率的正弦波,我们可能能够获得更好的近似值。如图 4 中的红色曲线所示,在本例中,这个新的正弦波为 3 Hz。 示例 3 Hz 的正弦波。
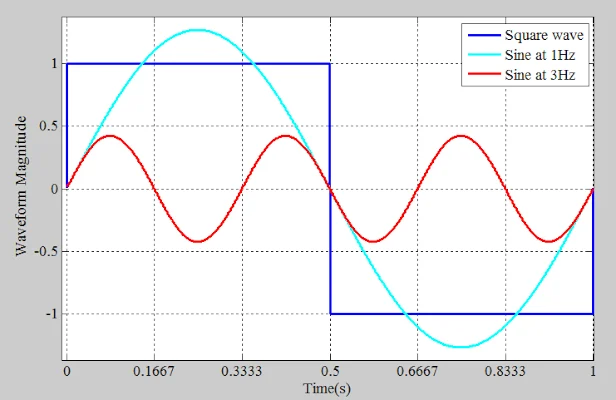
图 4. 示例 3 Hz 的正弦波。
青色和红色曲线在方波过渡附近具有相同的极性。因此,当两个正弦波相加时,会产生一个过渡比单个正弦波更尖锐的波形。然而,对于 0.1667 < t < 0.3333 和 0.6667 < t < 0.8333,两个正弦波具有相反的极性。随着更尖锐的过渡和平坦的波峰和波谷,两个正弦波的和可以产生更准确的表示(图 5)。 两个正弦波和一个方波的示例波形。
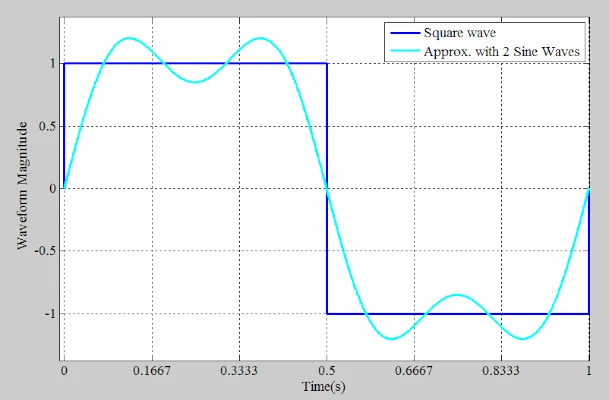
图 5. 两个正弦波和一个方波的示例波形。
这表明,通过添加更多具有适当幅度和频率的正弦分量,我们可以获得更好的方波近似。例如,使用 10 个适当选择的正弦波,我们得到图 6 所示的波形。 显示方波和 10 个正弦波的示例。
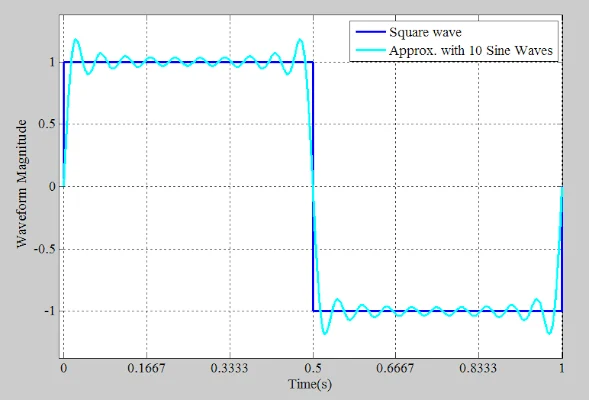
图 6. 显示方波和 10 个正弦波的示例。
既然我们知道可以将周期信号表示为正弦分量之和,剩下的问题是,如何计算给定波形的这些正弦分量?
了解傅里叶级数方程 - 求傅里叶级数表示
假设 f(t) 是周期为 T 的周期信号。我们可以用正弦分量的无限和来表示 f(t),如下所示:
\[f(t)=a_0 + \sum_{n=1}^{\infty}a_{n}cos(n\omega_{0}t)+\sum_{n=1}^{\infty}b_{n}sin(n\omega_{0}t)\]
方程 1.
哪里:
一个0一个n和 bn是信号的傅里叶系数
\(\omega_{0}=\frac{2\pi}{T}\) 表示周期信号的基频频率 \(n\omega_{0}\) 被称为波形的 n 次谐波。系数可以通过以下公式计算:
\[a_0 = \frac{1}{T}\int_{-\frac{T}{2}}^{+\frac{T}{2}}f(t)dt\]
方程 2.
\[a_n = \frac{2}{T}\int_{-\frac{T}{2}}^{+\frac{T}{2}}f(t)cos(n \omega_0 t)dt\]
方程 3.
\[b_n = \frac{2}{T}\int_{-\frac{T}{2}}^{+\frac{T}{2}}f(t)sin(n \omega_0 t)dt\]
方程 4.
请注意,积分可以在波形的任何任意周期内取,这意味着它不一定是 $$-\frac{T}{2}$$ 到 $$+\frac{T}{2}$$ 的区间。
但是,它需要是波形的一个完整周期。在某些情况下,适当地选择积分的起点可以使计算不那么麻烦。
例如,让我们找到图 7 所示的周期电压的傅里叶级数。 周期性电压示例。
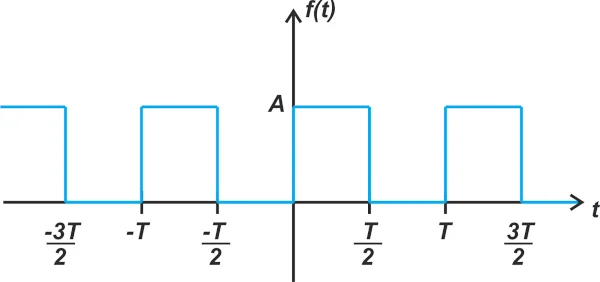
图 7. 周期性电压示例。
通过应用公式 2,我们得到:
\[a_0 = \frac{1}{T}\int_{-\frac{T}{2}}^{+\frac{T}{2}}f(t)dt=\frac{1}{T}\int_{-\frac{T}{2}}^{0}0 \times dt + \frac{1}{T}\int_{0}^{\frac{T}{2}} A \times dt=\frac{A}{2}\]
接下来,公式 3 得到 an系数为:
\[a_n = \frac{2}{T}\int_{-\frac{T}{2}}^{+\frac{T}{2}}f(t)cos(n \omega_0 t)dt=\frac{2}{T}\int_{0}^{+\frac{T}{2}}Acos(n \omega_0 t)dt = 0\]
如果你读过我本系列的另一篇文章,它是关于傅里叶系数的对称性的,上面的结果应该不足为奇。在消除图 7 中方波的 DC 值后,我们得到了一个具有奇数对称性的波形。对于奇数信号,我们有一个n= 0 表示所有 n。
,通过应用公式 4,我们得到 bn系数,如下所示:
\[b_n = \frac{2}{T}\int_{-\frac{T}{2}}^{+\frac{T}{2}}f(t)sin(n \omega_0 t)dt=\frac{2}{T}\int_{0}^{+\frac{T}{2}}Asin(n \omega_0 t)dt\]
你可以验证上述积分在偶数 n 时为零。对于 n 的奇数值,我们得到:
\[b_n = \frac{2A}{n \pi}\]
因此,将我们的结果代入公式 1,我们可以将该波形的傅里叶级数写为:
\[f(t)=\frac{A}{2} +\frac{2A}{\pi}\sum_{n=1}^{\infty}\frac{sin((2n-1)\omega_{0}t)}{2n-1}\]
请注意 n 变量是如何调整的,以考虑只有 \(\omega_{0}\) 的奇数倍的正弦曲线才是非零的。






