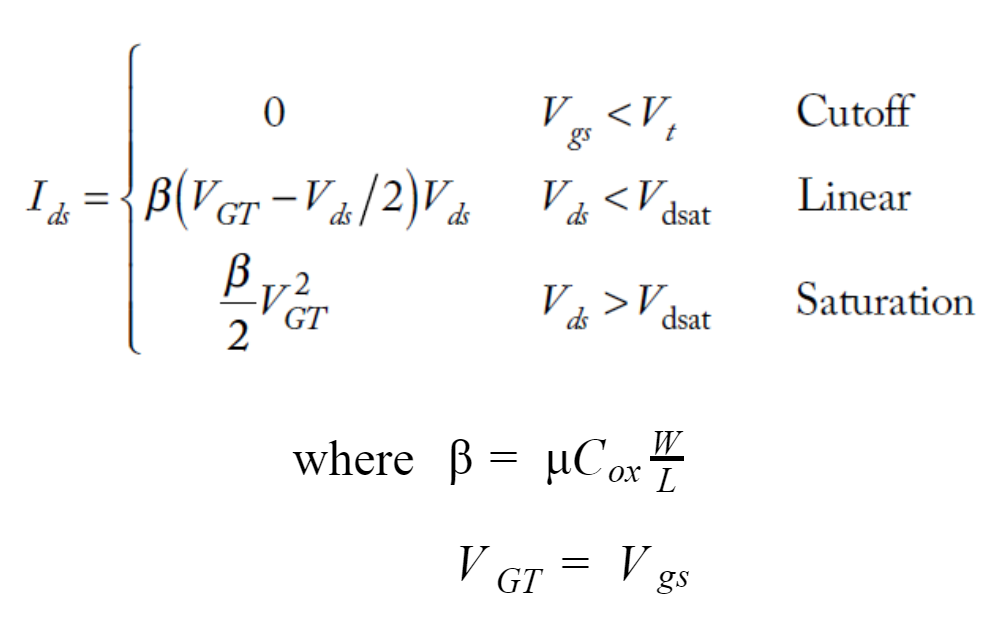摩尔定律和登纳德缩放定律描述了改进现代 IC 设计中
晶体管特征尺寸和性能的必要性;也就是说,需要每 24 个月将特定芯片中的晶体管数量增加一倍。
由于这种改进,早期晶体管电路(几毫米)与现代晶体管电路(只有几纳米)的性能、工作点和固有特性存在明显差异。
在本文中,我们将讨论理想的 MOS 晶体管分析模型以及由于 MOS 晶体管特征尺寸和设计的不断改进而产生的非理想性。此外,我们将讨论 MOS 晶体管中非理想性 (SNI) 的来源,并引入设计方法,以便在实际实施之前在模拟中正确建模 VLSI 电路。 考虑图 1 中的基本晶体管图。当没有电压施加到栅极 (g) 时,晶体管处于关闭状态。

图 1.基本晶体管工作模式
如果施加较小的栅极电压 (V gs < V t ),则该电压水平称为亚阈值电压水平,此时晶体管仍被视为关闭 (无导通)。但是,如果施加足够高的电压使其载流子 (
电子或空穴) 移动 (V gs > V t ),则会在漏极 (d) 和源极 (s) 之间创建一个通道,从而使漏极-源极电流 (I ds ) 流动。此时,晶体管处于 ON (活动) 状态。这类似于您每次打开智能手机时的状态。
在导通状态下,漏极电流 (I ds ) 随漏极电压 (V ds ) 线性增加,直至 (V ds = V gs = V dsat ),此后漏极电流保持恒定。如果漏极电压进一步增加到 (V ds > V dsat ),此时晶体管可能将产生其电流极限,因此,晶体管被称为处于饱和模式。例如,如果您继续消耗大量食物,那么根据您的身体限制,您可以做的工作量是有限的,这意味着您消耗的任何更多食物都被视为浪费。同样,晶体管也受其物理限制的限制,例如其特征尺寸(W 和 L)和掺杂水平(其所含杂质的量)。 因此,该图称为长沟道模型,栅极长度 (L) 和宽度 (W) 的晶体管的漏源电流由下式给出:
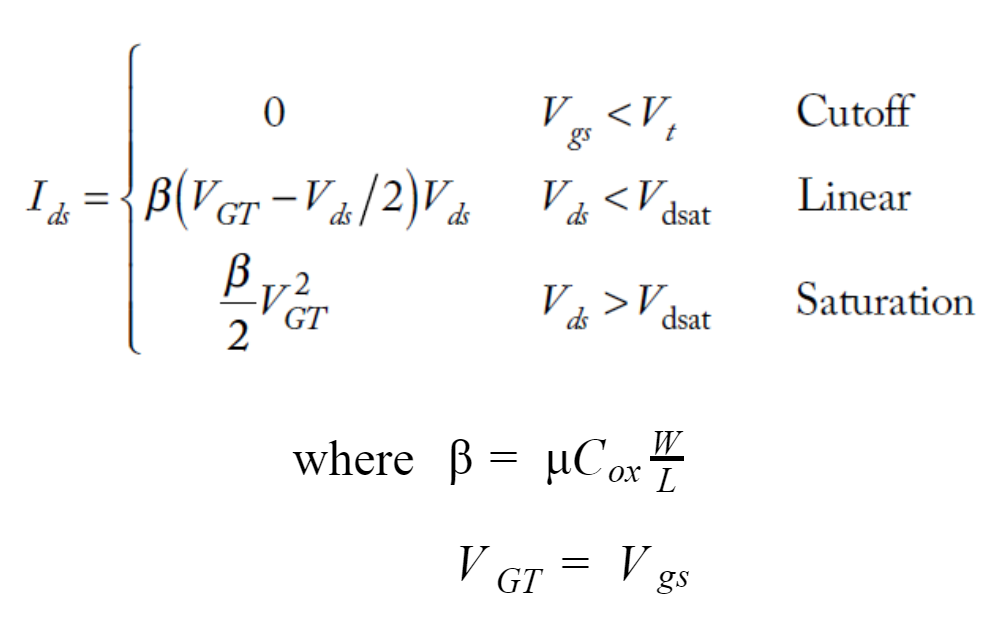
IC 设计师试图改变晶体管的 W/L 以在芯片上安装更多元件。他们越是试图将晶体管塞进芯片,就越是面临晶体管的物理限制。
因此,多年来,随着晶体管尺寸从微米技术发展到纳米技术,上述大多数假设都不能完美模拟真实晶体管的运行。例如,当晶体管处于关闭状态时,电流被假定为零,但实际上,晶体管
端子之间存在亚阈值电流泄漏,理想情况下可以忽略不计,约为纳安 (nA),但当乘以设备中的数百万亿个晶体管时,它们就很重要了。
例如,当你关闭智能手机时,你希望
电池电量保持在你离开时的水平,因此,漏电流是设计师在模拟设计时必须处理的问题。其次,据说晶体管在饱和模式下会保持其电流恒定,但在实际晶体管中,电流以较慢的速度增加,这违背了提供恒定电流的目的。
因此,在本节中,我们将讨论导致这些非理想行为的每一种机制,以及设计人员如何在其设计流程中正确地建模晶体管以进行模拟。
速度饱和和迁移率下降
速度饱和导致在高 V ds (饱和模式) 下 I ds较低。因为较高的电压会导致通道沿线的电场强度较高,从而导致载流子更频繁地发生碰撞,因此导致载流子的迁移率下降。 载体也有物理限制,因此只能保持一定的平均速度,这称为速度饱和。 (Chen, et al., 1997) 和 (Chen, Hu, Fang, Lin, & Wollesen, 1997) 给出了与此情景相匹配的通用模型,其中迁移率 (?) 被有效迁移率 ( eff ) 取代。

通道长度调制
在理想晶体管中,当晶体管处于饱和模式时, I ds与 V ds无关,从而使晶体管成为恒定电流源。但实际上,V ds(漏源电压)会在通道壁上形成耗尽层 (L d ),从而使有效通道长度小于实际通道长度,从而使有效长度 (L eff = L – L d )变为有效长度。 因此,随着 V ds 的增加,L eff会变得相对较短,从而导致横向场强降低。由于电场强度 (E) 与通道长度成正比。这种降低的场强将 I ds变化推回到线性区域,这使得 I ds随 V ds饱和而增加。

图 2. 耗尽区缩短有效通道长度
在这种情况下,可以通过将 I ds乘以依赖于早期电压 V A的因子来更好地建模, 如 (Gray、Hurst、Lewis 和 Meyer,2001) 中所述。
阈值电压 (V t ) 效应
理想情况下,阈值电压(V t)被视为恒定的,但实际上,它会随着体电压(源体电压,V sb)、漏极电压甚至沟道长度而变化。 首先,从上图 2 中的晶体管来看,当施加V sb时,它会增加晶体管导通所需的阈值电压 (V t )。考虑到这一点,V t可以重新建模为$$V_t = V_{t0} + \gamma (\sqrt[2]{?_0 + V_{sb}} - \sqrt_s)$$ 其次,沿通道产生电场的漏极电压会引起所谓的漏极诱导势垒降低 (DIBL),这会导致阈值电压降低一个因子,以 DIBL 系数表示。
$$V_t = V_{t0} - \eta V_{ds}$$
$$\eta$$ = DIBL 系数
通常,V t随沟道长度而增加,但随着 V ds的施加,沟道长度由于耗尽区的存在而减小,因此导致所谓的 V sb 滚降(减小)。
泄漏
当晶体管关闭时,假设漏源电流为零。实际上,它们会因亚阈值传导和结漏而泄漏少量电流。 对于亚阈值漏电,当 V gs < V t时,假设电流 I ds为零,但实际上,在此工作条件下电流下降得更快。当 V gs降至负值时,会形成所谓的弱反型,如图 3 所示:

图 3. IV 特性显示,当 V gs < V t时,I ds呈指数下降对于结漏电,我们观察到晶体管是扩散和衬底/阱之间的基本 PN/NP 结
二极管。当晶体管处于关断状态时,源极-栅极结二极管反向偏置。然而,反向偏置二极管仍然会传导少量电流,由经典二极管方程给出:
$$I_D = I_S ( e ^\frac{V_D}{V_T} - 1)$$
温度也是非理想性的一个重要机制,因为它主要影响迄今为止讨论的其他非理想性。例如,亚阈值漏电随温度升高而增加。阈值电压 (V t ) 也随温度降低,这使其易受 DIBL 和亚阈值传导的影响。通常,在低温下操作更合适,因为它可以显著降低速度饱和和迁移率下降。
几何依赖性
布局设计师通常会绘制具有特定通道长度(L绘制)和宽度(W绘制)的晶体管。但实际的栅极/通道长度尺寸可能会根据制造工艺而有所不同。这会导致晶体管的尺寸小于/大于预期尺寸,因此会影响阈值电压和有效通道长度以及速度饱和效应,这可能会导致一些非理想情况,如前几节所述。这种非理想情况的模型如下所示;L D 和 W D取决于制造工艺。
$$L_{eff} = L_{绘制} + X_L - 2L_D$$
$$W_{eff}= W_{drawn} + X_W - 2W_D$$