非线性的起源

　　线性性能决定了电路能够以可接受的精度处理的信号。对于较大的输入信号，电路参数会随着输入的瞬时幅度而发生显著变化。例如，考虑图 1 所示的共源放大器。

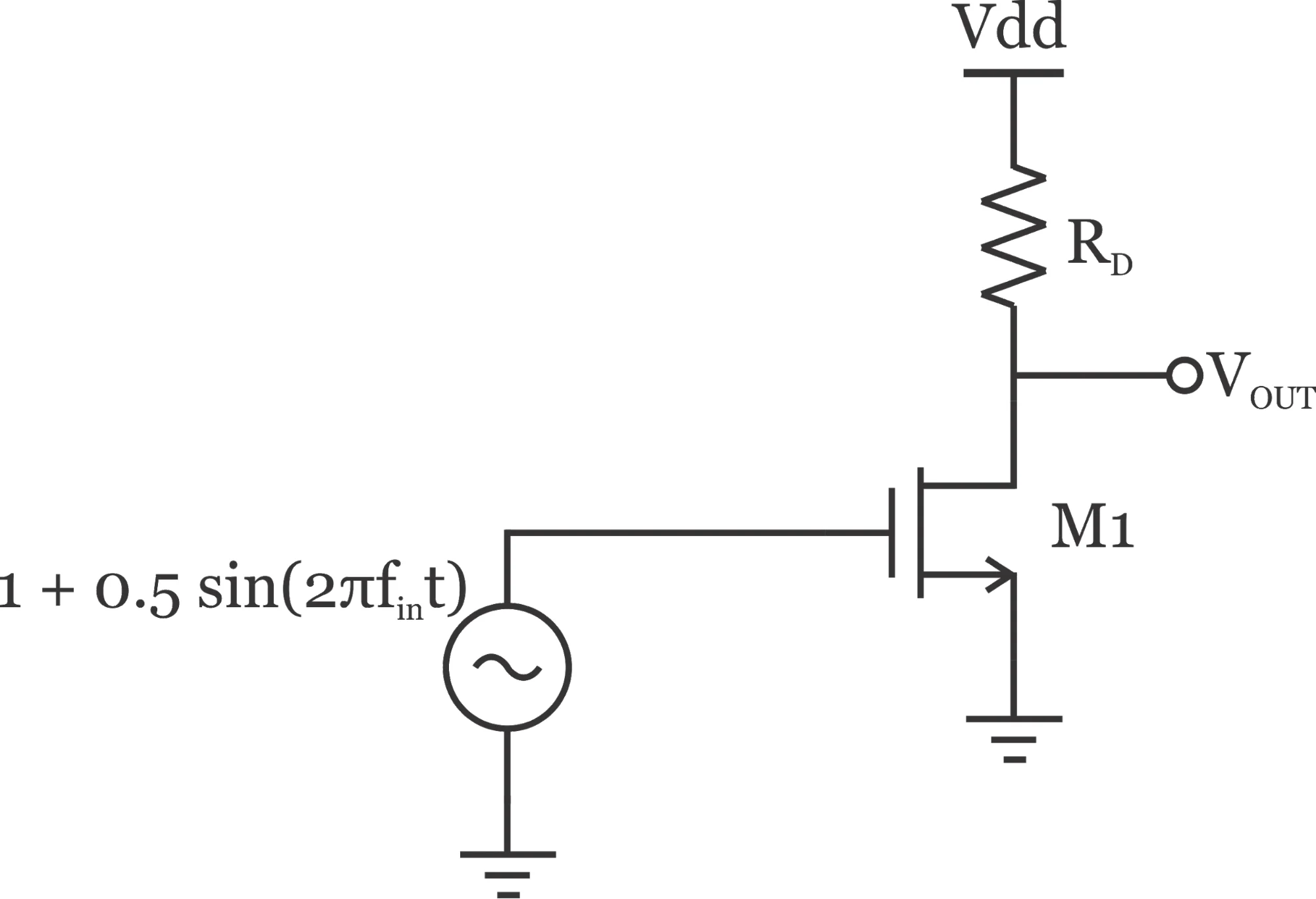
　　图 1. 共源放大器电路
　　表示晶体管跨导。考虑 MOS 晶体管的平方律模型，我们有：
　gm1=k′WL(VGS?Vth)　　其中k'是与工艺相关的参数，\frac {W}{L} \ 指定晶体管的尺寸。在这个等式中，\(V_{GS}\) 和 \(V_{th}\) 分别是晶体管栅极-源极电压和阈值电压。上面的等式表明 \(g_{m1} \) 以及增益取决于晶体管栅极-源极电压。在图 1 所示的示例中，\(V_{GS}\) 从 0.5 V 变为 1.5 V。因此，当我们接近输入峰值时，电路将表现出更高的增益。（我们假设输出不会饱和，因为晶体管漏极处存在可用的电压摆幅。如果 \(V_{GS}\) 足够大，则输出的直流值将接近地，输出的摆幅将非常有限。在这种情况下，增益实际上会随着 \(V_{GS}\) 的增加而降低）。增益随输入而变化是电路非线性的根源。请注意，随着输入幅度的增加，电路变得越来越非线性。我们在之前关于SFDR的文章中讨论过，即使输入是单音正弦波，电路非线性也会导致输出端出现几个不同的频率分量。现在，让我们看看在尝试改善电路线性度时面临的常见权衡。
　　从 0.5 V 变为 1.5 V。因此，当我们接近输入峰值时，电路将表现出更高的增益。（我们假设输出没有饱和，因为晶体管漏极处有可用的电压摆幅。如果有一个足够大的五
　输出的直流值将接近地，输出的摆动将非常有限。在这种情况下，增益实际上会随着增益随输入变化是电路非线性的根源。请注意，随着输入幅度的增加，电路变得越来越非线性。我们在上一篇文章中讨论过速度与线性度的权衡
　　线性化电路的一种常用方法是图 2 所示的负反馈技术。

　　图2.电路线性化的负反馈技术。

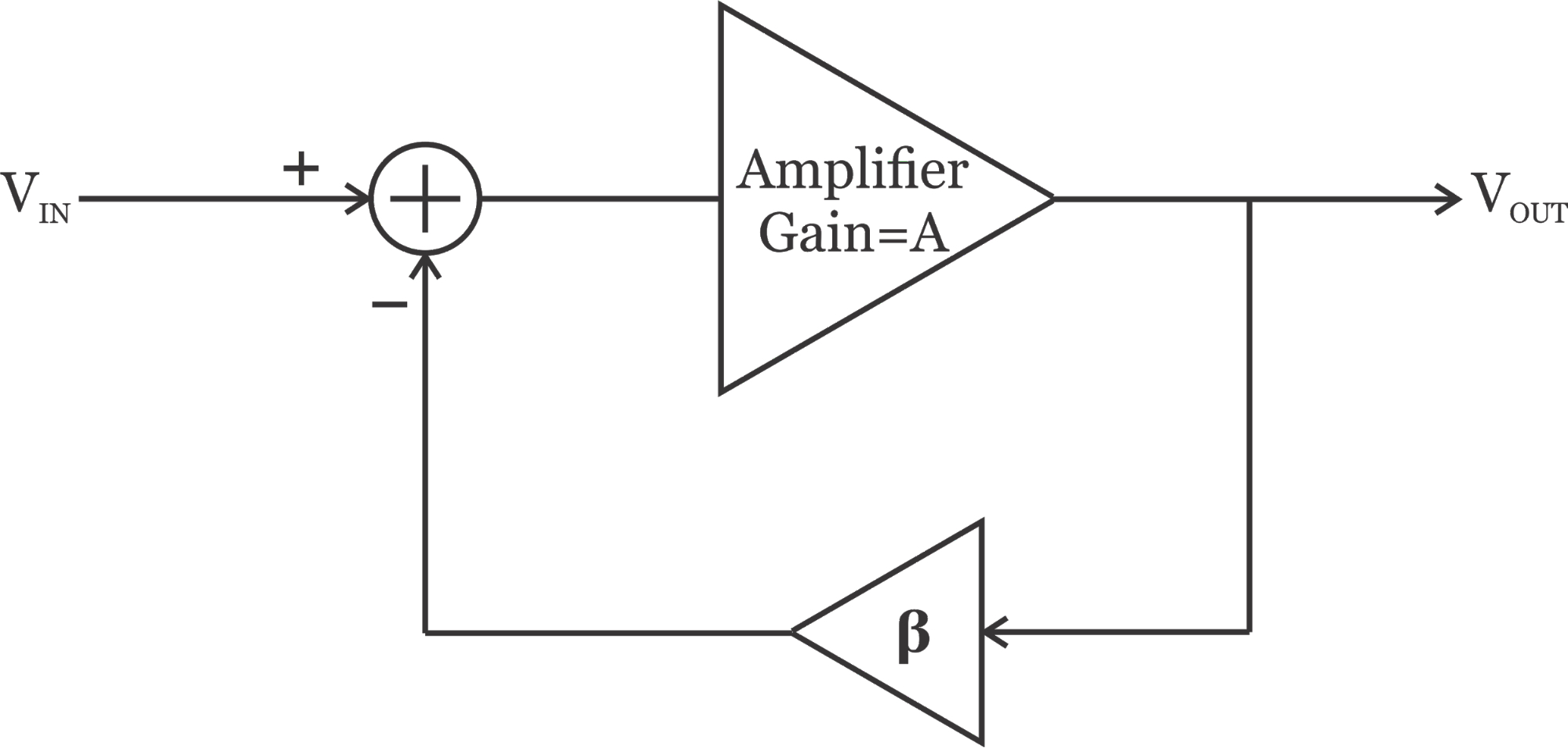
　　该电路的闭环增益由下式给出：
　　假设 \（\beta A \gg 1\），我们有
　　前馈放大器使用晶体管实现，其行为与上一节讨论的单级放大器类似，与输入相关。换句话说，A的值可以随着输入幅度而发生显著变化。但是，反馈路径 \((\beta)\) 通常使用电阻器和电容器等无源元件实现。无源元件比有源元件更具线性，我们可以假设 \(\beta\) 与输入幅度无关。如果不采用负反馈技术，增益 ( A ) 可能会随输入而变化，我们将得到一个非线性系统。但是，闭环增益 \(\left ( \frac {1}{\beta} \right )\) 是恒定的（假设 \(\beta A \gg 1\)）。
　　通常使用电阻器和电容器等无源元件来实现。无源元件比有源元件更具线性，我们可以假设β
　　与输入幅度无关。如果不采用负反馈技术。
　　这种改进的代价是什么？电路线性度通常与增益、噪声、速度和功耗相互影响。在基于反馈的线性化技术中可以观察到的一个重要权衡是速度与线性度的权衡。让我们更详细地看看这种权衡。对于开环系统，我们不必担心稳定性。系统可能会从输入到输出引入延迟，并且随着输入频率的增加，延迟也会增加。但是，引入的延迟可能不会导致严重问题。对于闭环系统则不是这种情况，我们必须仔细考虑环路延迟，因为足够大的相移可以有效地使反馈为正。通常，增加放大器的输入频率会降低其增益并增加其相移。如果输入频率足够高，环路的相移可以接近 \(180^\circ (\measuredangle \beta A=180^\circ)\)，而环路增益可能仍然大于 \(1 (\left | \beta A \right |>1)\)，从而导致不稳定。
　　为了使闭环系统稳定，我们必须应用频率补偿技术，在环路相移 \((\measuredangle \beta A)\) 为 180° 时将环路增益 \((\left | \beta A \right |)\) 充分降低至 1 以下。这在概念上相当于在环路中放置一个低通滤波器。低通滤波器抑制高频信号，因此，我们预计闭环系统的工作频率将比原始未补偿放大器的工作频率受到更多限制。总而言之，应用负反馈会提高线性度，但代价是降低工作频率。
　　增益与线性度的权衡
　　一种基本的线性化技术是源极退化。如图 3 所示，该技术在晶体管的源极处放置一个线性电阻 \((R_S)\)。请注意，我们可以将此电路视为具有“局部反馈”的结构，该结构对漏极电流进行采样并反馈与输入电压串联的比例电压。因此，源极退化会增加电路线性度也就不足为奇了。
　　在晶体管的源极处。请注意，我们可以将此电路视为具有图 3. 用作基本线性化技术的源极退化。
　　忽略晶体管的输出电阻，该电路的跨导由下式给出：
　　假设 \(g_{m1}R_S \gg 1\)，则有 \(G_{m1} \simeq \frac {1}{R_S}\)，它与输入幅度无关。这种线性度的改善是以降低增益为代价的。如果没有退化电阻 \((R_S=0)\)，我们将得到 \(g_{m1}\) 的跨导。如果我们添加退化电阻，电路将变为线性；但是，总跨导会降低到公式 2 给出的值。（请注意，该公式的分母被假设远大于 1，因此跨导会降低。）因此，增益和线性度之间可以存在权衡。
　　如果我们添加退化电阻，电路将变为线性；但是，总跨导将降低至公式 2 给出的值。（请注意，该公式的分母假定远大于 1，因此跨导会降低。）因此，增益和线性之间可以存在权衡。