了解电路稳定性

　　我们将通过一个同相放大器示例来演示电路稳定性和不稳定性的概念，如下图1（a）所示。

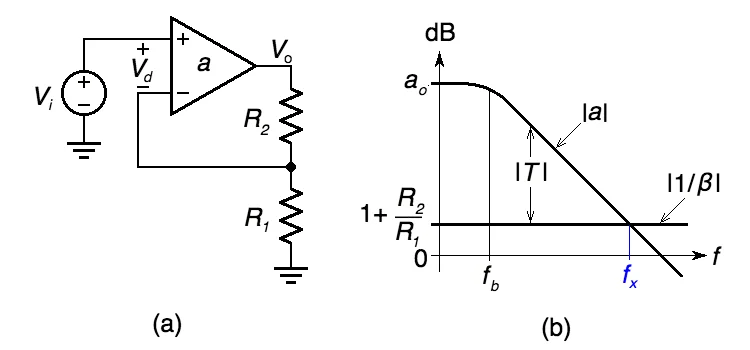
　　图 1. （a） 同相放大器和（b） 环路增益的图形可视化 |T|。
　　在本例中，同相放大器中，在放大器输入端口注入的任何信号首先被开环增益a放大，然后被反馈因子衰减
　　等式 1
　　因此，总体增益 信号在环路中经历的 T，恰当地称为环路增益，为
　　T = aβ
　　等式 2
　　改写为 T = a/（1/β），取对数，再乘以 20 转换为分贝，得到
　　|T|分贝= |一个|分贝- |1/β|分贝
　　表明我们可以可视化 |T|作为分贝图之间的差异 |一个|以及 |1/β|.图1（b）中描绘了恒定增益-带宽积运算放大器（常见的运算放大器类型）的情况。
　　频率 fx在两条曲线相交的地方，恰当地称为交叉频率，起着重要作用，因为它通过相位裕量提供了电路稳定性的定量指示 φm，定义为
　　φm= 180° + ph[T(JF公司x)]
　　等式 3
　　其中 ph[T（JF公司x）] 表示 T 在fx,
　　ph[T（JF公司x）] = pH[A(JF公司x）] + pH 值[β(JF公司x)|= p[A(JF公司x）] – pH 值[1/β(JF公司x)|
　　对于所示的单极示例，ph[1/β] = 0;ph[a] 在直流时从 0° 开始，在极点频率时下降到 –45°fb，在较高频率下渐近趋向于 –90°。通过检查，我们在这种情况下有φm? 180° – 90° = 90°。该电路的交流和瞬态响应将与普通R-C网络的交流和瞬态响应相似。
　　但是，应该φm由于某种原因而降低，那么交流响应将出现峰值φm≤ 65.5°，瞬态响应将出现振铃效应φm≤ 76.3°。为φm= 45°，电路的峰值为 2.4 dB，振铃过冲为 23%。
　　电容负载运算放大器电路

　　现在，我们将注意力转向图2所示的容性负载电路。

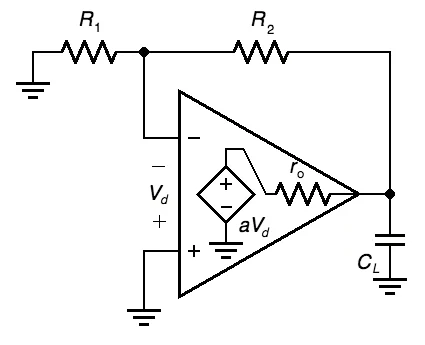
　　图2.电容负载运算放大器电路
　　该图明确显示了输出电阻ro运算放大器内部。一个设计良好的电路将具有 R1+ R型2 >> ro，因此我们可以忽略反馈网络对输出节点的加载，并说 ro和 CL建立极点频率
　　等式 4

　　我们可以从两个不同但等效的角度来研究该极点的影响，为此，我们将查看图 3 进行演示。

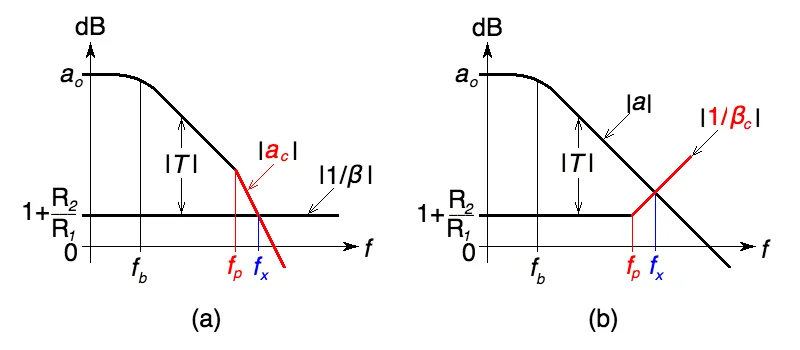
　　图3. 结合ro-CL网络 （a） 与放大器，（b） 与反馈网络。
　　在图3（a）中，我们将ro-CL网络与放大器本身有关，所以从反馈网络的角度来看R1-R2，这种组合充当具有开环增益的复合放大器
　　显然，环路增益 T 现在有两个极点频率，fb和fp，每个都有助于 ph[T(JF公司x）] 相移接近 –90°，因此电路将表现出接近零的相位裕量，通常无法容忍峰值和振铃。
　　在图3（b）中，我们将ro-CL网络与反馈网络本身结合起来，因此从放大器的相关源的角度来看，这种组合似乎具有复合反馈因子
　　请注意，当我们绘制 |1/ 时βc|， 极点频率fp成为事实上的零频率。考虑到我们现在有 ph[T(JF公司x）] = pH[A(JF公司x）] – pH[1/βc(JF公司x）]，pH[A(JF公司x）] 接近 –90° 和 pH [1/βc(JF公司x）] 接近 +90°，我们仍然有一个相位裕度接近零的系统。
　　频率补偿

　　为了使电路正常工作，我们需要修改其环路增益，以恢复可接受的相位裕量，这一过程称为频率补偿。图4中流行的方案利用了一个小的串联电阻Rs将放大器的输出引脚与CL和较小的反馈电容Cf提供从输出引脚返回到反相输入引脚的高频旁路，进行调整以中和由于以下原因导致的相位滞后。fp.

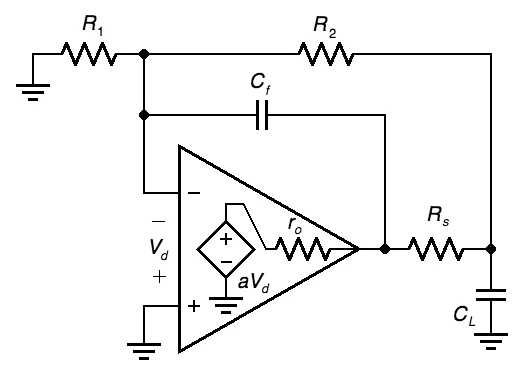
　　图4.图2所示电路的常用频率补偿方案。
　　这里的目标是使 |1/ 的上升部分向下弯曲 βc|图 2（b） 的曲线，使其看起来像 |1/β|图1（b）的曲线，我们知道它提供了大约90°的相位裕量。为此，我们需要施加两个条件：
　　高频渐近线必须等于低频渐近线，后者为 1 +R2/R1.考虑到在足够高的频率下，两个电容器都会起短路作用，很明显，R1-R2网络被禁用，因此高频渐近线变为 1 + ro/Rs（回想一下，我们假设一个设计良好的电路，负载可以忽略不计R1-R2网络）。因此，为了使渐近线相等，我们需要 1 +ro/Rs= 1 +R2/R1或
　　等式 5
　　跟Rs就位时，环内极点频率变为
　　也Cf与该组合形成高通 C-R 网络R1||R2（同样，我们假设一个设计良好的运算放大器电路，具有R1||R2 >> ro||Rs），所以它的极点频率是
　　我们祝愿Cf中和由于以下原因导致的相位滞后CL.我们通过强加 [1] 来实现这一点
　　将上述表达式替换为f1和f2并解决Cf给
　　等式 6
　　此外，闭环增益的–3 dB频率为[1]
　　等式 7
　　通过 PSpice 进行验证

　　我们希望使用图 5 的示例来验证上述注意事项，其中R2= 2R1= 20 kΩ 且CL= 100 nF。PSpice 的 741 宏模型具有ro= 50 Ω，因此我们使用等式 5 和 6（如上所示）来计算Rs= 25 Ω 和Cf= 562.5 pF。

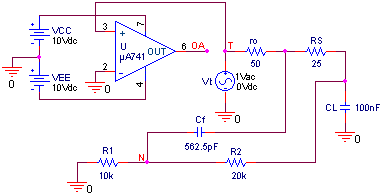
　　图5. PSpice电路，用于绘制开环增益a和1/β。

　　让我们首先检查一下补偿是否确实使 1/β 曲线变平。为了从运算放大器内部源的角度直观地看到这种情况，我们需要引入运算放大器的输出电阻 ro在外面，并对其进行测试电压Vt，如图所示。首先使用以下命令运行电路Rs= 0 和Cf= 0，我们得到图6的上升1/β曲线，该曲线在100.4 kHz时与a曲线交叉，发现ph[a]?–93.3°，ph[1/β]?+72.4°。因此，ph[T] = ph[a] – ph[1/β] = –93.3° – （+73.4°） = –165.7°，因此公式 3 给出 φm= 14.3°，这是无法忍受的峰值和振铃的原因，如图 8（下图）所示。

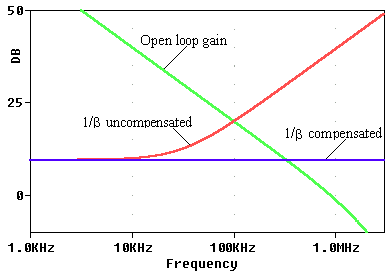
　　图6. 使用图5的电路获得的图。这里，a = V（OA）/V（T），1/β = V（T）/V（N）。

　　接下来，我们使用Rs和Cf如图所示，我们得到平坦的 1/β 曲线，该曲线在 326.2 kHz 时与 A 曲线交叉，其中 ph[T] = ph[a] – ph[1/β] = –100.7° – 0° = –100.7°，所以现在φm= 180° – 100.7° = 79.3°，这是一个更好的边距。补偿响应如图 8 所示。公式 7 预测的 –3 dB 频率为 21.2 kHz，接近 21.1 kHz 的测量值。请注意，闭环交流响应有两个极点频率：21.2 kHz 和 326.2 kHz。

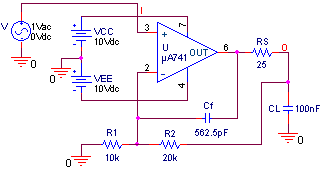
　　图7. 用于绘制闭环交流响应的 PSpice 电路。通过将输入源更改为 1.0V 步长来获得闭环瞬态响应。

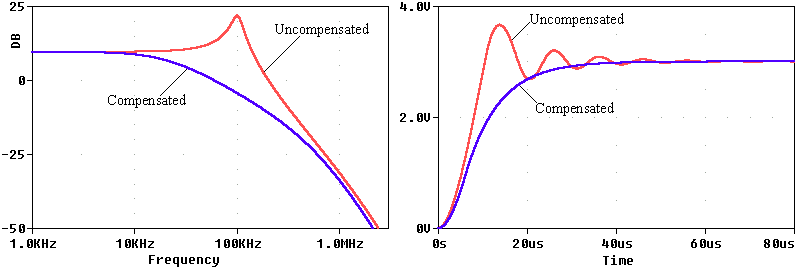
　　图8. 使用仿真电路的未补偿和补偿版本获得的闭环 （a） 交流响应和 （b） 瞬态响应。
　　结论
　　本文讨论了大容性负载会降低负反馈放大器稳定性的方式。可以通过添加电阻器和电容器来实现补偿，本文提出了一种计算这些元件的适当值的方法。
　　需要指出的是，运算放大器的输出阻抗，用下式表示ro，并不总是一个众所周知的参数;此外，在高频下，它可能会变得有反应性。因此，应将上述公式作为起点，之后设计人员可能会发现有必要调整初始值以针对手头的特定应用优化电路。