我们来看看 Sulzer 发布的带有单个调谐电阻的网络拓扑,它比传统的 RC 网络更复杂。稍后,我们将比较其模拟结果与经典网络的模拟结果。
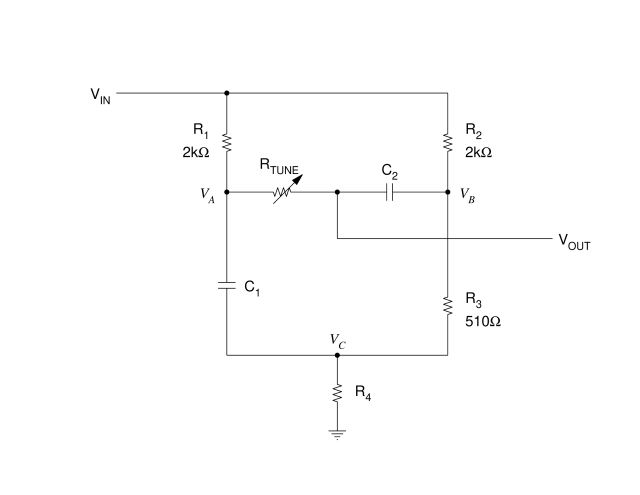
图 1 显示了一个具有一些典型组件值的示例网络。
图 1. Sulzer 的 RC
振荡器相移网络
与传统振荡器一样,反馈环路输出连接到此网络的V IN ,而 V OUT反馈到反馈增益模块输入。我们假设增益模块输入从 V OUT节点吸取的电流可忽略不计。
流入 V IN
端子的电流分成两个分压器的两条路径:
R 1和 C 1之间的分压器
R 2和 R 3之间的分压器
?两条电流路径再次汇合,总电流通过 R 4流到地。
输出电压形成于可变调谐
电阻器 R TUNE和
电容器 C 2的公共连接处。C 1和 C 2的值决定了振荡器可以调谐的频带。 现在,让我们回顾一下 Sulzer 初对其网络的概念开发,看看从 V IN到 V OUT的相移如何在某些谐振频率下通过零点。
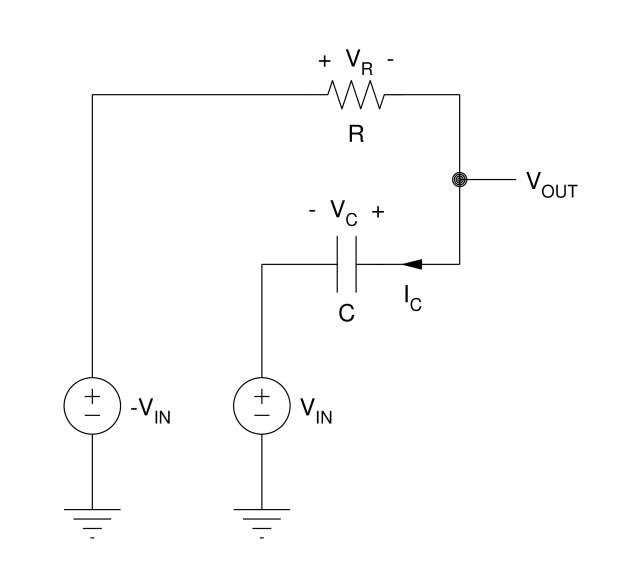
从图 2 的简单理想相移网络开始。
图 2.全通网络的理想电路
该网络由两个相位相差 180 度的正弦输入电压源 V IN 和 -V IN供电。输出电压取自电阻器和电容器的公共连接,如图所示。 这是一个众所周知的“全通”网络,其输出幅度随频率恒定且等于输入幅度,并且输出相位随着频率的升高而从 180 度连续变化到 0 度。
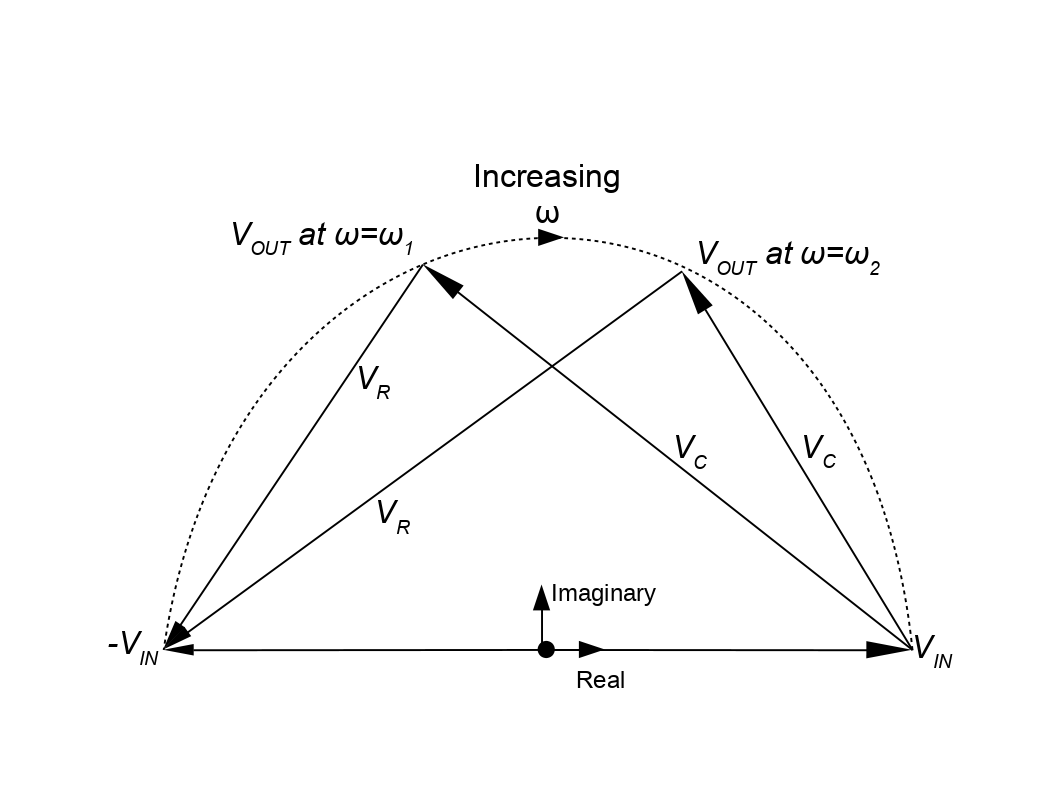
图 3 中的相量矢量图以图形方式显示了该全通网络的工作原理。
图 3.理想全通网络的相量矢量图
两个输入源的两个相量在实轴上向右和向左延伸,幅度为 V IN。由于电容器电压 V C和电阻器电压 V R的总和必须等于电路网络中两个输入源之间的总电压,因此表示 VC 和 VR 的相量的矢量和必须在图形上跨越两个输入矢量。上图中显示了两个表示V C和 V R中间点输出电压 V OUT 的相量,它们以两个不同的频率显示。
我们知道 V C和 V R之间的矢量关系。由于 VRR=IC=jωCVC
因此
VR=(jωRC)VC
。由于此关系中的 j 因子,VC 和 VR 的相量在图形上必须成直角,代表 90 度相移。随着频率的增加,VR 的长度将增加,而 VC 的长度将减少。满足这些几何约束的方法是让 V OUT的相量描绘出如图所示的半圆,因为频率会增加。这意味着输出幅度恒定等于输入幅度,相位从 180 度变为 0 度。
请注意,此相量图没有输出相位进出零度的路径,而传统网络有,因此这种类型的单个全通网络在振荡器中没有用处。Sulzer 修改了此网络,以寻找可以用单个可变电阻器进行调谐的有用电路。
我们通过将图 2 中的 -V IN源(输入电压相位偏移 180 度的副本)替换为输入电压相位偏移 -90 度的源来追踪他的设计过程。 从数学上讲,这用相量 -jV IN .表示,如图 4 的示意图和图 5 的相量图所示。

图 4.改进的全通网络的理想电路 V C和 V R的相量仍将遵循与前一个网络相同的直角关系,但 V C和 V R之和的终点将逆时针旋转至 -90 度方向,如图 5 所示。
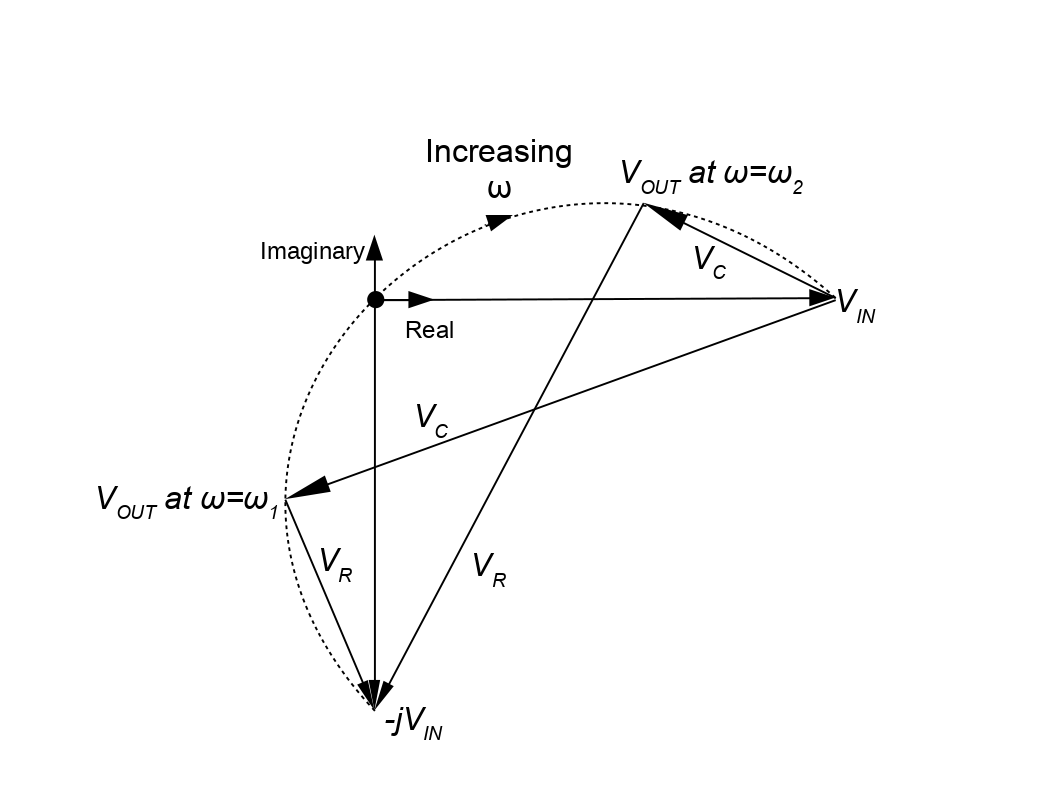
图 5.改进的全通网络的相量矢量图
随着频率的变化,这将逆时针拉伸 V OUT相量的圆形虚线路径。
从相量图到实际电路网络
因此,我们即将得到一个可用于振荡器的网络,因为现在路径经过零相移点。然而,几何学计算表明,该点将位于此相量图的原点,这意味着当相移经过零时,输出幅度也将为零。这将需要有源反馈回路来弥补无限增益,因此这显然是一种不切实际的设计。
然而,Sulzer 的设计理念是将 V IN的一小部分(没有相移)添加到 V OUT。从图形上看,这实际上会将图 5 中的整个虚线路径向右滑动,因此现在该路径将在原点右侧与实轴相交。这意味着在实际输出幅度下,将有一个频率,其中通过网络的相位为零,反馈回路可以建立持续的振荡。可以通过调节单个电阻 R 来调整与实轴相交的路径上的频率。
那么苏尔泽是如何将这个抽象的相量图转化为实际的电路网络的呢?
现代仿真工具解决旧挑战
现在,我们可以在图 1 的电路原理图中以近似形式看到图 4 中理想网络的所有组件。假设我们处于高于此分压器的低通滚降频率的频率且衰减幅度较大的情况下,R 1和 C 1分压器在 V A处形成与 V IN的 -90 度相移版本近似的版本。R 2和 R 3电阻??分压器在 V B处形成没有相移的 V IN版本,其衰减与 R 1 -C 1分压器的衰减大致匹配。R TUNE -C 2串联连接只是理想相移网络中的 R 和 C。然后,公共接地电阻 R 4会通过将电压从 VC 降至地,将大约为 V IN的一部分添加到 V OUT 。
现在,在开发这种电路拓扑时需要进行大量的近似,Sulzer 不得不在 1952 年的文章中将他的分析停留在这个相当粗糙的点上,并通过实验继续进行。(他的图形相量分析实际上包含一些错误,我在这里进行了更正。)
但通过使用现代模拟工具和一些数值优化,我们可以超越他的分析并找到电阻器 R4 的值,由于幸运的是,所有数学运算都以数值方式进行,为我们提供了一个对振荡器非常有用的网络。 例如,使用图 1 所示的元件值,优化频率传输平坦度的 R 4值终为 585 欧姆。通过在编程脚本中运行多次自动 SPICE 仿真,改变 R TUNE,并提取每次仿真中网络相移通过零点处的谐振频率,我们终得到图 6 所示的图。
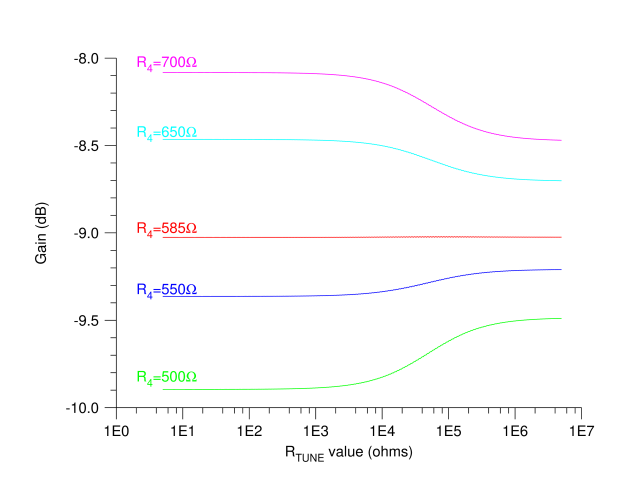
图 6.优化的 Sulzer 网络随 R TUNE值变化的模拟谐振频率和传输,其中 R 1 =2kΩ C 1 =100nF R 2 =2kΩ R 3 =510Ω C 2 =5nF R 4 =585Ω
该图显示,通过将单个电阻 R TUNE改变四个数量级,谐振频率可调整两个数量级,而传输幅度仅变化很小的几分之一 dB!使用传统 RC 网络所需的机械跟踪双调谐元件很难实现这种出色的频率幅度平坦度。对于此特性的大部分,振荡频率非常线性地跟随调谐电阻的平方根。
此时您可能会想,R 4的值要达到多么关键才能实现这种性能。 幸运的是,数学计算结果完全正确,R 4的值范围相当广泛。下一个图(图 7)显示了 R 4的五个不同值时的幅度平坦度,其中一个是值 585 欧姆,其他四个值代表较大的电阻变化。
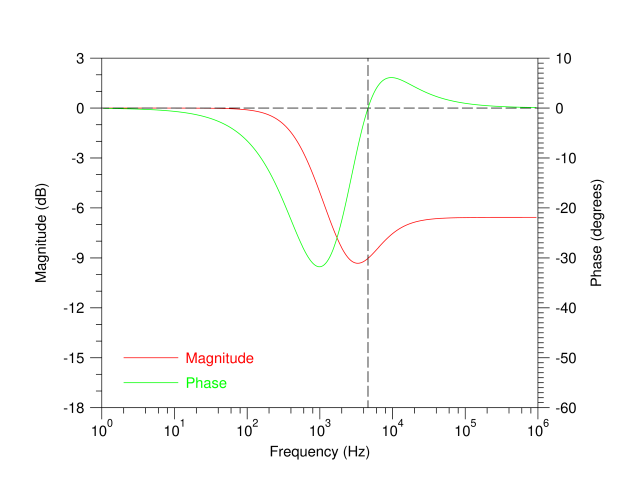
图 7.模拟了通过 Sulzer 网络传输的 R TUNE值,其中 R 1 =2kΩ C 1 =100nF R 2 =2kΩ R 3 =510Ω C 2 =5nF的五种不同 R 4值
即使远离值,传输幅度仍然平坦到小于半个dB的范围内,这个变化足够小,因此无论在整个振荡器中使用何种幅度稳定机制,例如白炽灯技术,都应该很容易将输出幅度变化降低到非常低的水平。 在 R TUNE的中心值处,例如 5kΩ,我们可以取其中一个模拟结果,并在图 8 中查看与我们之前在经典网络中看到的相同类型的增益相位图。
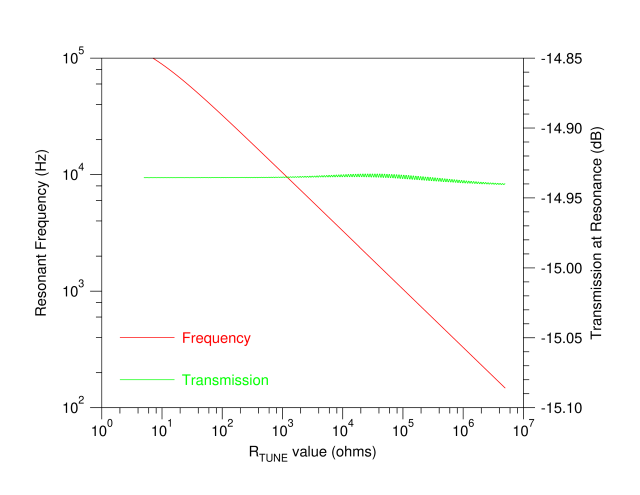
图 8.优化 Sulzer 网络的仿真结果,其中 R 1 =2kΩ C 1 =100nF R 2 =2kΩ R 3 =510Ω C 2 =5nF R 4 =585Ω R TUNE =5kΩ
在相移通过零点的振荡频率下,反馈环路增益必须弥补约 9 dB 的损失,与维恩振荡器的损失相当。此处显示的整体相位变化也与典型值为 α=4 的 Bridged-T 网络的相位变化相当。Sulzer 网络的幅度特性大致与带阻滤波器的幅度特性相同,因此在构建实际振荡器时,我们可以使用 Bridged-T 网络的反馈极性。
设计变化
图 1 的多功能网络中还可以选择其他元件值,以权衡网络衰减和总调谐范围。
例如,将 R 1和 R 2的值从 2kΩ 提高到 4.7kΩ,会降低 V A和 V B的幅度,并扩大 -90 度相移近似有效的频率范围。 现在对调整电阻值进行扫描模拟,其中 R 4的新值为 515 欧姆,可得到图 9 所示的非常宽的调整范围。

图 9.优化的宽范围 Sulzer 网络在 R TUNE值下的模拟谐振频率和传输,其中 R 1 =4.7kΩ C 1 =100nF R 2 =4.7kΩ R 3 =510Ω C 2 =5nF R 4 =515Ω
C 1 =100nF 和 C 2 =5nF的值允许从 150Hz 调谐到 100kHz 以上。更大的电容值允许在一个频带内非常线性地覆盖几乎整个音频范围,而这种振荡器正是 Sulzer 在其原始文章中所针对的。对于如此宽的频率范围(大约三个数量级),其代价是通过 Sulzer 网络的衰减增加到大约 15 dB,并且需要有源反馈
放大器的更高增益。 在 R TUNE =5kΩ的中心值处进行模拟表明,图 10 中的增益模块必须克服更深的衰减。
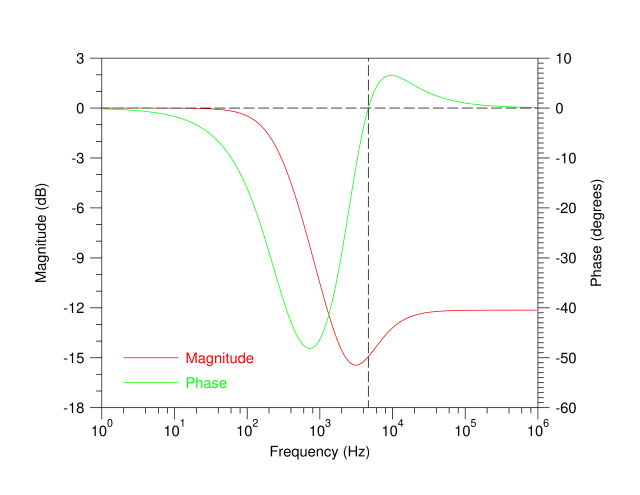
图 10.优化宽范围 Sulzer 网络的仿真结果,其中 R 1 =4.7kΩ C 1 =100nF R 2 =4.7kΩ R 3 =510Ω C 2 =5nF R 4 =515Ω R TUNE =5kΩ
这可能意味着失真会略高,因为更大的衰减会消除环路增益,从而抑制任何增益非线性。









