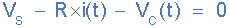下图显示一个电容器 (  C ) 与一个电阻器 ( R ) 串联，  形成一个RC 充电电路，通过机械开关连接在直流电池电源 (  Vs  ) 上。在时间零点，当开关首次闭合时，电容器通过电阻器逐渐充电，直到电阻器两端的电压达到电池的电源电压。电容器充电的方式如下所示。

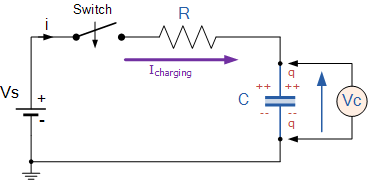
　　RC 充电电路
　　rc充电电路
　　假设上述情况，电容器C已完全“放电”，开关 (S) 已完全打开。这些是电路的初始条件，然后t = 0、i = 0和q = 0。当开关闭合时，时间从t = 0开始，电流开始通过电阻器流入电容器。

　　由于电容器两端的初始电压为零（  Vc = 0  ），在 t = 0 时，电容器似乎与外部电路短路，并且流过电路的电流仅受电阻器R的限制。然后，根据基尔霍夫电压定律 (KVL)，电路周围的电压降如下：

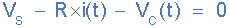
　　基尔霍夫电压定律
　　现在流经电路的电流称为充电电流，可根据欧姆定律得出：i = Vs/R。

　　RC 充电电路曲线

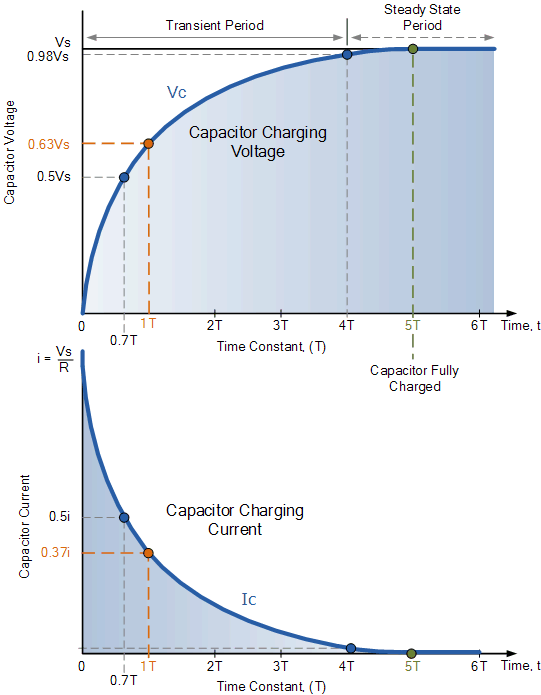
　　rc 充电电路曲线
　　电容器 (C) 以图中所示的速率充电。RC 充电曲线的上升在开始时要陡峭得多，因为充电开始时充电速度快，但随着电容器以较慢的速率吸收更多电荷，充电速度很快呈指数下降。
　　随着电容器充电，其极板上的电位差开始增加，电容器电荷达到其可能充满电电压的63%的实际时间在我们的曲线中为0.63Vs，被称为一个完整的时间常数 (  T  )。
　　这个0.63Vs电压点被缩写为1T（一个时间常数）。
　　电容器继续充电，Vs和Vc之间的电压差减小，电路电流i也减小。然后， 当电容器充满电时，其终状态大于五倍时间常数 (  5T )， t = ∞，i = 0，q = Q = CV。在无穷大处，充电电流终减小到零，电容器就像开路一样，电源电压值完全跨过电容器，因为Vc = Vs。
　　因此从数学上来说，我们可以说电容器充电至一个时间常数（  1T  ）所需的时间为：
　　RC 时间常数，Tau
　　rc时间常数公式
　　该 RC 时间常数仅指定充电率，其中R以Ω为单位，C以法拉为单位。
　　由于电压V与电容器上的电荷有关，由公式Vc = Q/C给出， 因此充电期间任何时刻电容器两端的电压 (  Vc ) 定义为：
　　电容电压
　　在哪里：
　　Vc是电容器两端的电压
　　Vs是电源电压
　　e是欧拉表示的无理数：2.7182
　　t  是自施加电源电压以来经过的时间
　　RC是RC 充电电路的时间常数
　　经过相当于 4 个时间常数 (  4T  ) 的周期后，该 RC 充电电路中的电容器几乎已充满电，因为电容器板上产生的电压现已达到其值的 98%，即0.98Vs 。电容器达到此4T点所需的时间段称为瞬态周期。
　　经过5T的时间后，电容器现在已充满电，电容器两端的电压 (  Vc  ) 大约等于电源电压 (  Vs  )。由于电容器已充满电，电路中不再有充电电流流动，因此 I C = 0。此5T时间段之后的时间段通常称为稳态期。
　　然后，我们可以在下表中显示给定时间常数的 RC 充电电路中电容器的百分比电压和电流值。
　　遥控充电台
　　时间
　　常数RC 值百分比
　　电压当前的
　　0.5 时间常数0.5T = 0.5RC39.3%60.7％
　　0.7 时间常数0.7T=0.7RC50.3%49.7％
　　1.0 时间常数1T = 1RC63.2％36.8％
　　2.0 时间常数2T=2RC86.5％13.5％
　　3.0 时间常数3T=3RC95.0％5.0％
　　4.0 时间常数4T=4RC98.2％1.8％
　　5.0 时间常数5T=5RC99.3％0.7%
　　请注意，RC 充电电路的充电曲线是指数的，而不是线性的。这意味着实际上电容器永远不会达到 100% 充满电。因此，出于所有实际目的，经过五个时间常数 (5T) 后，它会达到 99.3% 的电量，因此此时电容器被视为已充满电。
　　由于电容器两端的电压Vc随时间而变化，因此在每个时间常数（5T ）内都有一个不同的值，我们可以计算出任何给定点的电容器电压值Vc 。
　　教程示例 No1

　　计算以下电路的RC 时间常数τ 。

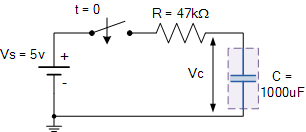
　　rc 充电电路示例时间常数τ可用公式T = R x C计算，单位为秒。
　　因此，时间常数τ为：  T = R x C = 47k x 1000uF =  47 秒a) 当时间常数恰好为 0.7 时，电容器板上的电压值是多少？
　　在 0.7 时间常数 (  0.7T  ) 时，Vc = 0.5Vs。因此，Vc = 0.5 x 5V = 2.5Vb) 在 1 个时间常数下，电容器两端的电压是多少？
　　在 1 个时间常数 (  1T  ) 时，Vc = 0.63Vs。因此，Vc = 0.63 x 5V = 3.15Vc) 从电源给电容器“完全充电”需要多长时间？
　　我们了解到，电容器将在5个时间常数（5T）后充满电。
　　1 个时间常数（  1T  ）= 47 秒（来自上文）。因此，5T = 5 x 47 = 235 秒d) 100 秒后电容器两端的电压是多少？
　　电压公式为Vc = V(1 – e (-t/RC) )，  因此变为：Vc = 5(1 – e (-100/47) )其中：V = 5 伏，t = 100 秒，RC = 47 秒（从上方开始）。
　　因此，Vc = 5(1 – e (-100/47) ) = 5(1 – e -2.1277 ) = 5(1 – 0.1191) = 4.4 伏我们在这里看到，电容器上的电荷由表达式给出：Q = CV，其中C是其固定电容值，V是施加的电压。我们还了解到，当电压首次施加到电容器的极板上时，它会以由其 RC 时间常数τ决定的速率充电，并在五个时间常数或 5T 之后被视为充满电。