原始的 468-4 无源滤波器设计
　　快速回顾一下，图 1 中的网络是在 20 世纪 50 年代开发的，用于提供阻抗为 600 Ω 的音频系统所需的频率响应。

　　适用于 600 Ω 电路的 468-4 滤波器的无源网络实现

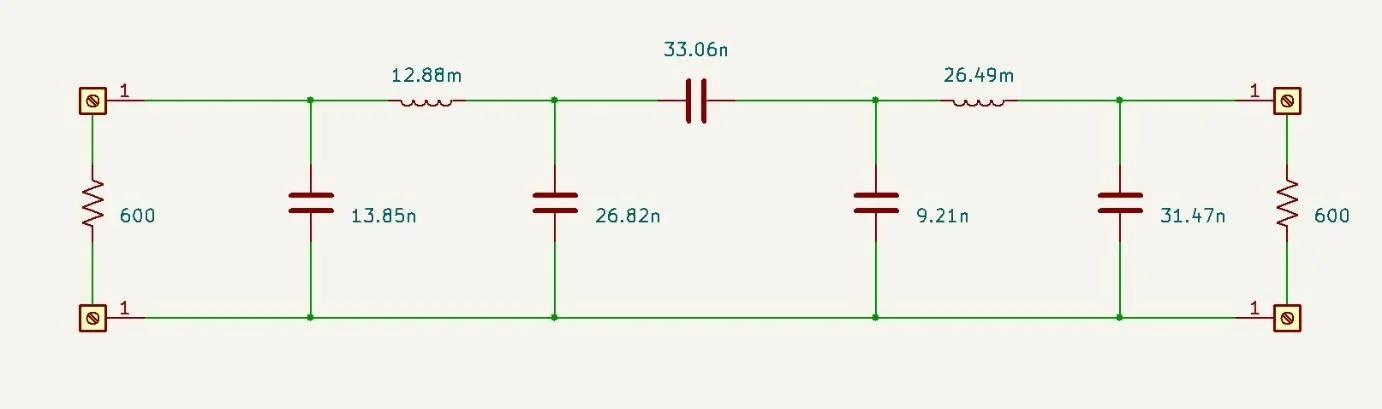
　　图 1. 468-4 滤波器用于 600 Ω 电路的无源网络实现。
　　左侧和右侧分别显示了源电阻和负载电阻，但没有信号源。此电路需要在输出端使用放大器来补偿其显著的插入损耗。
　　电感电阻的影响
　　规格的频率响应可能是通过测量原始网络来确定的，该网络受电感器损耗的影响。
　　该规范要求电感器的 Q 因数在 10 kHz 时超过 200，但由于以下两个原因，这并不是一个充分的规范：
　　电感器具有串联电阻和（如果不是空芯）并联损耗电阻，但我们不知道每个电阻的大小。
　　并联损耗与频率有关，因此不能完全通过固定电阻器来建模。
　　对电感器的调查显示，在允许电感器 Q 值为 200 的情况下，串联电阻和并联电阻之间的损耗分布对频率响应的影响很小，即使在关键的 6 kHz 至 14 kHz 范围内也是如此。对于没有电阻损耗的理想电感器也是如此。要使并联电容产生任何影响，它们必须在纳法拉范围内，当然，它们不是。
　　电容变化的影响
　　规范还指出，可能需要调整 33.06 nF 电容的值以满足频率响应的指定容差限值。我使用 LTspice 仿真研究了这些影响。将 33.06 nF 电容改变 ±5% 的影响可以忽略不计（微贝！）。
　　模拟元件变化的影响
　　在仿真中，我们可以在 ± 5% 的容差范围内改变组件。图 2 绘制了所有网络变体的频率响应，其中规格限值以黄色突出显示。

　　改变元件值对无源网络 468-4 音频噪声滤波器的频率响应影响不大

　　图 2.改变元件值对无源网络 468-4 音频噪声滤波器的频率响应影响不大。

　　如图 2 所示，频率响应不会随着组件公差而发生很大变化，并且所有变体都符合规格。
　　谨防插值
　　然而，您可能会注意到图 2 中频率响应曲线中以 11 kHz 为中心的奇怪驼峰。在上一篇文章的模拟和测量中也看到了这个驼峰。它看起来像是数据错误，但数据是正确的。
　　原因是频率响应规范中从 10 kHz 到 12.5 kHz 的步长较大，我在模拟中复制了这一步。频率步长模拟中这个 8.1 dB 的步长迫使模拟绘图工具插入数据来绘制曲线。
　　10 kHz 和 12.5 kHz 之间的线性插值在 11 kHz 处产生 4.63 dB 的响应，而所有模拟网络的响应都非常接近 5.30 dB。如果我们在模拟中添加额外的频率步骤，11 kHz 处的峰值几乎消失了，如图 3 所示。

　　添加额外的频率步骤可以减少插值并消除响应曲线中的驼峰

　　图 3.添加额外的频率步骤可减少插值并消除响应曲线中的驼峰。
　　其余的凸起和凹陷是由于频率响应规范中的舍入效应造成的。因此，将构建和测量的滤波器的结果与模拟无源网络的频率响应进行比较，这两者都具有非常小的舍入误差。
　　将被动网络转变为主动网络
　　众所周知，您可以通过将所有组件阻抗除以固定比例因子来“缩放”任何 RLC 网络。只要源阻抗和负载阻抗包含在计算中，频率响应就不会改变。

　　1968 年，伦纳德·布鲁顿 (Leonard Bruton) 证明，如果比例因子为虚数（包括j，即负 1 的平方根），布鲁顿变换过程仍然有效。如果我们包括角频率ω ，它的效果会特别好：　ω=2πF　

 　等式 1.

　　在哪里：
　　f是赫兹频率。
　　通过虚角频率缩放电感器
　　我们将所有元件除以比例因子jω。首先检查阻抗为jωL 的电感的变化。

　　杰ω大号杰ω=大号

 　　等式 2.

　　不要被术语 L 的使用所欺骗。该阻抗与频率无关，这意味着它是一个电阻值为 L 的电阻器。在我们的电路中用电阻器替换电感器将节省成本！
　　通过虚角频率缩放电阻
　　现在，让我们看看当我们将电阻除以比例因子jω时会发生什么。
　\frac{R}{j \omega} = \frac{1}{j \omega (\frac{1}{R})}
　　等式 3.
　　这将电阻变为电容值为 (1/R) 的电容器。您可能会将此值识别为我们原始电阻的电导率 G。
　　通过虚角频率缩放电容器
　　，我们将电容器的阻抗除以比例因子jω。
　　(\frac{1}{j \omega C}) \cdot (\frac{1}{jw}) = -(\frac{1}{\omega^2C})
　　等式 4.
　　这个结果看起来不太乐观。从数学上讲，这是一个实数阻抗（这里没有“j”），电压与电流同相，就像电阻一样，但它是负的并且与频率有关。
　　它可以称为频率相关负电阻 (FDNR)，或“D 元件”。这是一种为普通电阻提供能量的有源元件，因此需要电源。幸运的是，它可以由运算放大器、电阻器和电容器构成。
　　使用对偶性来变换电路原理图
　　如果我们回头参考图 1，我们会看到 C3 两端均未接地。当将其转换为 D 元件时，这将产生一个真正的问题，因为这将需要一个浮动电源。在进行 Burton 变换之前，我们可以用另一个数学技巧和电路的对偶特性来克服 C3 问题。
　　在这个“双重化”的过程中，我们可以通过进行以下更改来转换示意图。
　　电压源电流源
　　电感电容
　　电阻电导
　　串并联
　　电感和电容会改变其性质——它们储存能量的方式以及它们的阻抗随频率变化的方式。电阻和电导不会改变其性质，因此我们可以以任何一种形式看待它们而不会引入误差。
　　元件的数值不会改变，尽管结果可能包含不切实际的值（但稍后可以修复）。生成的示意图将具有相同的频率响应。
　　如果我们将对偶过程应用于图 1 中的 468-4 滤波器电路，则必须包括源电阻和负载电阻。这些电阻从 600 Ω 转换为 600 S（西门子）电导，相当于 1.667 mΩ 电阻。
　　完成 468-4 滤波器电路上的对偶转换后，将得到图 4 底部所示的新原理图。我已在图 4 顶部复制了原始电路，以便您可以更轻松地看到对偶转换。

　　图 4.原始 468-4 音频噪声滤波器（顶部）和双无源网络版本（底部）。

　　显然，由于元件值在纳亨、毫欧姆和毫法拉的量级，这是一个阻抗非常低的网络。不用担心，我们可以解决这个问题！
　　使用布鲁顿变换缩放组件值
　　现在，我们来谈谈另一个巧妙之处：使用布鲁顿变换转换组件值。我们可以引入一个新因子来将所有组件值缩放到更方便的值。
　　我们首先将 1.667 mS 源和负载电导转换为 1 nF 的合理电容大小。如前所述，布鲁顿变换使用以下公式将电阻转换为电容：
　　\frac{R}{j \omega} = \frac{1}{j \omega G} \rightarrow \frac{1}{j \omega C}
　　等式 5.
　　现在，让我们计算比例因子：
　　\text{比例因子} = \frac{C}{G} = \frac{1\text{ E-9}}{1.667\text{ E-3}} = 6.0 \text{ E-11}
　　等式 6.
　　不要担心这是一个非常高的数字；它只是一个比例因子。
　　将电阻值除以比例因子即可得到电容值（等效地，将电导值乘以比例因子）。
　　将电容值除以比例因子即可得到 D 值。
　　将电感值乘以比例因子即可得到电阻值。

　　图5是我们对所有电路元件完成布鲁顿变换后的电路。

　　布鲁顿变换后的网络，包括 D 元素
　　图 5.布鲁顿变换后的网络，包括 D 元素（点击放大）。
　　D 元件没有标准单位名称，但我们将其称为布鲁顿，并赋予其符号 Br。我们得到的 D 值以飞布鲁顿为单位，但没关系。我们可以使用合理的元件值从运算放大器、电阻器和电容器中制作它们。请注意，它们的阻抗只是具有频率相关值的负电阻，单位为欧姆。
　　负电阻的广义阻抗转换器
　　我们将使用广义阻抗转换器(GIC)创建 D 元件。关于它们如何工作的解释相当冗长且数学化（数学简单，但内容丰富）。

　　GIC原理图如图6所示。

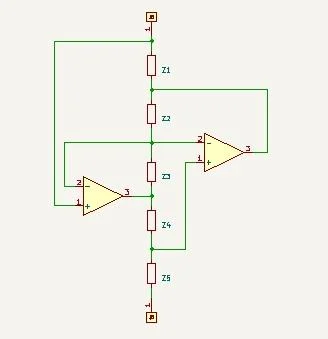
　　广义阻抗转换器示意图。
　　图6.广义阻抗转换器示意图。
　　GIC 端子之间的阻抗Z由下式给出：
　　Z = \frac{Z1 \times Z2 \times Z3}{Z2 \times Z4} 
　　等式 7.
　　我们需要一个串联链中带有两个电容器和三个电阻器的 GIC，如图 7 所示。

　　带有元件值的终 D 元件示意图

　　图 7.终 D 元件示意图及元件值。
　　我们再次为电容 C1 和 C2 选择了方便的 1 nF 值。同样，R1 和 R2 也选择 10 kΩ（另一个方便的值）。
　　必须计算 R3 值，以便为图 6 示意图中的两个 D 元件提供正确的值，使用方法如下：
　　R3_1 = \frac{D_1}{C1 \times C2} = \frac{21.47 \text{ E-15}}{1 \text{ E-9} \times 1 \text{ E-9} } = 21470 \text{ } \Omega 
　　等式 8.
　　和
　　R3_2 = \frac{D_2}{C1 \times C2} = \frac{44.15 \text{ E-15}}{1 \text{ E-9} \times 1 \text{ E-9} } = 44150 \text{ } \Omega
　　等式 9.
　　我们得到的 R3 值与 R1 和 R2 属于同一数量级。
　　使用 LTspice 模拟我们的滤波器设计
　　我们现在可以使用 LTspice 来模拟我们的滤波器，以检查它是否按预期工作。图 8 显示了 LTspice 原理图，其中我还包含了无源滤波器作为参考。

　　

　　图 8. 468-4 音频噪声滤波器的 LTspice 仿真原理图.
　　原理图显示了电阻的值，电阻可以由 E12 ±1% 容差电阻的串联或并联组合而成。我使用 TL07x 运算放大器进行此模拟。
　　据称，这种滤波器实现方式比使用传统滤波器部分的实现方式对元件值的容忍度更高。然而，这个问题太复杂了，这里不便深入讨论。
　　图9显示了模拟结果。

　　图 9.模拟响应与 468-4 音频噪声滤波器参考和指定公差的偏差。

　　显然，在 10 kHz 以内结果非常好，在 31.5 kHz 以内保持在较低的容差范围内，但确实会下降。这是由于运算放大器的带宽有限。使用更快的运算放大器（例如 NE5532）可以获得更好的结果，但这些运算放大器需要更多的电源电流。
　　关于电路稳定性的警告
　　终，我决定使用 LM4562 运算放大器进行硬件设计（如下所示）。使用速度更快的运算放大器时，由于复杂的闭环配置，其中一个 GIC 可能会变得不稳定。
　　使用任何 Spice 或类似的仿真工具时，强烈建议除了频域扫描（在 Spice 中称为 .AC）之外，还要运行时域仿真（在 Spice 中称为 .TRAN）。.AC 频率仿真无法检测到振荡。内部振荡的一个很好的指标是 .TRAN 仿真运行非常缓慢。
　　终测试：构建 468-4 音频噪声滤波器
　　关键测试是在现实世界中构建滤波器并测量其性能。图 10 显示了用作我之前的宽带电压表项目的附加组件的硬件原理图。

　　图 10.使用 LM4562 运算放大器的 468-4 音频噪声滤波器原理图。
　　本设计包含与上一个音频噪声滤波器设计中相同的增益调节电路。但是，该滤波器的增益变化范围预计较小。
　　图 11 显示了真实电路的频率响应与无源电路的模拟响应的对比。偏差刚好可以检测到，并且只有分贝的一小部分。成功了！

　　模拟被动式和测量主动式音频噪声滤波器响应

　　图 11.模拟的无源和测量的有源音频噪声滤波器响应。