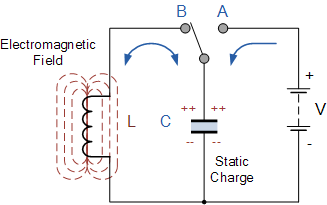
该电路由电感线圈L和电容器C组成。电容器以静电场的形式存储能量，并在其极板上产生电势（静电压），而感应线圈以电磁场的形式存储能量。将开关置于位置A即可将电容器充电至直流电源电压V。当电容器充满电时，开关切换至位置B。
　　充电的电容器现在并联连接在感应线圈上，因此电容器开始通过线圈自行放电。随着通过线圈的电流开始上升， C两端的电压开始下降。
　　这种上升的电流在线圈周围形成电磁场，从而抵抗电流的流动。当电容器C完全放电时，初存储在电容器中的能量C作为静电场现在存储在感应线圈中，L作为线圈绕组周围的电磁场。
　　由于电路中现在没有外部电压来维持线圈内的电流，因此随着电磁场开始崩溃，电流开始下降。线圈中会产生反电动势 ( e = -Ldi/dt )，从而保持电流沿原始方向流动。
　　该电流对电容器C进行充电，其极性与其原始电荷相反。C继续充电，直到电流减小到零并且线圈的电磁场完全崩溃。
　　初通过开关引入电路的能量已返回至电容器，电容器两端再次具有静电电压电势，尽管现在其极性相反。电容器现在开始再次通过线圈放电，并重复整个过程。当能量在电容器和电感器之间来回传递时，电压的极性会发生变化，从而产生交流正弦电压和电流波形。
　　这个过程形成了 LC 振荡器储能电路的基础，理论上，这种来回循环将无限期地持续下去。然而，事情并不完美，每次能量从电容器C转移到电感器L并从L转移到C时，都会发生一些能量损失，从而随着时间的推移将振荡衰减到零。
　　如果电路内没有能量损失，这种在电容器C和电感器L之间来回传递能量的振荡动作将无限期地持续下去。电能在电感器线圈的直流电阻或实际电阻、电容器的电介质以及电路的辐射中损失，因此振荡逐渐减小，直到它们完全消失并且过程停止。
　　然后，在实际的LC电路中，振荡电压的幅度在振荡的每个半周期都会减小，并终消失为零。然后，振荡被称为“阻尼”，阻尼量由电路的质量或 Q 因子决定。　　阻尼振荡

　　阻尼液晶振荡
　　振荡电压的频率取决于LC储能电路中的电感和电容值。现在我们知道，谐振电路中要发生谐振，必须存在一个频率点，其中X C的值、容抗与X L的值相同、感抗 (  X L  = X C  ) 和因此，它们将相互抵消，仅留下电路中的直流电阻来阻止电流的流动。
　　如果我们现在将电感器的感抗曲线放在电容器的容抗曲线的顶部，以便两条曲线位于相同的频率轴上，则交点将为我们提供谐振频率点（  f r或ωr  ) 如下所示。　　共振频率

　　共振频率
　　其中：f r的单位是赫兹，L的单位是亨利，C 的单位是法拉。　　那么发生这种情况的频率如下：

　　谐振频率方程
　　然后，通过简化上述方程，我们得到调谐LC电路中谐振频率f r的终方程：
　　LC 振荡器的谐振频率
　　振荡器频率方程
　　在哪里：
　　L是以亨利为单位的电感
　　C是以法拉为单位的电容
　　 r是以赫兹为单位的输出频率
　　该方程表明，如果L或C减少，频率就会增加。该输出频率通常缩写为 (  f r  )，以将其标识为“谐振频率”。
　　为了保持LC储能电路中的振荡，我们必须补充每次振荡中损失的所有能量，并将这些振荡的幅度保持在恒定水平。因此，替换的能量必须等于每个循环期间损失的能量。
　　如果替换的能量太大，则幅度将增加，直到发生电源轨削波。或者，如果替换的能量太小，随着时间的推移，振幅终会减小到零，并且振荡会停止。
　　补充这种损失能量的简单方法是从LC储能电路获取部分输出，将其放大，然后再次将其反馈回LC电路。该过程可以通过使用运算放大器、FET 或双极晶体管作为有源器件的电压放大器来实现。然而，如果反馈放大器的环路增益太小，则所需的振荡会衰减到零，如果太大，则波形会失真。
　　为了产生恒定的振荡，必须控制反馈到LC网络的能量水平。然后，当幅度试图从参考电压向上或向下变化时，必须有某种形式的自动幅度或增益控制。
　　为了保持稳定的振荡，电路的整体增益必须等于 1 或 1。如果小于，振荡将不会开始或消失为零，如果大于，则会发生振荡，但幅度将被电源轨削波，从而导致失真。考虑下面的电路。