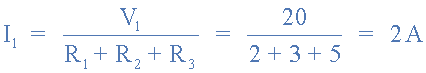叠加定理电路例二

　

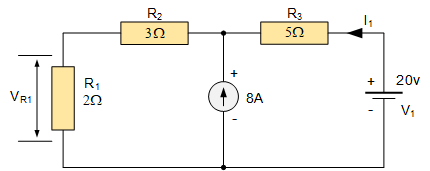
　再次，为了分析电路，我们必须短路电压源和开路电流源，以便在任何时候只留下一个电动势源为电路供电。然后首先我们将 8A 电流源开路，并使用 20V 电压源分析电路，如图所示。

　　开路电流源　　显然，我们可以看到该电路现在类似于连接在V 1上的串联电阻电路。基尔霍夫电压定律 (KVL) 给出的V 1为：I 1 (R 1 + R 2 + R 3 )，我们可以使用欧姆定律找到流过该串联电路的电流I 1 。

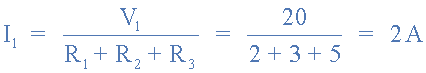
　　串联叠加电路电流
　　因此，如果串联电路周围有2安培的电流流过。电阻器R 1上的各个电压降计算如下：
　　V R1(1) = I 1 x R 1 = 2 x 2 = 4 伏
　　因此，由于 20 伏电池供电，电阻器 R 1上存在 4 伏压降。如果我们愿意，我们还可以使用分压器规则来查找环路其余部分周围的剩余压降。　　如果V 1现在短路（电压源）并且 8 安培电流源重新连接回电路。现在的电路类似于：

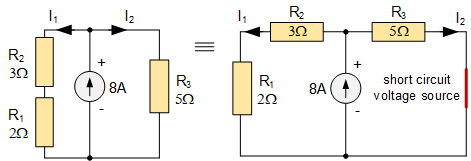
　　并联电路分流器
　　现在我们可以看到，8 安培电流源上并联了电阻，产生了通常所说的分流器电路。电流源施加到两个并联支路。个分支包含串联的电阻器R 1和R 2 ，第二个分支包含单独的电阻器R 3 。
　　基尔霍夫电流定律（KCL）告诉我们，电路中的总电流等于所有并联支路电流之和。即：I T = 8A = I 1 + I 2并且由于我们有兴趣了解电阻器R 1两端的压降，因此我们需要找到流过该并联支路的电流。　　分流器规则规定，通过一个支路的电流等于总电流乘以总电流的比率。然后通过并联支路R 1和R 2的电流计算如下：

    V R1(1) = I 1 x R 1 = 2 x 2 = 4 伏

　　并联支路电流
　　由于有 4 安培电流流过电阻器R 1和R 2的左侧并联支路，我们可以使用欧姆定律找到R 1两端的压降，如下所示。
　　V R1(2) = I 1 x R 1 = 4 x 2 = 8 伏
　　请注意，如果每个并联支路的电阻值相同（如本例所示），则电流将在每个支路之间平均分配。如果电阻值不同，则流经电阻值的支路的电流将较少，反之亦然。
　　因此，当 8A 电流源和 20V 电??压源连接回电路时，电阻器R 1两端的实际电压如下：
　　V R1 = V R1(1) + V R1(2) = 4V + 8V = 12 伏
　　同样，我们可以使用相同的分析技术来查找电阻器R 2和R 3两端的电压降。
　　叠加定理总结
　　我们在这里看到，在任何包含多个独立电压或电流源的线性电路中，我们可以使用叠加定理来找到这些独立源单独作用时产生的跨过每个电路元件的电压和/或通过每个电路元件的电流，然后将它们对电路。
　　为了使叠加定理准确地发挥作用，所有理想电压源都被短路取代，所有理想电流源都被开路取代。请注意，非理想源通常由其内部电阻代替。