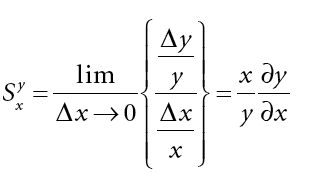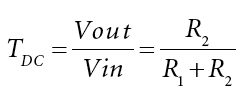电路灵敏度的定义 电路灵敏度 的一个简单但不的定义 是特定电路特性随着特定元件值的变化而变化的程度。这可以是任何电路特性:放大器增益;总线接收器输入阻抗;RF端口电压驻波比;或数字栅极阈值电压。在本文中,我们使用模拟滤波器来探索灵敏度分析,因为此信息通常对于良好的滤波器设计至关重要。我们将看到将灵敏度分析扩展到其他类型的电路是相当容易的。 公式 1 是电路灵敏度的数学定义:
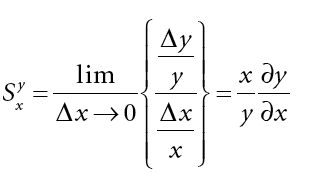
(1) 其中S 是灵敏度,X 是变化的分量,Y 是我们希望在X 变化时评估的电路特性。 这个等式的中间部分具有直观意义。它是因变量变化的百分比 Δ y / y相对于自变量变化的百分比 Δ x / x。当x的变化趋于零时取极限来 评估该比率的微小变化。 该方程非常通用,可以用来评估任何电路参数相对于任何电路元件值变化的变化。 尾注 1、2 和 3 对灵敏度进行了详细处理,并推导了我们将使用的许多方程。 简单电路示例

考虑图 1 所示的简单电路——分压器。 公式 2 是直流传递函数:
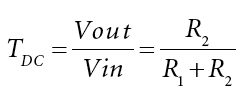
(2) 使用公式 1 计算 DC 传递函数对R 1 和R 2的灵敏度:

(3)

(4) 这些方程是什么意思?回想一下,灵敏度是因变量(在本例中为 DC 传递函数)相对于自变量( 公式 3 中的R 1和 公式 4 中的R 2 )变化的百分比。 这些灵敏度方程除了符号外都是相同的。在公式 3 中,对R 1的敏感度 为负。正如负号所暗示的,当R 1 增加时,传递函数减小。当R 2增加时,传递函数也会增加,这是预期的,因为等式 4(对R 2 的 敏感性)为正。 当R 1 远大于R 2时,方程简化为 – R 1 / R 1 = –1 且R 1 / R 1 = 1。这意味着每变化 1%,传递函数应变化近 1%在这些条件下的任一电阻器中。 以R 1 = 1000* R 2的情况为例。这里的传递函数是 1/1001 = 999e–3。如果R 2 加倍,则传输量变为 2/1002 = 1.996e–3,这是之前值的 1.998 倍,几乎翻倍。 类似地,如果R 1 加倍,传递函数将减小近两倍。将R 1 加倍会导致传递函数为 1/2001 = 0.4998e–3,这是之前值的 0.498 倍,几乎少了两倍。 另一个极端是,当R 2 远大于R 1时,导致灵敏度方程在R 1 = 0 且R 2 = ∞ 时减小至零。对于可以实现的值,敏感性将接近于零。因此,当任一电阻器变化时,传递函数变化很小。 其中R 2 = 1000* R 1,传递函数为 1000/1001 = 0.999。如果R 2 加倍,则变为 2000/2001 = 0.9995,对于元件值的 100% 变化,传递函数仅变化 0.05%。 类似地,如果我们将R 1 加倍,则传递函数变为 1000/1002 = 0.998,对于元件值的 100% 变化,传递函数仅变化 0.1%。 如果R 1 = R 2,则传递函数为 0.5,灵敏度为 –0.5 和 0.5。您预计任一电阻每变化 1%,传递函数就会变化 0.5%。让我们将R 2增加 1%。现在传递函数变为 1/2.01 = 0.4975,减少了 0.5%。同样,将R 1增加 1% 会导致传递函数为 1.01/2.01 = 5.025,即增加 0.5%。