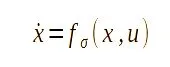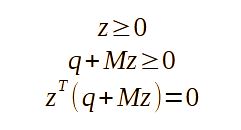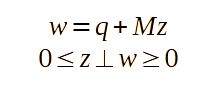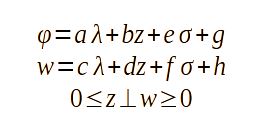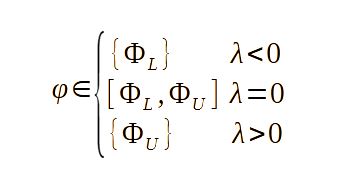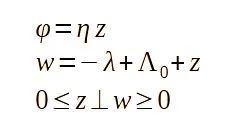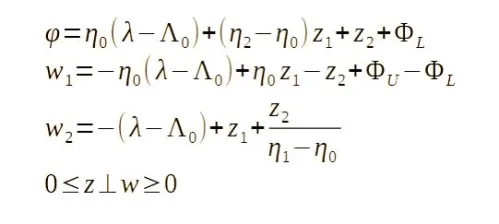切换电路在日常生活和应用科学和工程的各个领域中无处不在。电源转换器可以视为一个主要示例,因为它们几乎嵌入了几乎所有常用的设备中。即使不需要这样的系统,也可能有系统,例如汽车控制系统或更简单的弹跳球。
此外,在许多情况下,可以将两端设备的电气特性近似为零件线性(PWL)函数。这种方法也可以应用于控制开关,在该开关中,可以使用PWL特征组来描述行为。在本文中,我们提出了一种描述零件线性(PWL)函数的替代方法,特别是针对电子设备(EDS)的理想特征。
一般而言,动态系统可以根据动态方程右侧的函数的属性进行分类,也可以根据状态空间轨迹的属性进行分类。一个有趣的系统由“非平滑”动力学系统表示,其中右侧可以通过不连续导数的函数表示。
当系统的右侧可以在合适的信号中变化(让我们命名为“σ”),能够为右侧选择实际值时,它们被视为“切换”:
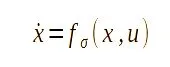
开关系统线性互补模型简介
通常,可以使用同一系统的不同表示形式。但是,每种方法都有其利弊,具体取决于分析的具体目标。例如,具有二极管的电子电路可以通过考虑二极管的“冲击利”指数特征或作为开关电路来表示为非线性平滑系统,或者通过将二极管的理想行为近似为“两态设备”(打开)(打开)或闭路),然后需要每个状态的函数f。
内部切换的存在使得难以确定模式的顺序,并且开环行为也可能具有挑战性。
已经提出了不同的数学工具来解决这些不同的问题。在下文中,我们提出了一种基于“线性互补问题”(LCP)的方法,以模型开关系统,特别是电源电路,用于外部控制的开关和状态依赖性开关。重要的是要注意,如果开关是由直接控制变量驱动的,并且如果它们是由状态依赖性条件确定的,则可以将其归类为外部。一些示例将说明该方法如何根据其静态特性来表示内部开关设备有用。
为了获得电子设备的互补表示,首先考虑如何为某些常见的PWL特性构造互补模型是有用的。
线性互补问题
作为初步步骤,我们需要引入线性互补问题(LCP)。
给定真实的向量Q和一个真实的矩阵M,线性互补问题包括找到一个真实的向量Z,以便:
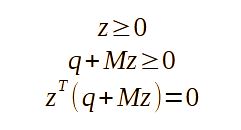
开关系统线性互补模型简介
不平等现象的位置。
定义LCP(Q,M)的条件将更紧凑,使用互补条件:
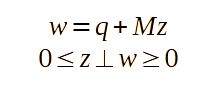
开关系统线性互补模型简介
然后?是正交性符号,即给定两个真实的向量z,w表示符号w z代表z t w = 0(标量产物为零)。正交条件意味着对于每对标量互补变量,其中至少一个必须为零。
众所周知,当M为p-matrix时,LCP(Q,M)对于任何Q都有的解决方案。如果其所有主要未成年人严格呈阳性,则矩阵M被归类为p-matrix。根据定义,每个正定矩阵都是p-matrix,尽管相反不正确。因此,如果M是正定的,则可以保证LCP(Q,M)溶液的独特性。需要解决方案的独特性,以使我们要描述的曲线具有独特的代数表示。
分段线性特征的互补表示
在许多实际情况下,近似具有分段线性函数的电子设备的真实特性(λ)很有用。通过示例,将表明,可以以以下形式写入典型的非降低PWL特征(即只有恒定或增加的段):
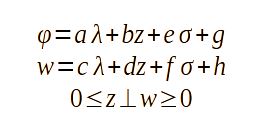
开关系统线性互补模型简介
其中z和w是互补变量的向量(因此B系数可以是矩阵),并且仅对受控的EDS仅对σ为非零,因为它代表开关控制信号(开关打开1,开关OFF为0)。
以下示例描述了功能,无论输入λ和输出的物理含义如何。
作为个示例,请考虑图1所示的步骤函数。
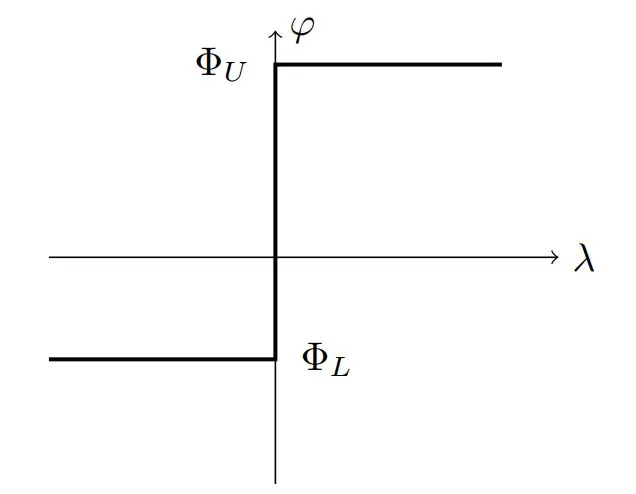
图1:“设置值”步骤功能
它被定义为“设置值”函数,因为当输入为零时,它可以假设给定集的任何值。这类函数是“经典”函数的扩展。在公式中,可以写如下:
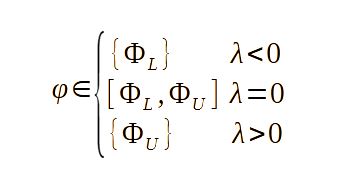
可以以互补形式表示:
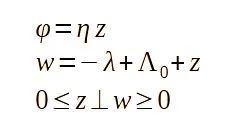
该模型可以用简单的考虑来解释。如果λ<0,则由于z 1是非负的,它将是w 2严格的阳性,并且通过使用互补约束,我们得到? =φl。如果λ> 0,则必须严格为z1,然后通过使用互补约束,它将为w1 = 0,这会导致? = z2 +φl=φU。,如果λ= 0,则方程不会对z1施加任何约束,然后对W 1的非负约束表示,意味着?可以在间隔内采用任何值[ φl ; φu ]。
步骤函数的互补模型需要两对互补变量,即(z 1 ; w 1)和(z 2 ; w 2)。原因是因为特征具有两个突破点(φL ; 0)和(φH ; 0)。
图2中的PWL函数表示二极管的理想电流特性。拥有一个断裂点可以用LCP形式表示,只有一对互补变量如下:
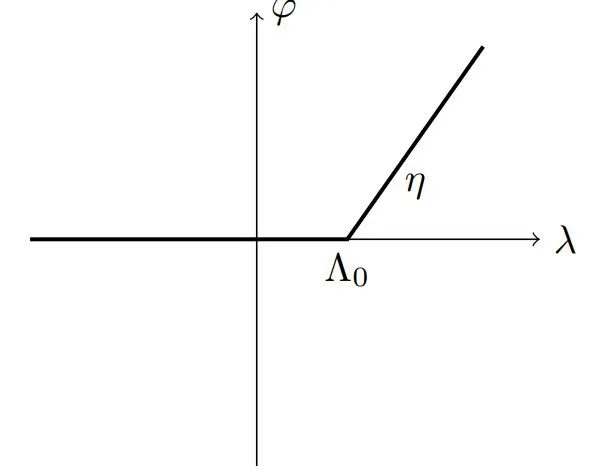
其中η是λ> λ0的特征的斜率。
图2:理想二极管的PWL特征
图3显示了具有两个突破点的非凸PWL函数。此函数可以代表许多理想化的两端设备特性:磁芯的BH曲线(或线性饱和电感),在A中的变量增益,反馈控制系统,依此类推。
互补表示形式可以如下重写:
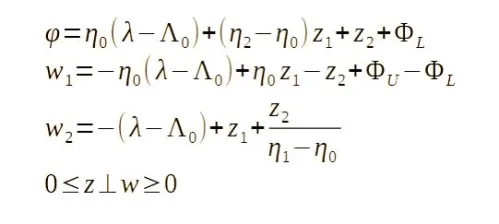
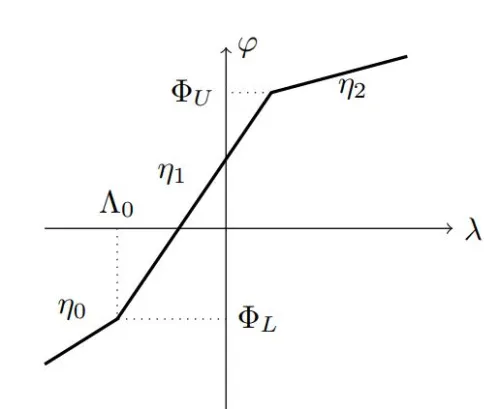
图3:非凸PWL特性的示例
通过指定方程中的参数,可以描述电路和控制理论中有趣的一些典型功能:使用η0 = η2 = 0,1/η1 = 0,λ0 = 0,我们在图1,通过为η0选择η1 = 1和零值; η2和λ0,我们获得了图4中描述的饱和函数的模型。

图4:饱和
一个示例表示典型的Zener二极管特性,如图5所示。

图5:理想的齐纳二极管特征
补充表示由:
开关系统线性互补模型简介
用λ0 < λ1。该模型可以解释如下:为W 1和W 2非负问题该问题没有解决λ<λ0和λ>λ1的解决方案,该解决方案限制了特征的定义集为λ∈[ λ0 ; λ1 ]。当λ0 < λ<λ1两个w 1和w 2都是严格的阳性,这意味着z 1 = z 2 = 0,然后? = 0;当λ=λ0时,它是w 1 = 0,并且? = -z1≤0 ;对于λ=λ1 ,它是? = z2≥0。
PWL函数的代数表示可以具有等效电路。对于具有两个以上断点的特征,使用系统的方法来确定互补表示是有用的。可以证明,任何一般的分段线性特性都可以由仅包含电阻器,独立源和理想二极管(称为RDS电路)的等效电路表示。具体而言,可以使用一对互补变量来表示理想的二极管,如图2中的特征所讨论。对于每个断点,在等效电路中需要一个理想的二极管。一旦派生了等效电路,使用Kirchhoff的定律和代数操纵即可为PWL特征制定互补表示。