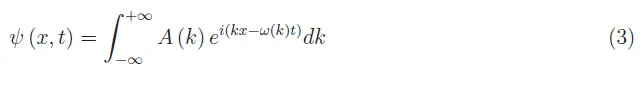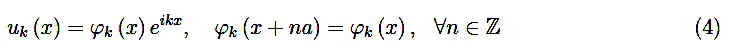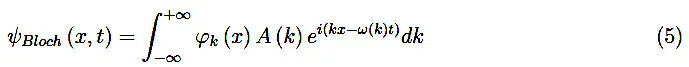在量子力学的框架中,Bloch波代表了一种“工具”,该工具使我们通过相应的特征值重建不仅表征金属,而且还表征半导体和半学分的能量带。但是,为了更大程度地遵守物理现实,我们必须考虑波数据包,即Bloch波的叠加。
为了避免计算中不必要的并发症,让我们像往常一样考虑我们的玩具模型,即一个一维晶格,其中包含周期A的周期性势能场V(x),后者是晶格的音调。在极限情况下,V(x)= 0我们有自由电子,量子力学告诉我们,能量本征函数是写入的(多达到归一化因素):

其中k是波数。在任何时候,单电子波函数都写入:

电力电子的科学笔记:电子波的群体延迟
让我们立即注意到,公式(2)描述的量子机械状态不是“局部”状态。更确切地说,由于X轴和给定的瞬间的给定点,无法定义电子定位的概率,因为正方形模块的积分延伸在整个真实轴线上。通过使用Dirac Delta函数,通过断言它是一个扩散过程来重新解释结果,即电子来自-∞,转到 +∞。从数学上讲,公式(2)中类型的对象称为不当特征(能量)。
但是,有一个数学上的技巧使我们能够对局部状态使用方程(2):足以将这些波利用在无穷大迅速消失的调制包膜中,以使上述积分融合。想到的个功能是高斯人,也是因为它在傅立叶变换下是不变的。因此,很好地表示粒子的波函数是波数据包:
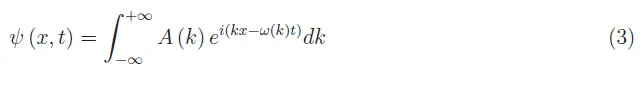
电力电子的科学笔记:电子波的群体延迟
其中a(k )是初始配置文件ψ(x, 0)的傅立叶变换;如果后者是由以x 0为中心的高斯包围的正弦振荡,则其傅立叶变换a(k)又是一个以k 0为中心的高斯,为k 0(初始剖面的正弦振荡的数量)。有关数学细节,请参见参考书目2。
在进行继续之前,我们必须了解称为分散定律的功能ω(k )的物理含义。为此,我们观察到波数据包是单色波的线性叠加。通过这种表达,我们指的是正弦振荡,该振荡具有同样的正弦定律在太空中传播的。因此,我们有两个特征数量:时间频率为频率ν和空间中的周期λ(波长)。
在真空中电磁波的情况下,这两个数量由λ= c/ν= ct连接,其中t是时间的振荡周期,C是真空中的光速。这种关系只是告诉我们,对于真空中的电磁波,波长是时间t的空间。如果我们现在叠加几个单色波或组成波数据包,我们会发现单个组件以相同的速度c传播。
从数学角度来看,以波数k =2π /λ和角频率ω = 2πν表示先前的关系很方便,获得了简单的线性关系ω(k)= ck。但是,我们看到在de Broglie波的情况下,ω(k)是二次的。因此,单个单色组件并非都以相同的速度传播。这是分散法的含义。无论如何,如果| a(k)|在波数k 0周围极高的峰值可以通过截断为一阶的泰勒序列膨胀来线性化函数ω(k)。这种情况使我们能够定义一个在k 0中计算出的ω(k)的衍生物给出的组速度v g ,该衍生物小于相速度v p = ω(k)/k。
也就是说,沿着de Broglie数据包的线路(3),我们可以编写Bloch数据包的波函数,回想起现在能量的特征函数是:
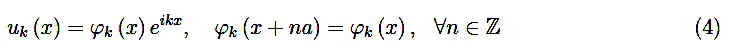
因此:
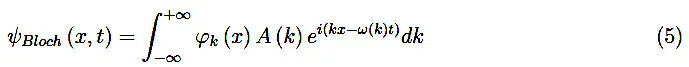
这是一个非常复杂的物体。为简单起见,我们可以参考调制包膜不取决于波数k的特定定期电势(直到降低的普朗克常数)是晶体动量。具有明显的符号含义:

因此,如果调制包膜不依赖于K,则Bloch波数据包是Broglie Wave Packet a振幅调制的DE Broglie波数据包,其周期函数的周期函数等于光栅螺距。
因此,对于上述周期电位类别,我们可以将自己限制在研究Broglie数据包的传播中,并使用以下处方:ω(k )在K中不再是Quadratic ;例如,对于玩具模型,我们找到了k的余弦函数。通常,这是正确的:物理空间中晶格的周期性转化为k空间中的周期性,使我们能够定义个布里鲁因区域或周期性的基本间隔。
因此,我们的定律比描述自由颗粒行为的简单二次依赖性要复杂得多。但是,如果ω(k)没有猛烈变化,我们仍然可以以截断为一阶的泰勒级数进行开发。这使我们能够定义一个组速度,该速度并不是能量传输发生的速度,因为在状态ψbloch (x,t )中未定义可观察到的速度(这是能量特征的叠加)。这是能量的期望值,即,在相同系统的假设集合上执行的统计平均值,该系统以组速度运输。
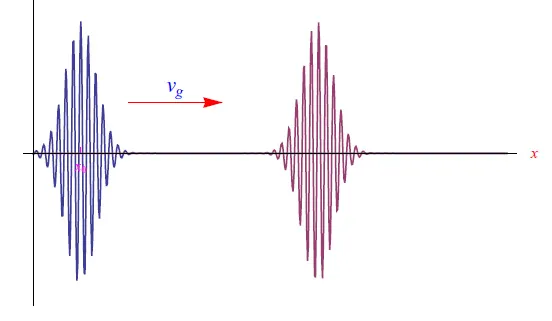
在图1和图2中,我们分别了Broglie波数据包和Bloch波数据包的传播。
让我们回忆起,只有在允许忽略ω(k)功率序列扩展中的个中的订单条款的情况下,这些结果才有效。否则,不可能定义波数据包的组速度。,让我们注意到,在描述自由粒子的情况下,发现了始终发现波函数计算的解决方案。在这里,不必串联扩展ω(k),并且可以定义组速度,因为初始剖面的傅立叶变换在给定的k 0围绕在给定的k 0上。
因此,必须在k 0中计算ω(k )的导数;确切的解决方案返回以下结果:波数据包倾向于“扩展”随时间的函数,因此我们知道粒子的腹部X的不确定性会增加。但是,不确定性存在于初的特征中,这是海森伯格不确定性原理的结果。在任何情况下,高斯数据包都具有特殊性:初始轮廓是的不确定性,因为与位置和动量有关的不确定性的产物假定值。
在进化更复杂的情况下,发生了所谓的散射,这是由于单个单色组件以不同速度传播的事实,这种现象是一种现象。
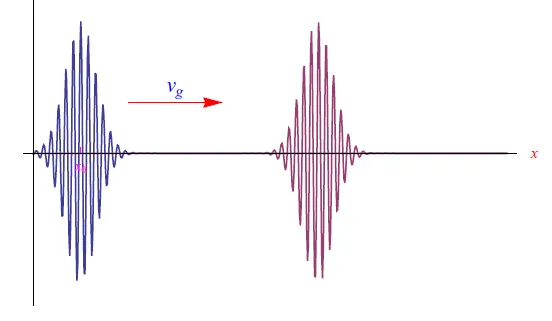
图1:带有高斯调制信封的de de de broglie波包的传播
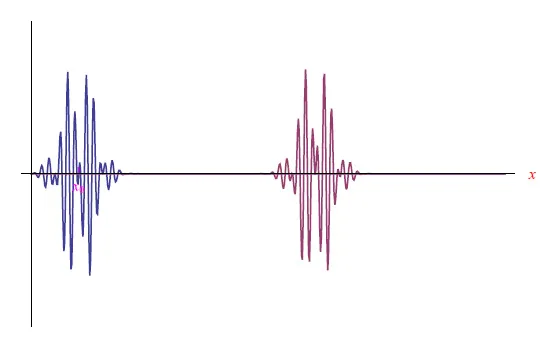
图2:Bloch波数据包的传播
耗散效应 - 群体延迟
在理解了Bloch波数据包的进化动力学之后,如De Broglie数据包(对于某些定期势能的一类周期电势)而言,它可以还原,我们可以考虑通过与晶格的相互作用确定的耗散效应。通常,为了使波浪的随之而来的衰减,波函数乘以指数阻尼因子。但是,这种选择并未现实地再现耗散动力学,因为组成数据包的所有波都会经历相同的衰减。因此,定义基于每个组件的波K数的阻尼因子。
此外,由于该阶段在量子力学(特别是单个组件之间的相对相)中起着基本作用,因此,对于更可靠的描述,定义一个复杂的阻尼系数,然后可以以极性形式表达,从而产生到极性。相位因子取决于波数k。换句话说,我们通过衰减和单个单色组件的相移来描述数据包的衰减。如果ω(k)和相对相φ(k)不会围绕主要波数K0剧烈变化,则我们可以在泰勒级数中开发这些功能,然后在阶结束时停止发展。
该过程返回一个有趣的结果:分散效应产生一个特征数量,如所见,该数量是组速度V g ,而耗散效应由特征长度λ0描述。上述效应的组合给出了一个特征时间t 0,该时间由复合函数的推导规则表示。简而言之,t 0是以ω0 = ω (k 0 )计算的φ(ω )的衍生物。波函数的分析表达是(由于它是正弦振荡的时间,我们将相位的相位放在整个积分之外,而b(k)是阻尼成分的幅度):

由此,我们看到传播被因子T0延迟,我们将其称为组延迟或过境时间。但是,没有什么可以阻止我们猜测函数φ(ω)在ω0中降低的晶格的存在,因此t0 <0。在这种情况下,t 0是一个负组延迟或同一件事,群体会提前。在光子的特殊情况下,我们了一个有趣的观察结果3:存在“带隙”光学设备,它实际上反映了狭窄频率范围的所有入射电磁辐射。即使传播高斯脉冲的质心出现在真空中的过境时间之前,也不会违反因果关系。