线性时间不变(LTI)系统无法生成除输入信号中存在的频率。由于调制将输入频率移至输出处的不同范围,因此它需要非线性,时间变化或两者兼而有之的电路。结果,许多主要从事LTI系统分析和设计的电气工程师可能不太熟悉调节器电路。 为了帮助纠正这一知识差距,本系列中的先前文章介绍了方律调节器和平衡调节器的基础知识。这两个都是基于乘数的电路。在本文中,我们将简要回顾基于乘数的调节器,然后将注意力转向切换调制器。我们将在MATLAB中模拟带通滤波器的一些指导结束讨论。 调制方法和乘数:评论 到目前为止,我们已经讨论了两种类型的振幅调制(AM): 双层限制载波(DSB-SC)调制。 常规AM。 使用DSB-SC调制,调制信号S(t)是通过将消息信号M(t)乘以正弦载波波,C(T)= A C COS(ωCT )来产生的: $$ s(t)= m(t)\ timesa_c \ cos(\ omega_c t)$$ 等式1。 传统的AM保留在传输光谱中的载波,使用以下方程式: $$ s(t)= a_c \ big(1+\ mu m(t)\ big)\ cos(\ omega_c t)$$ 等式2。 我们可以使用模拟乘数直接计算公式1和2所描述的输出信号。例如,图1说明了两种可能生成常规AM信号的配置。
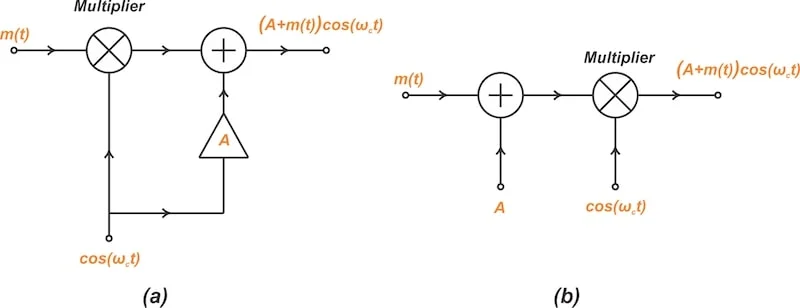
产生常规AM信号的两个可能的安排。 图1。产生常规AM波的两个可能的排列。 我们可以使用吉尔伯特细胞,霍尔效应设备或对数/防护剂放大器实现模拟乘法。但是,大多数模拟乘数以低功率水平运行,并且限于相对较低的频率。在高频下,建立具有足够大动态范围的模拟乘数远非直接。 切换调制器的关键思想 另外,我们可以使用基于开关的电路执行必要的乘法。这种类型的调制器背后的关键思想是,将消息信号m(t)乘以任何周期函数g(t),其基本频率f c在F C及其谐波时会产生AM波。如果我们假设g(t )是具有基本频率f c的均匀函数,则可以将其扩展为傅立叶级数:形式: $$ g(t)=\ sum_ {n = 0}^{n = \ infty} a_n \ cos(n \ omega_c t+\ theta_n)$$ 等式3。 将消息信号乘以g(t),我们有: $ m(t)\ timesg(t)=\ sum_ {n = 0}^{n = \ infty} a_n m(t)\ cos(n \ omega_c t+\ theta_n)$ $ 等式4。 公式4中的信号是以C,2C,3C等为中心的AM波的叠加。此方程表明,我们可以通过将消息信号乘以任何定期函数g(t)来生成AM波。频率f c。因此,将m(t)乘以纯正弦波来产生AM波并不是必需的。取而代之的是,我们可以选择更合适的函数g(t),使电路实现更加容易。 有趣的是,如果g(t)是在零和一个之间交替交替的方波,则它是一个门控函数,可以定期打开输入。在这种情况下,我们可以将乘法简化为开关操作。图2显示了如何通过单个开关来实现此门控函数。
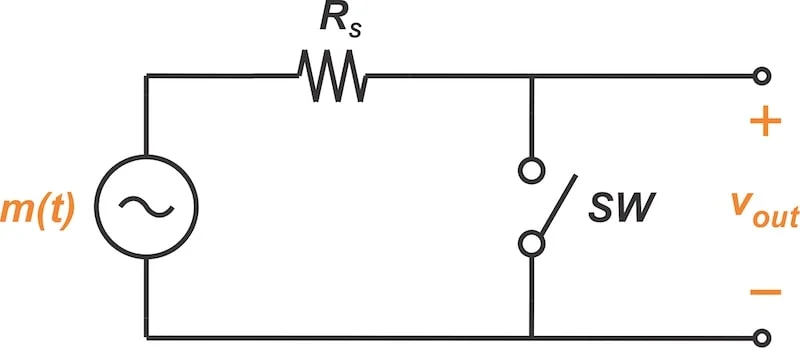
单个开关可用于将输入乘以方波。 图2。可以使用单个开关将输入乘以方波。 在上述电路中,R S模拟源电阻。开关打开时,输入将传递到输出。关闭开关时,输出降至零。因此,消息信号乘以零和一个方之间的方波切换(图3)。 开关调制器中使用的门控函数。
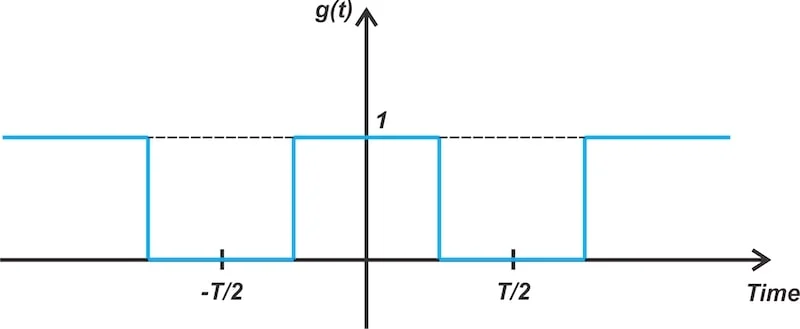
图3。上面的开关调制器中使用的门控函数。 我们将在本文稍后更深入地讨论该想法的实施。但是,在此之前,让我们检查电路的典型时间域波形。 开关调节器的时间域波形 为了检查时间域行为,我们在电路上应用单色调正弦消息。图4显示了m(t )乘以(底部)的消息信号(顶部)以及波形。 单色输入应用于调制器(顶部)和消息有效乘以的波形(底部)。
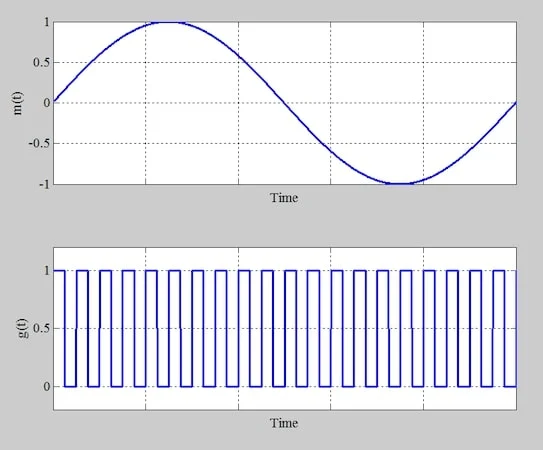
图4。应用于调制器(顶部)的单色输入和消息有效乘以(底部)的波形。 通过将这些波形倍增,我们获得了图5中的输出电压。 开关调制器生成的输出电压波形。
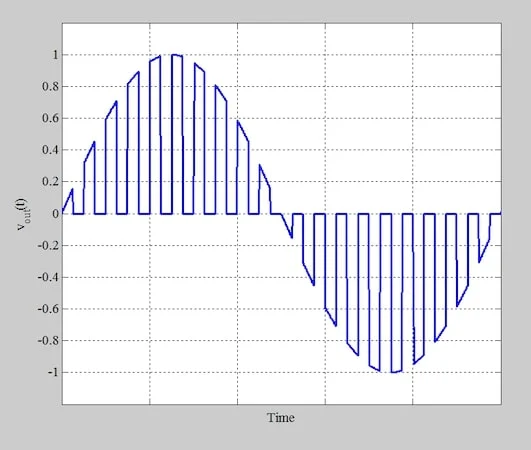
图5。调制器生成的输出波形( V OUT )。 如预期的那样,输出电压在每个周期的一半中匹配消息信号,在另一半期间下降到零。 尽管该波形的幅度类似于消息信号,但它不是典型的振幅调节信号。为了产生所需的AM信号,我们通过调谐到载波频率的带通滤波器将V传递出来。这在图6中说明了。 在施加门控函数(蓝色)和带通滤波器输出(绿色)处的信号后的信号。
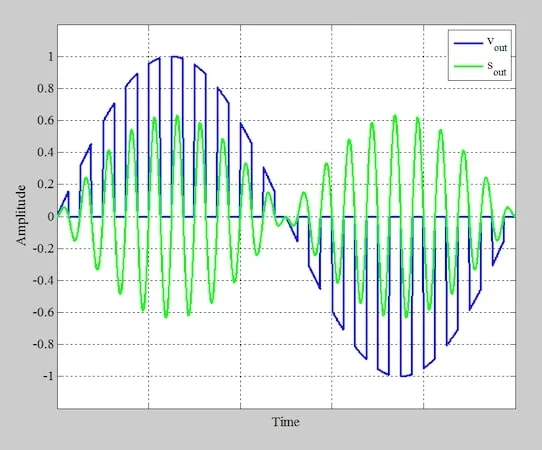
图6。在带通滤波器输出(绿色)处应用门控函数(蓝色)和所得信号后的信号。 我将在文章末尾提供代码摘录,以帮助您在MATLAB中进行必要的过滤。 电路实施:二极管桥调节器
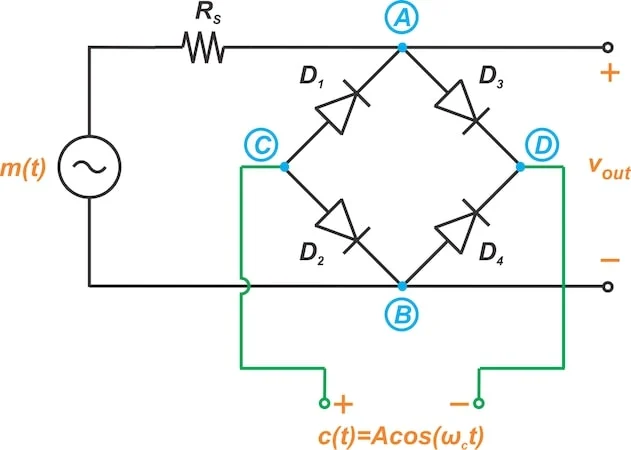
图7显示了我们如何使用二极管桥实现调制器的交换函数。 二极管桥可用于构建开关调制器。 图7。可以使用二极管桥来构建开关调节器。 当c(t)是一个较大的正值时,所有四个二极管都会进行。随着二极管D 1和D 2的匹配,二极管D 3和D 4 同样匹配,节点A和B具有相同的潜力。结果,当c(t)是正值时,节点A和B合在一起。当C(t)为负时,所有四个二极管均为开环,模仿节点A和B之间的开关开关。 开关频率取决于二极管可以打开和关闭的速度。 得出二极管桥调节器的输出信号方程 通过假设g(t)是一个方波,在零和一个之间切换,我们可以使用傅立叶级数表示来扩展其余弦函数: $ g(t)=\ frac {1} {2}+\ \ \ \ \ \ \ \ frac {2} {\ pi} \ cos(\ omega_c t)-\ frac {2} {2} {3 \ pi} { cos(3 \ omega_c t)+\ frac {2} {5 \ pi} \ cos(5 \ omega_c t) 等式5。 因此,输出电压为: $$ v_ {out}=\ frac {1} {2} m(t)+\ frac {2} {\ pi} {\ pi} m(t)\ cos(\ omega_c t)- \ frac { 2} {3 \ pi} m(t)\ cos(3 \ omega_c t) $ 等式6。 输出频谱包括以0,± F C,±3 F C,±5 F C等为中心的消息频谱的复制品。一个)。 基带消息信号(a)的频谱和调制器(b)产生的信号。
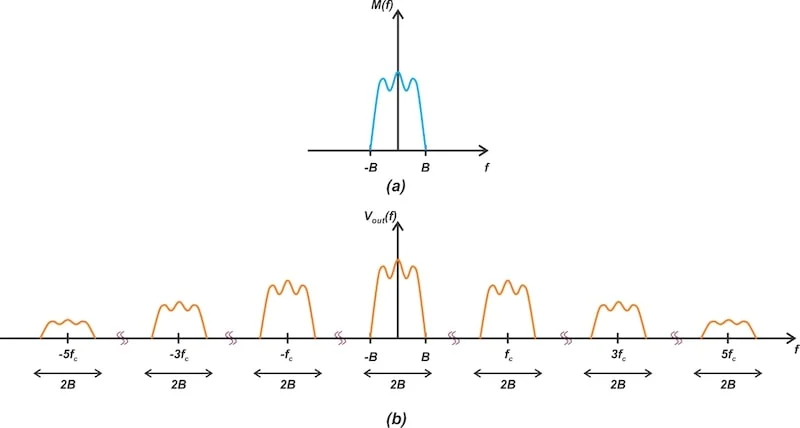
图8。基带消息信号(a)的频谱和调制器(b)产生的信号。 图8(b)中的输出频谱包括我们不想要的几个信号,以及我们所做的信号。在达到终输出方程式之前,我们需要过滤不需要的信号组件。 过滤以隔离AM信号 为了将以F C为中心的所需频谱与其他光谱组件分开,我们应该有: $$ f_c-B \ geq b \ quad \ rightarrow \ quad f_c \ geq2b $$ 等式7。 其中B是基带信号的带宽。因此,我们需要将输出信号通过带宽2 B的带通滤波器,以F C为中心,以分离所需的组件(图9)。 带有带通滤波器的二极管桥调制器的示意图。
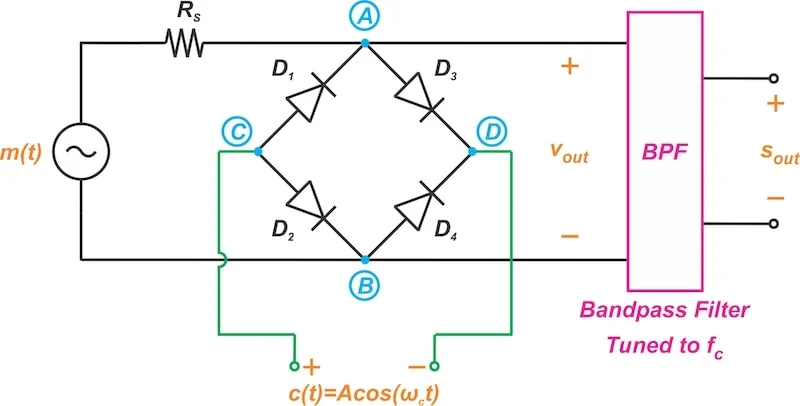
图9。带带通滤波器的二极管桥调节器的示意图。 使用理想的带通滤波器,只有以F C为中心的频谱组件通过输出,导致: $$ s(t)=\ frac {2} {\ pi} m(t)\ cos(\ omega_c t)$$ 等式8。 让我们使用图6中所示的波形来验证该方程。图中所示的调制信号是为单色调的,振幅为1的。 | m(t)| ≤1,等式8预测调制信号的值约为2/π≈0.64。这与图6中的绿色波形非常吻合,该图6的值约为0.63。








