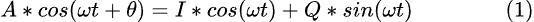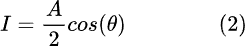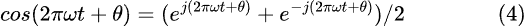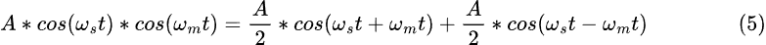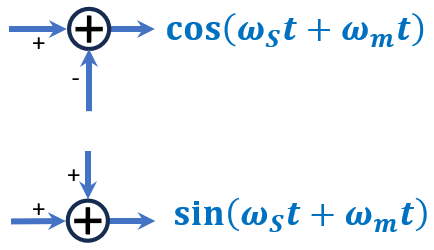I/Q 和正交概念
什么是 I/Q 数据? “I”是同相的缩写,“Q”是正交的缩写。这是组听起来神秘且容易让人望而却步的 SDR 术语,我们将其称为 I 和 Q。简单地说,如果您有一个波形,就像在示波器上看到的那样,您可以将其分解为两个正弦分量 - 一个一个基于正弦,另一个基于余弦。这是通过使用三角函数“角和恒等式”来完成的。 I 和 Q 是这些分量的幅度,因此我们的信号现在表示为:
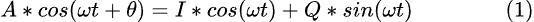
其中:“A”是原始信号幅度,并且:
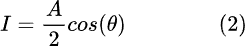

我们刚刚创建了同相信号I*cos(ωt)和正交信号Q*sin(ωt)。只是为了增加混乱,当我们一起处理同相和正交信号时,它被称为“正交信号”……叹息。
[注:在SDR项目中,IQ数据(或I/Q数据)通常是指每个采样间隔的数字数据对。]
旁白:
大多数信号处理教科书都使用指数来描述和操纵信号。例如,传输的信号始终是“真实的”,通常显示为:
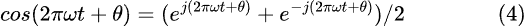
这是另一个造成混淆的公式,让刚开始接触信号处理和 SDR 的人望而却步。我会说指数表示法可以创建更清晰的数学操作,但我更喜欢使用三角表示,因为当我操作方程时,我可以在脑海中看到信号。此外,当使用每个人在高中学到的东西时,向不熟悉信号处理的人解释你的设计会容易得多。请注意,尽管大多数 SDR 仿真工具(例如 MATLAB)使用指数进行信号处理工作,但当涉及到在 MCU 中编写 C 代码时,通常会使用三角函数表示。
不用深究,这种指数表示是基于欧拉公式,它与优美且巧妙推导的欧拉方程有关。
现在,您可能想知道为什么我们要费尽心思将数据转换为这种正交形式,以及这种形式的信号有什么用处。例如,在接收器中,自无线电早期以来,仅使用输入信号并将其与另一个频率混合并提取数据就已经有效。为了回答这个问题,让我们看几个例子。
求积形式的优点示例
首先,在对输入信号进行简单混合时,您会得到两个信号作为输出:输入信号和混合频率的总和,以及这两个频率的差值。以下等式通过使用三角乘积恒等式证明了这一点:
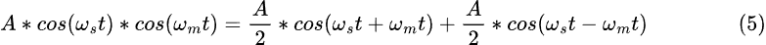
要继续在接收器中使用,您通常需要滤除其中之一,通常是较高频率。 (不需要的合成频率通常称为镜像频率,由镜像滤波器去除。)在数字接收器中,该滤波器可能会占用一些宝贵的资源(周期和内存)。使用上面的 I/Q 形式,可以创建一个混合,该混合可以仅删除总和或仅删除差值而不进行过滤。
您可以在图 1中看到其工作原理。首先,以 I/Q 格式定义混合信号:
混合信号 I 部分 = cos(ω m t)
混合信号 Q 部分 = sin(ω m t)
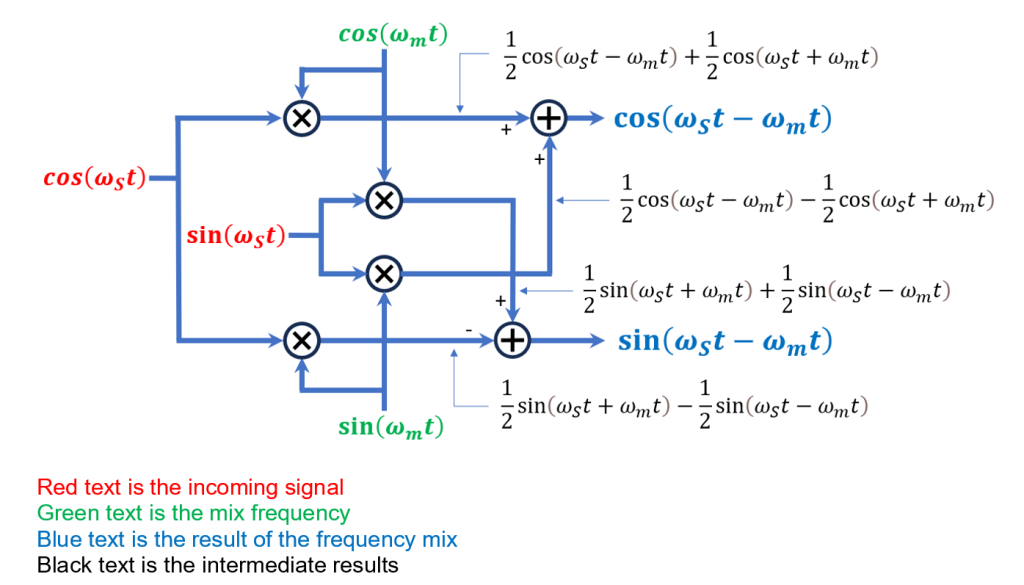
图 1正交(复数到复数)混频返回较低频率。
您可以看到混频器仅输出较低频率。如果您想要更高的频率并删除更低的频率,只需更改终添加中减号的位置,如图2所示。
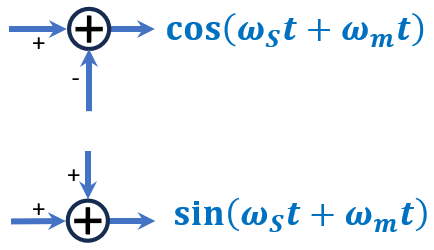
图 2返回较高频率的正交混频。
这种正交或复杂到复杂的混合是 SDR 设计中非常强大的技术。
接下来,让我们看看 I/Q 数据如何允许我们使用负频率。
当您执行经典(非正交)混合时,您获得的任何结果都不能低于零频率。结果将是两个新频率:输入频率之和以及差值的。该意味着输出频率不能变为负值。在正交混频器中,频率不受函数的约束,并且可以获得负频率。
让我们考虑一下,如果您正在扫描其中一个输入,这意味着什么。在经典混频器中,当两个输入频率彼此接近时,差频将接近 0 Hz,然后频率开始回升。在正交混频器中,差频将直接经过 0 Hz,并继续变得越来越负。
这意味着,在您正在使用的采样系统中,带宽是采样率除以 2。当使用正交表示时,您的工作带宽是两倍。当您的系统想要处理大范围的频率时,这尤其方便。您可以将任何频率移至基带;较高频率将保持在正频率中的相对位置;较低频率将保持在负频率中的相对位置。您可以通过混合上下滑动,无需图像过滤器或用图像破坏光谱。 SDR 设计中的另一种非常强大的技术。