定义谐波 在电力系统中,谐波可以定义为电流或电压在基波电压频率下的倍数。只要您观察到一个波形,并且它偏离了预期的正弦波形状,它就包含谐波。
谐波的原因 线性或非线性 AC 信号根据系统如何从
电源获取电力进行分类。谐波是由非线性系统引起的,这些系统以短而突然的脉冲消耗电流。绘制的脉冲通过引起失真来破坏电流的波形。失真会产生谐波,从而导致电源问题,从而影响负载和配电系统。非线性负载系统的示例包括电视等
电子设备。
基波电谐波 这是发电机的动力来源。它的频率称为基频或一阶谐波频率。它的值是 50 Hz 或 60 Hz,具体取决于您所在国家/地区的选择。所有电气和电子系统都在此频率下工作良好。
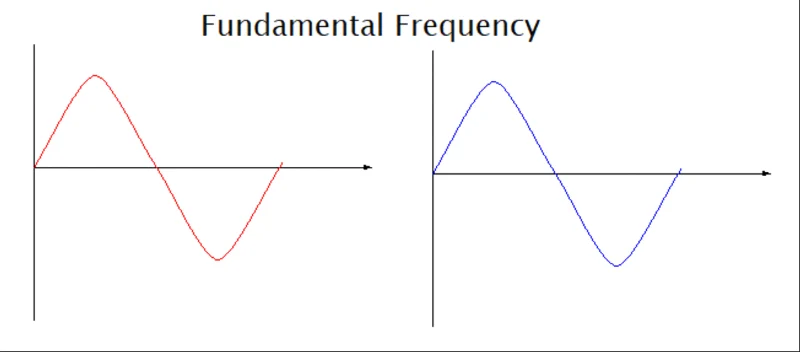
图 1.基波谐波波形。图片由 Simon Mugo 提供
谐波阶次和复数波形 二阶谐波 二阶谐波是频率为 100 Hz 的波形,即 50 Hz 乘以 2。这表明二次谐波的频率是基频的两倍。以下是二次谐波的波形。
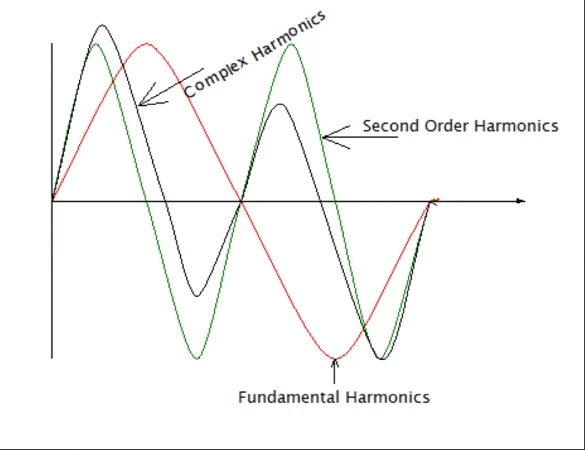
图 2.二阶谐波波形演示。图片由 Simon Mugo 提供
从上面的波形图中可以看出,当基波谐波达到零时,它会达到其高值,依此类推。这就是二次谐波启动相反方向的原因,这意味着负序电流在给定的电路中流动。负序电流会影响感应电动机,它与旋转磁场相反。反对的结果是电机产生的机械扭矩低于预期。这种类型的谐波也称为负序列。
三阶谐波 其频率是基波谐波的三倍。频率为 150 Hz。这是一种非常危险的谐波类型。下面是它的波形。

图 3.三阶谐波波形。图片由 Simon Mugo 提供
从图中可以看出,三次谐波电流和基波电流同时达到零。它们都以相同的值获得高点,但点彼此相反。这个动作使谐波产生零序电流,导致电力系统的中性电压增加。增加中性线电压会导致
继电器操作
断路器。这种效应是由三次谐波电流引起的。三次谐波也称为三重
透镜。
四阶谐波
其频率为 200 Hz,是基频的四倍。下面是波形图。
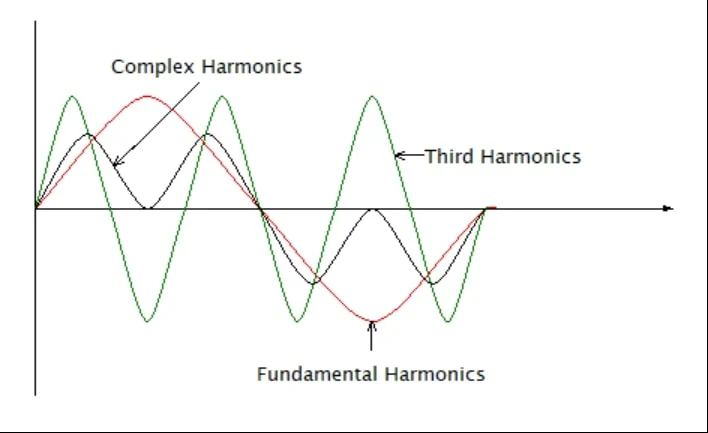
图 4.四次谐波波形。图片由 Simon Mugo 提供
当基波谐波电流达到值时,第四次谐波也会执行相同的操作。从图中可以看出,消极面和积极面都是如此。这就是为什么这种谐波会增加流经导体的电流,从而提高设备温度的原因。它也被称为正谐波。
五次谐波
五次谐波的频率为 250 Hz,特性与三次谐波相似,但工作频率更高。以下是谐波的波形。
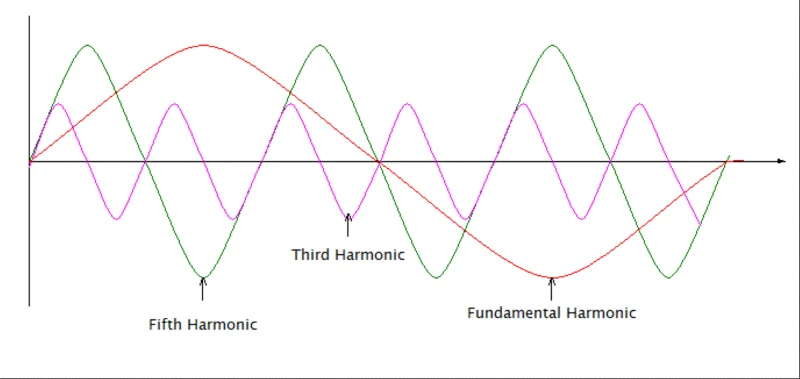
图 5.五阶谐波波形。图片由 Simon Mugo 提供
波形分析
从上面的波形可以清楚地看出,复数波形由谐波和基波的组合组成,每个波形都有自己的相位角和拾取值。
举一个简单的例子,如果我们给出的基频为 E=Vmax(2πft),我们可以计算谐波的值,如下所示。
二次谐波
\[E_{2}=v_{2()}(2\times2\pi ft)\]
\[E_{2}=v_{2()}(4\pi ft)\]
\[E_{2}=v_{2()}(2\omega t)\]
三次谐波
\[E_{3}=v_{3()}(3\times3\pi ft)\]
\[E_{3}=v_{3()}(6\pi ft)\]
\[E_{3}=v_{3()}(3\欧米茄 t)\]
四次谐波
\[E_{4}=v_{4()}(4\times2\pi ft)\]
\[E_{4}=v_{4()}(8\pi ft)\]
\[E_{4}=v_{4()}(4\omega t)\]
其中 2πf=ω
这个过程会一直持续下去,直到更高阶的谐波。
因此,复数波形的方程可以推导出为
\[E_{T}=E_{1}+E_{2}+E_{3}+............+E_{n}\]




