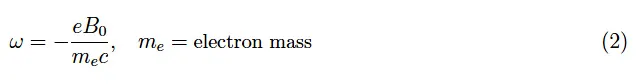霍尔效应确定了
电子和空穴的迁移率,霍尔效应包括使
半导体处于均匀的静磁场中。为了测量载流子的有效质量,除了静磁场之外,还应用射频电磁场来推广该技术。
为了使实验可行,有必要分析研究均匀静磁场中带电粒子(电子或空穴)的行为。由于涉及“微观”量,测量单位使用高斯体系,而不是国际体系(或合理化的MKS体系)。提醒一下,下表很有用:

回旋频率
在霍尔效应的研究中,我们看到磁场通过洛伦兹力弯曲载流子的轨迹,洛伦兹力在高斯系统中由下式给出:

其中:v是粒子的速度,c是真空中的光速,q是电荷,B 0是均匀静磁场。不失一般性,让我们参考电子,因此q = e。
确定受洛伦兹力作用的带电粒子轨迹问题的解决方案在经典电动力学中是众所周知的1。然而,我们遵循了特定的程序2,这应该不足为奇,因为我们仍然需要对牛顿第二定律得出的微分方程进行积分。简而言之,任何电动力学问题都可以简化为动力学问题。具体来说,我们考虑了非相对论运动,即v c,因为我们考虑了半导体物理学中的应用,其中电荷以低于光速的速度移动。
符号。严格来说,应该从量子力学的角度来处理这个问题。这是由俄罗斯物理学家 LD Landau 完成的,如参考文献3中所述。
回到方程(1),我们选择了参考系( Oxyz ),其原点位于电子的初始位置,z轴位于B 0方向和方向。从方程(1)我们看到,如果电子初处于静止状态,它将保持这种机械状态。为了对运动微分方程进行积分,我们使用了数学分析中众所周知的程序,然后比较了通过软件(Mathematica)获得的结果。轨迹是圆柱螺旋线,其轴为平行于 B 0 的直线,因此平行于z轴,并以半径为R的圆为基,该圆取决于沿x轴和y轴的初始速度的分量,以及具有角频率量纲的量ω (图 1):
电力电子科学笔记:利用回旋共振测量有效质量
更准确地说,半径R取决于 | ω |即运动在坐标平面xy上的投影沿着半径R的圆周运动的角速度的。我们称ω c = | ω |电子回旋频率,而R被称为拉莫尔半径。这些结果直观地显而易见:电子轨迹“包裹”了磁场B 0的方向;在带正电荷的情况下,轨迹不会改变。改变的是包裹的方向。
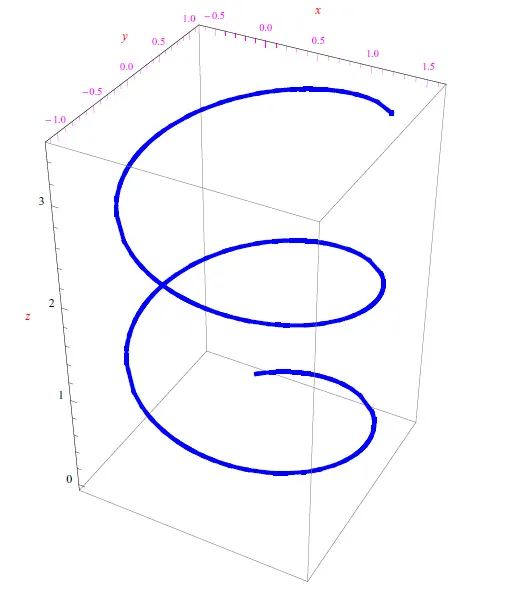
图 1:均匀静磁场中电子轨迹的软件重建。笛卡尔轴上的坐标值是指示性的
所有这一切都是为了一个孤立的电子。对于电子位于半导体导带中的情况,由于与晶格势能的相互作用,问题变得更加复杂。但我们已经学会用有效质量的技巧来绕过这个阴险的问题,使回旋频率变成(符号的明显含义):

类似地,定义了价带孔的回旋频率。如果对于给定的磁场B 0,我们可以测量回旋
加速器频率,从方程(3)我们可以确定有效质量。
回旋共振
实验的初始配置涉及受到均匀
静磁场B 0作用的
半导体晶体。然后发送平坦且单色的电磁波,该电磁波是圆
偏振的,其传播矢量平行且与磁场一致。然后,随着波的频率ω
的变化,测量晶体对电磁场的吸收A。吸收曲线具有图2的趋势,并且是共振过程的典型行为。换句话说,吸收峰出现在ω = ω c时,因此称为回旋共振。
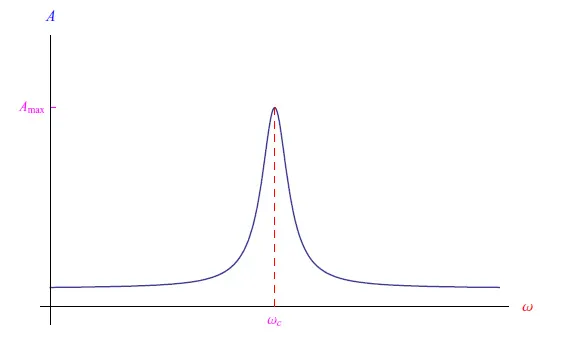
图 2:入射到半导体晶体上的电磁场的典型吸收曲线
让我们研究一下吸收峰宽度γ的物理意义。我们在前几期中已经看到,在德鲁德-洛伦兹模型中,金属的传导电子(或半导体导带中的电子)的运动由与晶格(或半导体导带中的电子)的随机连续非弹性碰撞组成。对抗杂质),平均频率等于 1 /τ r,其中τ r是弛豫时间(在室温下约为 10 -14 s)。
另一方面,在上一节中,我们表明,在存在磁场 B 0的情况下,单个电子的轨迹环绕磁场,将其自身投影到垂直于磁场的平面上,在由相应的角速度ω c的投影,这正是回旋加速器频率。在前面提到的德鲁德-洛伦兹模型中,我们必须通过引入新的弛豫时间τ γ来考虑与晶格的碰撞,然而,在没有磁场的情况下,该弛豫时间 τ γ与弛豫时间τ r 成正比。由于吸收线的宽度γ具有频率的量纲,因此我们期望其倒数 γ1 恰好为 τ。这个结论在数学上通过以下运算得到证实:

电力电子科学笔记:利用回旋共振测量有效质量
这是物理现实中不会发生的两种极端情况。然而,结论是正确的,这意味着我们的解释是正确的。简而言之,通过增加碰撞频率,曲线会变宽,并且测量吸收峰和回旋加速器频率变得更加困难。由此可见,良好的 ωc 测量需要极其纯净的半导体晶体,电子/空穴的浓度不能过高(以降低与晶格碰撞的概率,从而降低频率)。
这可以通过将半导体置于比室温相对较低的温度来实现。此外,为了更加定量,实验成功的一个必要条件是γ -1 > 2 π/ω,其中第二个成员是电子轨迹投影在垂直于圆周的平面上的旋转周期。磁场。事实上,如果上述不等式得到验证,电子就会在经历新的碰撞之前完成完整的缠绕。
至于ω c的数值,通常在无线电波或微波范围内,因此在后一种情况下,半导体被浸入低温谐振腔中。磁场强度为 10 4 G量级。