E 类放大器概述
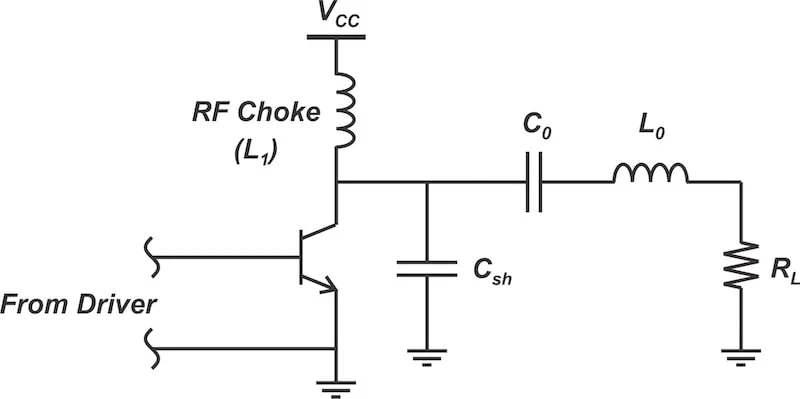
图 1 显示了基本 E 类阶段的拓扑结构。
一个非常基本的 E 类放大器的原理图。
图 1.一个非常基本的 E 类放大器的原理图。
E 类放大器的发明者初将其定义为满足以下条件的
开关模式电路:
开关电压的上升延迟到
晶体管关断之后。
当开关打开时,开关两端的电压为零。
在开关关闭的瞬间,开关电压的斜率也为零。
我们现在将其称为零电压开关 (ZVS) E 类放大器——图 1 显示了该系列中复杂性的成员。还有零电流开关 (ZCS) E 类放大器,它们将上述条件应用于开关电流而不是开关电压,但我们今天不会讨论它们。
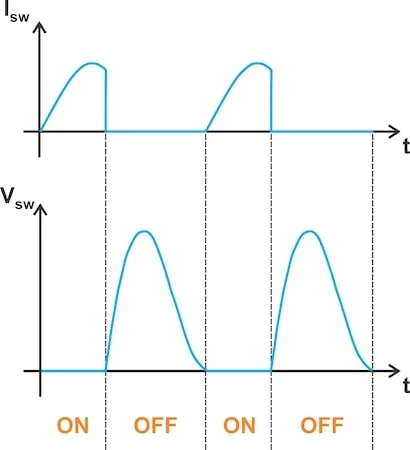
图 2 显示了图 1 中电路的典型开关波形。
ZVS E 类放大器中的典型开关电流 (顶部) 和电压 (底部) 波形。
图 2.ZVS E 类放大器中的典型开关电流 (顶部) 和电压 (底部) 波形。图片由 Steve Arar 提供
正如文章引言所指出的,开关电压 (V西 南部) 或电流为零 (我西 南部) 在任何给定时间。负载网络负责产生适当的电压波形。分流电容 (Csh) 的 S Git,使其足够大以延迟V西 南部直到开关电流降至零。
当开关关闭时,电路减少为阻尼二阶系统,其电感和电容器中存储了一些初始能量(图 3)。该系统中储存的能量是产生V西 南部波形。
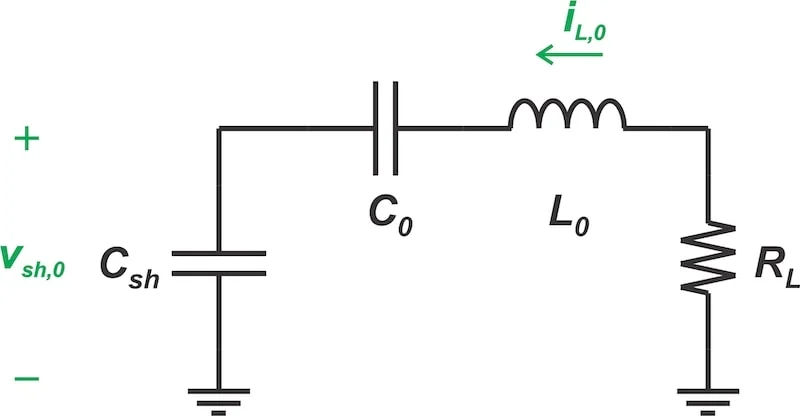
当开关关闭时,E 类放大器的负载网络。
图 3.开关关闭时 E 类放大器的负载网络。图片由 Steve Arar 提供
根据元件值,图 3 中的电路可以产生三种不同类型的瞬态响应:过阻尼、临界阻尼和欠阻尼。图 4 显示了具有一些任意元件值和初始条件的串联 RLC 电路的瞬态响应。
串联 RLC 电路表现出的欠阻尼、临界阻尼和过阻尼响应。
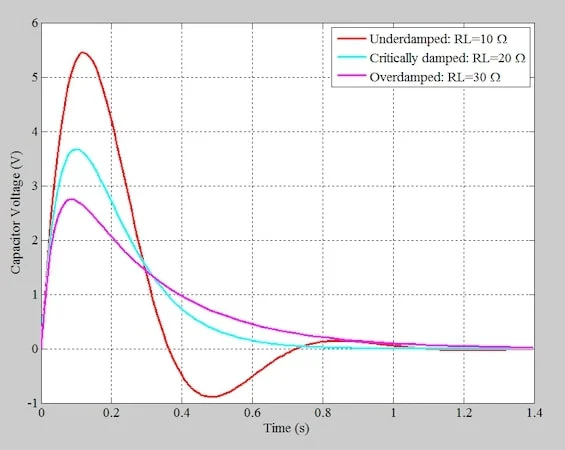
图 4.串联 RLC 电路可以产生过阻尼、临界阻尼和欠阻尼响应。图片由 Steve Arar 提供
什么类型的响应可取?让我们看一下下一节。
了解瞬态响应
从电路论课程中,我们知道二阶系统的自然响应是由其特征方程的根决定的。对于串联 RLC 电路,根为: s = ?α ± j√ω20 ? α2方程 1.
哪里:
? =R2L
?0 = √1LC
根的位置 s1和 s2在 S 平面上,如图 5 所示,帮助我们了解电路的行为。
s 平面上二阶系统的根。
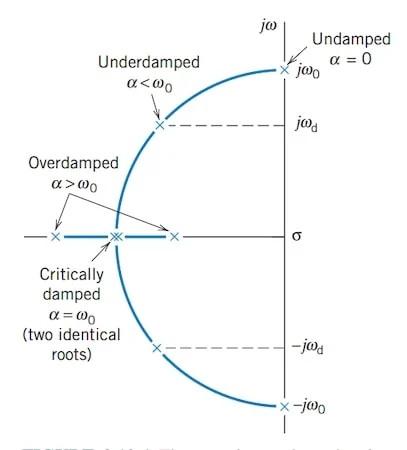
图 5.s 平面上二阶系统的根。图片由 Richard C. Dorf 提供
从公式 1 中,很容易验证过阻尼系统 (>0)具有两个截然不同的真实根源。临界阻尼系统 ( = 0),但是,会生成两个相同的根。在图 5 中,我们观察到临界阻尼系统的相同根位于过阻尼系统的两个根之间。换句话说,过阻尼系统导致更接近 jω 轴的根。
过阻尼系统的瞬态响应是两个衰减指数函数之和,其中衰减率由根值决定。越靠近 jω 轴的根产生一个指数项,该指数项的衰减速度较慢。与临界阻尼系统相比,这个根可以主导瞬态响应,并使系统的响应速度更慢。这与我们在图 4 中看到的情况一致,很明显,临界阻尼系统更快地接近终值。
,虽然过阻尼和临界阻尼系统的根是真实的,但欠阻尼系统 ( <0) 产生复杂的共轭根。这导致了指数阻尼的正弦振荡,如图 4 的红色曲线所示。
E 类负载网络的性能
这一切对 E 类放大器的负载网络意味着什么?首先,如果我们使用过多的阻尼,响应会很慢。如果太慢,当开关打开时,开关两端的电压可能不会归零,从而导致功率损失。过阻尼网络还可能导致二次击穿,当集电极-发射极电压和集电极电流同时存在时,就会发生这种晶体管故障。
另一方面,如果阻尼太小,电路的振荡行为会导致开关导通瞬间出现负电压。如果集电极电压低于驱动器提供的基极 OFF 电压,晶体管可能会进入反向活动模式。在这种模式下,可能会损坏晶体管,但不确定。它还可以增加放大器的功率耗散。
当负载网络作为临界阻尼网络运行时,可实现 E 类级的性能。在这种情况下,V西 南部尽快达到 0 V,而不会表现出任何振荡行为。此外V西 南部接近 0 V,斜率为零。您可能还记得本文开头的内容,这是 ZVS E 类放大器的两个必要条件。
现在我们已经了解了瞬态响应,让我们回顾一下 E 类放大器的设计方程并举一个例子。
设计方程式
计算 E 类放大器中的电压和电流波形比 D 类放大器要复杂一些。在这里,我们将看看终的设计方程。我们将把他们的数学推导留到以后的文章中。
在 50% 的占空比下,调谐电路应在基频下提供电感元件,以产生 E 类波形。负载网络在基频处应呈现的阻抗由下式给出: ZL = RL × (1 + j1.1525) 方程 2.
哪里RL是负载电阻。
与我们研究过的其他放大器类别不同,工作频率下的负载电抗不为零。相反,正如我们在上面的方程式中看到的那样,它实际上与RL.还值得注意的是ZL与输入驱动电平和集电极电源电压无关。
分流电容 (Csh) 由下式给出:
Csh = 12πfRL × 5.447
5.447
方程 3.
其中 f 是操作频率。如果不满足公式 3,则输出功率将不理想。晶体管的本征输出电容本身通常不够大,我们需要增加一些额外的分流电容才能达到所需的值。
使用Csh,我们可以计算出所需的串联电容 (C0) 和电感 (L0): C0 = Csh × 5.447Q × (1 + 1.42Q ? 2.08)
方程 4.
L0 = QRL2πf
方程 5.
其中 Q 是电路的品质因数。为了限度地提高效率,我们通常选择满足应用程序带宽要求的 Q。
,的RL与输出功率 (P外) :
RL = 0.577 × (Vcc ? Vs一个t)2Pout
方程 6.
哪里V坐是晶体管的饱和电压。
封装寄生效应和晶体管的非线性输出电容使得在高频下找到元件值变得具有挑战性。尽管如此,一旦我们选择合适的 Q 因子,使用上述公式设计 E 类
功率放大器通常非常简单。在下一节中,我们将通过一个设计示例来熟悉该过程。
示例:设计 E 类放大器
我们指定一个 E 类放大器的器件额定值和元件值,该放大器在 1 MHz 时为 50 Ω负载提供 1.66 W 的功率。假设一个理想的晶体管,其中V坐= 0 且输出电路的 Q 为 10。
首先,我们使用公式 6 确定所需的电源电压:
RL = 0.577 × (Vcc ? Vs一个t)2Pout50 = 0.577 × (Vcc ? 0)21.66Vcc = 12 V
Csh = 12πfRL × 5.447 = 12π × 1 × 106 × 50 × 5.447 = 584 pF 方程 7.
然后,我们应用公式 3 来找到所需的分流电容:
C0 = Csh × 5.447Q × (1 + 1.42Q ? 2.08)C0 = 584 pF × 5.44710 × (1 + 1.4210 ? 2.08)C0 = 374 pF
方程 8.
,我们通过将刚才找到的值分别代入公式 4 和 5 来计算串联电容和电感:
C0 = Csh × 5.447Q × (1 + 1.42Q ? 2.08)C0 = 584 pF × 5.44710 × (1 + 1.4210 ? 2.08)C0 = 374 pF
方程 9.
L0 = QRL2πf = 10 × 502π × 1 × 106 = 79.6 μH
总结我们的结果,我们有:
电源电压为 12 V (V抄送= 12 V)。
分流电容为 584 pF (Csh= 584 pF)。
A 级电容为 284 pF (C0= 374 pF)。
79.6 μH 的串联电感 (L0= 79.6 μH)。
由于输出电压中的电抗元件,E 类级的峰值电压摆幅是电源电压的 3.56 倍。峰值开关电流约为 1.7V抄送/RL.因此,我们的晶体管电压为 47.27 V,晶体管电流为 0.41 A。




