在本文中,我们将讨论另一种 D 类配置:
变压器耦合电压切换 (TCVS)
放大器。TCVS 放大器的原理图如图 1 所示。
变压器耦合电压开关 D 类放大器的示意图。

图 1.变压器耦合电压开关 D 类放大器。
在本文中,我们将探索该放大器的工作原理,分析其性能,并将其与基本的 B 类配置进行比较。为了巩固我们讨论的概念,我们还将在两个示例问题中确定 TCVS 放大器的电路参数。不过,在此之前,让我们先检查一下电路本身。
TCVS 放大器原理图
您可能已经注意到图 1 中的原理图与我们在之前的文章中了解的变压器耦合推挽式 B 类放大器之间存在一些相似之处。为了便于比较,图 2 中重现了推挽式 B 类级的简化图。

变压器耦合推挽式 B 类放大器的电路图。
图 2.变压器耦合推挽式 B 类放大器。
在上述两种配置中,两个
晶体管(Q 1和 Q 2)在输入信号的交替半周期内工作。在任何给定时间只有一个晶体管处于导通状态。为了避免两个晶体管同时导通,中心抽头输入变压器 (T 2 ) 从单端输入信号产生相反极性的驱动信号。
T 2的中心抽头连接到固定偏置电压。在图 2 中,该电压标记为Vbias。对于推挽式 B 类放大器,Vbias的选择应使晶体管的偏置电压适当地略低于其导通点。对于 TCVS 配置,偏置电压为地。
两种类型的
功率放大器都使用输出变压器 (T 1 ) 来合并集电极电流。在图 1 和图 2 中,输出变压器的中心抽头都连接到电源 ( V CC )。一个主要区别是推挽式 B 类级直接连接到负载。另一方面,TCVS 配置通过串联 LC 电路连接到负载。
尽管有上述相似之处,但这两个放大器的工作方式却完全不同。在推挽式 B 类放大器中,晶体管作为电流源工作,在 T 1的次级产生正弦电压。然而,在 TCVS 放大器中,晶体管被驱动得足够硬,可以充当开关,T 1次级的电压信号是方波。
TCVS 放大器如何工作?
首先,让我们考虑一下 TCVS 放大器操作的每个半周期。图 3 中的简化图显示了当上部开关 (S 1 ) 闭合且下部开关 (S 2 ) 断开时的放大器。我们假设晶体管充当理想开关,这就是为什么 S 1和 S 2在本图和后续图中取代了 Q 1和 Q 2 。
当上开关打开且下开关关闭时的 TCVS 放大器。

图 3. S 1开启且 S 2关断时的 TCVS 放大器。
在这个半周期中,节点C明显处于地电位。初级绕组的上段出现V CC的电压降。其极性在图中以紫色显示。
由于变压器的作用,下部绕组也会产生相同的电压。因此,节点 D 的电压为 2 V CC,而节点 C 的电压为地。请注意,我们假设变压器和开关都是理想的。

图 4 示出了下一个半周期,其中 S 1打开而 S 2关闭。
当上部开关关闭且下部开关打开时的 TCVS 放大器。
图 4. S 1关闭且 S 2开启时的 TCVS 放大器。
现在初级绕组下段上出现了V CC电压。绕组之间的磁耦合在初级绕组上段上产生了相同的电压。再次,极性显示为紫色。在这个半周期中,节点 D 接地,节点 C 为 2 V CC。
了解电压波形
回顾一下:
当 S 1处于关闭状态且 S 2处于打开状态时,节点 C 为 2 V CC而节点 D 处于接地状态。
当 S 1为 ON 且 S 2为 OFF 时,节点 C 接地,节点 D 为 2 V CC。
因此,节点 C 和节点 D 处的电压(分别为V C和V D)为在零和 2 V CC之间切换的方波。图 5 显示了两个完整周期内的这些电压波形,假设在个半周期内S 1为 OFF,S 2为 ON。
节点 C(顶部)和节点 D(底部)处的电压。
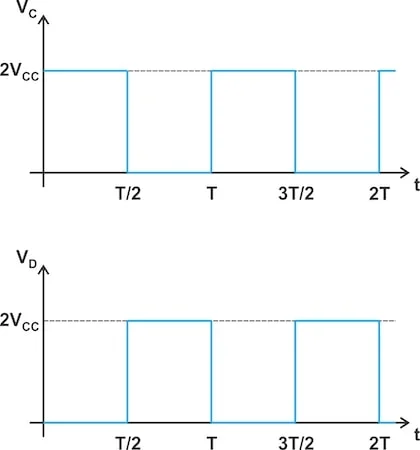
图 5.两个完整运行周期内节点 C(顶部)和节点 D(底部)的电压。
这里的关键点是每个晶体管的集电极-发射极电压是电源电压的两倍 (2 V CC )。在为 TCVS 放大器选择晶体管时应考虑到这一点。
接下来,让我们确定调谐电路输入端(节点 E)的电压。从图 3 和图 4 中,我们观察到,极性交替的V CC电压在初级绕组的每个部分上下降。由于初级绕组中的每个部分都有m匝,而次级绕组有n匝,因此节点 E 处的电压幅度为 ( n / m ) V CC。由于极性在一个半周期中为正,在另一个半周期中为负,因此节点 E 处的电压在 +( n / m ) V CC和 –( n / m ) V CC之间切换。
这其实是 TCVS 电路的一个优点。通过改变输出变压器的匝数比,我们可以根据设计规范调整输出方波的幅度。节点 E ( V E ) 的电压波形如图 6 所示。
两个完整运行周期内节点 E 处的电压。
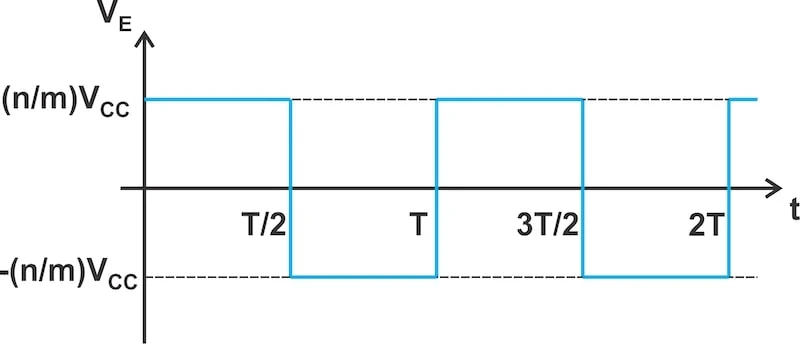
图 6.两个完整运行周期内节点 E 处的电压。
TCVS 电路的操作与图 7 中的基本 D 类放大器的操作非常相似。
基本 D 类放大器的图表。

图7.基本D类放大器。
这是我们用来介绍D 类操作概念的同一个简单电路。在这里,与 TCVS 放大器一样,S 1和 S 2交替打开和关闭以在节点 E 产生方波。但是,方波在地和V CC之间切换,而不是在 +( n / m ) V CC和 –( n / m ) V CC之间切换。
现在我们了解了 TCVS 放大器的工作原理,让我们来检查一下它的性能。
查找 TCVS 放大器的输出功率
放大器的串联 RLC 电路对输入电压的基频分量(除基频分量外)都表现出非常大的阻抗。因此,调谐电路会在基频处施加正弦电流(图 8)。
基频的正弦电流流过RLC电路。
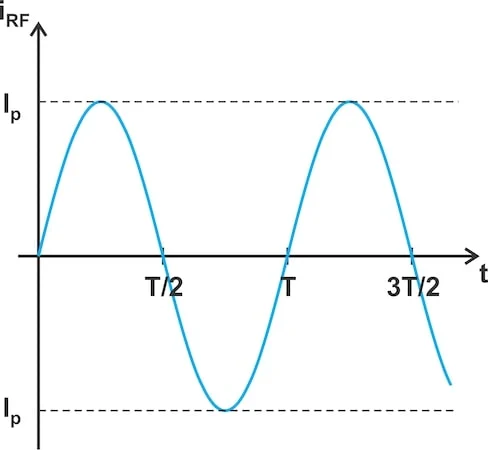
图 8.基频的正弦电流流过 RLC 电路。
要找到 TCVS 放大器输出电流的幅度,我们需要找到节点 E 处的方波的基波分量。使用傅里叶级数表示,我们可以用其组成频率分量来表示图 6 中的方波电流:
$$v_E~=~\frac{4}{\pi} \frac{n}{m}V_{CC} \sum_{p=1}^{\infty}\frac{\sin((2p~-~1)\omega_{0}t)}{2p~-~1}$$
等式 1.
在哪里:
n = 输出变压器次级绕组的匝数
m = 输出变压器初级绕组每段的匝数。
因此,方波的基波分量的峰值为:
$$v_{E, \ fund}~=~ \frac{4}{\pi}\frac{n}{m} V_{CC}$$
等式 2.
除以R L,我们可以得出输出电流的峰值:
$$I_p ~=~ \frac{4}{\pi}\frac{n}{m} \frac{V_{CC}}{R_L}$$
等式 3.
终输出功率为:
$$P_{L} ~=~ R_Li_{rms}^2 ~=~ \frac{8}{\pi^2} (\frac{n}{m})^2 \frac{V_{CC}^2}{R_L}$$
等式 4.
其中i rms = I p /\(\sqrt{2}\)。
公式 3 和公式 4 是设计 TCVS 放大器的关键关系,我们稍后会看到。同时,让我们找出 TCVS 放大器的理论效率。
确定 TCVS 放大器的效率
要计算放大器的效率,我们需要知道输出功率(公式 4)和输入功率。输入功率等于电源电压乘以电源电流的平均值。
虽然输出电流 ( i RF ) 是正弦波,但流过开关的电流(图 1 中的i 1和i 2)是半波整流正弦波。因此,从电源抽取的总电流 ( i cc ) 是全波整流正弦波。该电流波形如图 9 所示。
从电源吸取的总电流是全波整流正弦波。

图 9.从电源吸取的总电流是全波整流正弦波。
尽管iRF的峰值为Ip ,但icc的峰值为 ( n / m ) Ip 。这是由于变压器的电流缩放功能。您可以轻松验证幅度为 Ip 的全波整流正弦波具有2Ip / π的直流分量。图 9 中幅度为(n / m ) Ip的波形的平均值是:
$$I_{dc} ~=~ \frac{2}{\pi} \big ( \frac{n}{m}I_p \big )$$
等式 5.
乘以V CC并代入公式 3 中的I p后,可得出电源输送的功率为:
$$P_{CC} ~=~ \frac{8}{\pi^2} \Big ( \frac{n}{m} \Big )^2 \frac{V_{CC}^2}{R_L}$$
等式 6.
这等于公式 4 中的输出功率,这意味着 TCVS 放大器(与互补电压开关放大器一样)的理想效率为 100%。
示例 1:选择 TCVS 放大器的晶体管电压和电流
在上一篇文章中,我们找到了基本 D 类放大器(图 7)的电源电压和开关电流,该放大器向 50 Ω 负载提供 20 W 功率。让我们针对理想 TCVS 放大器重复此示例,该放大器向 50 Ω 负载提供 20 W 功率。假设匝数比 ( n / m ) 为 1。
我们从电源电压开始。将示例值代入公式 4,可得出:
$$P_{L} ~=~ \frac{8}{\pi^2} (\frac{n}{m})^2 \frac{V_{CC}^2}{R_L} ~~\rightarrow~~20 ~=~ \frac{8}{\pi^2} ~\times~ 1 ~\times~ \frac{V_{CC}^2}{50}$$
等式 7.
求解V CC,我们得到:
$$V_{CC}~=~ \sqrt{\frac{1000}{8} \pi^2}~=~35.1$$
等式 8.
TCVS放大器的电源电压为35.1V。
从图 9 可以看出,流过开关的电流为 ( n / m ) I p。代入公式 3 中的I p,我们可得出:
$$I_{max} ~=~ \frac{4}{\pi}(\frac{n}{m})^2 \frac{V_{CC}}{R_L}$$
等式 9.
我们知道V CC = 35.1 V、( n / m ) = 1 和R L = 50 Ω。将这些值代入公式 9,我们得到:
$$I_{max}~=~(\frac{4}{\pi})(\frac{35.1}{50})~=~0.89$$
等式 10。
TCVS 放大器的开关电流为 0.89 A。
TCVS 放大器与基本 D 类放大器
回想一下,我们之前使用基本 D 类放大器而不是 TCVS 放大器完成了示例 1。这为我们提供了一个有用的起点来比较这两种设计,正如我们将在本节中看到的那样。
给定输出功率的电源电压和开关电流
总结上一节的结果,对于向 50 Ω 电阻负载输出 20 W 功率的 TCVS 放大器, V CC = 35.1 V 和I max = 0.89 A。对于相同的输出功率和负载电阻,基本 D 类放大器需要 70.2 V 的电源电压。与 TCVS 放大器一样,其每个开关的电流为 0.89 A。换句话说,TCVS 配置允许我们在使用相同电流的同时将电源电压减半。
TCVS 放大器如何实现这一点?假设n / m = 1,TCVS 电路在调谐电路的输入端产生峰峰值为 2 V CC的方波。另一方面,基本 D 类放大器产生峰峰值为V CC。这允许 TCVS 电路在给定输出功率和负载的情况下将电源电压减半。
集电极-发射极电压
那么集电极-发射极电压又如何呢?在基本的 D 类配置中,集电极-发射极电流等于V CC,即 70.2 V。但是,图 5 中的波形显示 TCVS 电路中的集电极-发射极电压是电源电压 (2 V CC ) 的两倍。因此,虽然我们可以在 TCVS 设计中使用V CC = 35.1 V的电源电压,但晶体管应承受的集电极-发射极电压为 70.2 V — 与基本 D 类设计相同。
固定电源的开关电流和输出功率
,假设我们保持电源电压和负载电阻不变。基本D类放大器和TCVS放大器的开关电流和输出功率有何变化?
从首先介绍该配置的文章中,我们知道基本 D 类放大器的开关电流为:
$$I_{max} ~=~ \frac{2V_{CC}}{\pi R_L}$$
等式 11.
如果我们将其与 TCVS 放大器的开关电流(公式 9)进行比较,我们会发现,对于给定的电源电压(假设n / m = 1),TCVS 电路所需的电流是基本 D 类放大器的两倍。同时,基本 D 类放大器的输出功率为:
$$P_{L} ~=~ \frac{2V_{CC}^2}{\pi^2 R_L}$$
等式 12.
公式 4 和公式 12 表明,对于相同的电源电压和负载阻抗,TCVS 电路的输出功率是基本 D 类放大器的四倍。我们再次假设n / m = 1。
但是如果n / m不等于 1 会怎样?TCVS 电路中输出变压器的匝数比为我们提供了一个额外的设计参数。正如我们的下一个示例将说明的那样,此参数可用于权衡电源电压和开关电流。
示例 2:了解输出变压器的作用
假设 TCVS 放大器要为 50 Ω 负载提供 20 W 功率,如上例所示。然而,匝数比现在为n / m = 2。所需的电源电压和开关电流是多少?
将上述值代入公式 4,我们得到:
$$P_{L} ~=~ \frac{8}{\pi^2} (\frac{n}{m})^2 \frac{V_{CC}^2}{R_L} ~~\rightarrow ~~20 ~=~ \frac{8}{\pi^2} ~\times~ 2^2 ~\times~ \frac{V_{CC}^2}{50}$$
等式 13.
求解V CC可得出:
$$V_{CC}~=~\sqrt{\frac{1000}{32} \pi^2}~=~17.56$$
等式 14.
电源电压为V CC = 17.56 V,是上例中所得值的一半。开关电流为:
$$I_{max} ~=~ \frac{4}{\pi}(\frac{n}{m})^2 \frac{V_{CC}}{R_L} ~~\rightarrow~~ I_{max} ~=~ \frac{4}{\pi} ~\times~ 2^2~ \times~ \frac{17.56}{50}~=~1.79$$
等式 15.
Imax = 1.79A,是之前值的两倍。简而言之,匝数比加倍可将所需电源电压降低两倍,并将电流增加相同倍数。








