降低
功率放大器的导通角可以提高其效率。A 类
放大器的导通角为 360 度,理论效率为 50%;B 类放大器的导通角为 180 度,效率为 78.5%。
这种效率提高的趋势在C 类放大器中得以延续,其导通角低于 180 度。例如,如图 1 所示,导通角为 90 度的 C 类放大器的理论效率为 94%。
效率与导通角。导通角为 90 度时,效率为 94.04%。
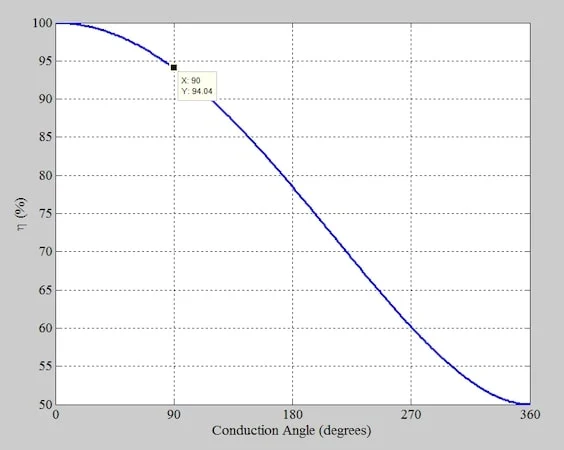
图 1.效率与导通角的关系图。
不幸的是,C 类功率放大器有几个缺点,限制了它们在现代固态射频电路中的应用。首先,在相同的输入功率下,它们产生的输出功率比 A 类或 B 类放大器要小得多。如果我们研究输出功率与 A 类或 B 类放大器相同的C 类放大器的设计,就会发现更多的限制。
在本文中,我们将通过比较 A、B 和 C 类放大器的性能来探索这些限制,这些放大器必须向给定的负载阻抗提供一定的射频功率。为简单起见,我们将在整篇文章中对 C 类放大器使用 90 度导通角。让我们首先比较每个放大器的输出
晶体管承载的电流。
晶体管电流要求
在上一篇文章中,我们了解了导通角如何改变输出电流的频率内容。您可能从该讨论中认出了图 2。它绘制了 A、B 和 C 类放大器的平均 ( a 0 ) 和基波 ( a 1 ) 分量与导通角的关系。为了使这三种设计能够提供相同的功率,它们各自的输出电流应具有相同的基波分量。
输出电流的平均分量和基波分量与导通角的关系图。
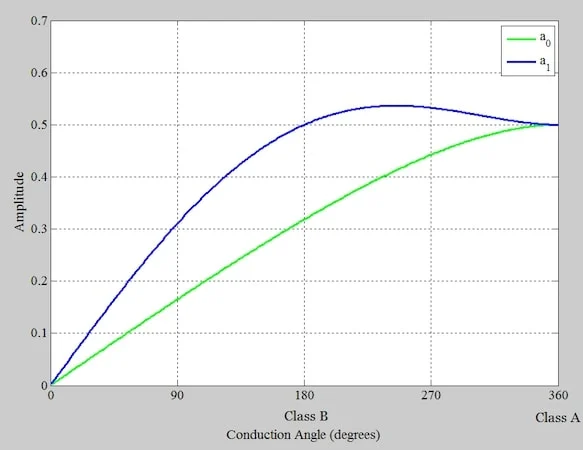
图 2.平均和基波分量与导通角的关系。
请注意,此图中的a 0和a 1系数已归一化为I M,其中I M是晶体管电流的峰值。换句话说,I M假定为 1。
A类晶体管电流
假设 A 类放大器中的晶体管电流为I MA 。从图 1 中我们可以看出,以I MA为标准的 A 类放大器的基波分量为 0.5。因此,我们有:a1IMA = 0.5 → a1 = 0.5IMA 等式 1.
如果您不能立即弄清楚为什么基波分量是 A 类放大器电流的一半,请记住,这种类型的放大器将晶体管偏置在其负载线的中点。放大器的集电极电流是偏置电流和交流电流的总和。
为了获得的对称摆幅,流过晶体管的直流电流应等于传送到负载的交流电流的幅度。图 3 显示了当晶体管达到其负载线的边界时 A 类放大器中的集电极电流如何变化。
在具有对称摆幅的 A 类级中,集电极电流从 0(a)变为 RF 电流的两倍(b)。
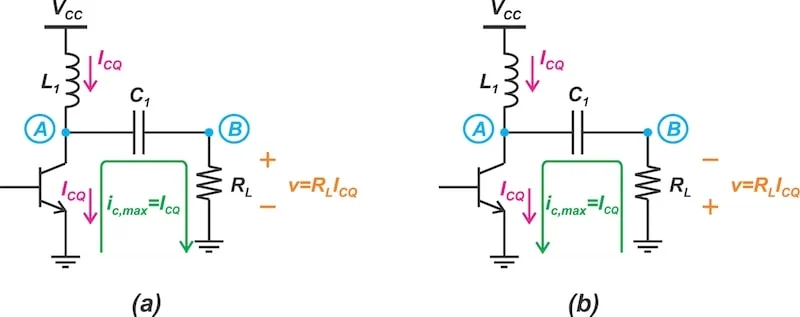
图 3. 具有对称摆幅的 A 类级中的(a)和(b)集电极电流。
如您所见,集电极电流从零变为 RF 电流的两倍。这与公式 1 一致。
B 类晶体管电流
那么 B 类放大器呢?假设 B 类放大器的集电极电流为I MB。图 1 显示,B 类放大器的归一化基波分量也是 0.5,从而得出:
a1IMB = 0.5 → a1 = 0.5IMB 等式 2.
由此我们看到,对于给定的晶体管电流,A 类和 B 类放大器产生相同的基本分量。
C 类晶体管电流
C 类放大器的基波分量取决于其导通角。我们假设导通角为 θ c = 90 度,这对应于归一化基波分量 0.31(图 1)。因此,我们有: a1IMC = 0.31 → a1 = 0.31IMC 等式 3.
其中,I MC是丙类放大器的集电极电流。
比较晶体管电流
总结一下:
对于 A 类放大器,a1 = 0.5IMA 。
对于B类放大器,a1 = 0.5IMB 。
对于 C 类放大器,a 1 = 0.31 I MC
为了使这三种设计产生相同的基本组件,必须满足以下条件:
0.31IMC = 0.5IMA = 0.5IMB 等式 4.
求解I MC,我们得到:IMC = 1.6IMA = 1.6IMB 等式 5.
C 类放大器的峰值电流是 A 类或 B 类放大器的 1.6 倍。请记住,我们的计算基于具有 90 度导通角的 C 类放大器。导通角小于 90 度的 C 类放大器相对于 A 类或 B 类放大器的峰值电流甚至更高。
这里的关键点是,C 类放大器中的晶体管必须处理更大的电流才能产生相同的输出功率。实际上,这意味着放大器需要更大的晶体管。我们越减小导通角,峰值电流就越高,晶体管就需要越大。这可能会带来问题——首先,晶体管越大会导致匹配带宽越低。
晶体管尺寸要求是一个主要缺点。还有其他高效功率放大器配置不需要这么大的晶体管,这些配置已在现代固态射频设计中取代了 C 类操作。
在选择晶体管时,我们还需要考虑放大器的电压。正如我们将在下一节中看到的那样,C 类放大器的操作在这里也会遇到问题。
反向击穿电压问题
在导通角较小的放大器中,要将输出电流摆动到允许值,需要在晶体管的输入端施加较大的电压。要理解原因,请考虑图 4 中的电压波形。
当使用较小的导通角时,需要较大的输入电压。
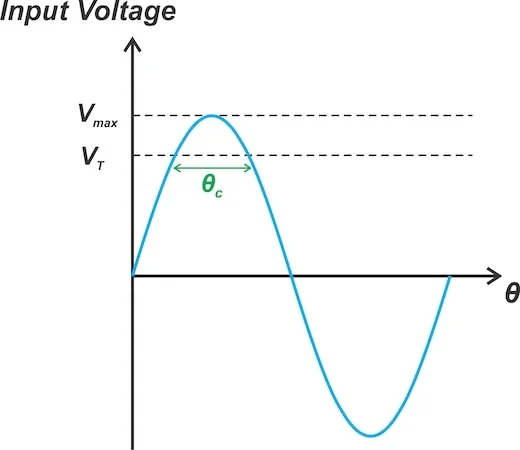
图 4.使用小导通角时需要较大的输入电压。
在上图中:
θ c是放大器的导通角。
V T是晶体管的导通电压。
V max是产生输出电流的输入电压。
V max和V T之间的差值应足够大,以使晶体管在输入为V max时产生电流。但是,输入超过V T的部分仅对应于 RF 周期的一小部分(较小的导通角)。因此需要非常大的驱动信号。
现在考虑输入的负摆幅。当输入电压接近其值时,输出电压会摆至值。这会在集电极-基极
端子之间产生较大的电压,这可能会导致集电极-基极结击穿。这种反向击穿会损坏晶体管,并导致从集电极到发射极的大量不受控制的电流流动。
失真和非线性
要了解传导角如何影响线性度,比较设计为相同输出功率的 A、B 和 C 类放大器的输出电流波形是有益的。这些波形如图 5 所示,可读如下:
紫色曲线对应 360 度导通角(A 类操作)。
洋红色曲线对应 180 度导通角(B 类操作)。
橙色曲线对应 90 度导通角(C 类操作)。
A、B、C 类放大器的电流波形。
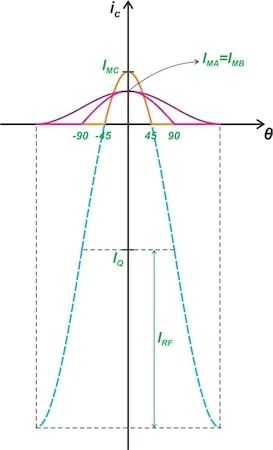
图 5. A 类(紫色)、B 类(洋红色)和 C 类(橙色)放大器的电流波形。
蓝色虚线是幅度为I RF、负偏移为I Q的正弦波。C 类波形是该正弦波的一部分。
正如蓝色曲线所示,当我们使用 360 度以外的导通角时,输出电流仅在周期的一部分中为正弦波段。在周期的其余部分,输出电流为零。由于输入波形是纯正弦波,因此输出波形相对于它显然失真。根据此定义,只有 A 类放大器是线性的。
然而,在功率放大器的背景下,我们也可以根据输出端基波分量的功率如何随输入功率的变化来定义线性。即使放大器涉及高度非线性的过程,其整体输入输出特性仍然可以是线性的。请注意,此线性定义假设输出的所有谐波分量都被输出端的高 Q 谐振电路短路。
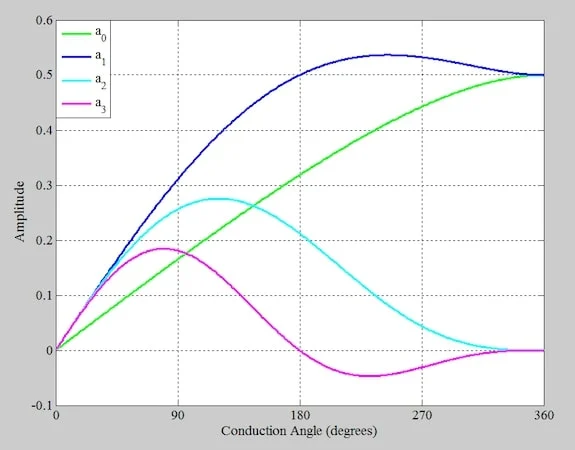
图 6 显示了放大器电流波形的二次谐波和三次谐波(a 2和a 3 )随导通角的变化情况,以及平均和基波分量(a 0和a 1 ) 。利用该图,我们重新检查一下 A 类、B 类和 C 类放大器的线性度。
输出电流的平均值及前三个频率分量与导通角的关系。
图6.输出电流的平均值和前三个谐波频率分量与导通角的关系。
A 类和 B 类放大器的线性度
A 类操作仍被认为是线性的,因为信号没有削波。在图 6 中,第二和第三谐波分量在 360 度导通角处均为零。
B 类级的输入信号相对于晶体管的导通点是对称的。在 180 度导通角处有一个二次谐波分量,但三次谐波为零。改变输入信号的幅度不会影响导通角。
因此,B 类放大器输出端的基波分量功率与输入功率成正比。从这个意义上讲,单晶体管 B 类放大器是线性的。B 类放大器输入驱动功率的降低会导致输出功率的相应降低。
C 类放大器的线性度
对于小于 180 度的导通角(C 类操作),我们在图 6 中看到,存在第二和第三谐波分量。C 类放大器使用更窄的脉冲来实现更高的效率,其导通角随输入信号的幅度而变化。回头参考图 5 应该可以帮助您直观地看到这一点。
对于给定的偏置点,降低输入信号的幅度会降低导通角,从而降低级的增益。这意味着即使我们考虑输出的基波分量与输入功率的关系,C 类放大器也不是线性的。例如,将输入功率降低 3 dB 可能会使输出基波功率降低 3 dB 以上。
AB 类放大器的线性度
另外,AB 类放大器(即导通角在 180 度到 360 度之间的放大器)即使使用完全线性的晶体管,也是非线性的。这是因为放大器的导通角会随着驱动电平而变化。
然而,需要注意的是,现实世界中的晶体管是非线性器件,因此在现实世界中,所有类型的放大器都具有一定的非线性。实践证明,AB 类放大器为幅度调制信号提供线性度。由于 AB 类放大器在效率方面也具有优势,因此它们通常用于涉及幅度调制的应用中。
抑制谐波分量
回到我们讨论的主要话题,C 类工作模式还有一个问题我们还没有提到:即输出电流的谐波分量比 A 类或 B 类放大器的谐波分量要大。当我们使用越来越小的导通角时,情况尤其如此(图 6)。因此,我们需要一个 Q 值更高的谐振电路来抑制谐波分量。





