使用 A 类
放大器时,
晶体管始终处于开启状态。因此,放大器的导通角为 360 度。在B类放大器中,晶体管仅导通信号周期的一半,因此导通角为180度。
我们了解到,减小导通角度可以让我们将效率从A类放大器的50%提高到B类放大器的78.5%。但是,如果我们进一步减小导通角,效率会发生什么变化?
导通角小于 180 度的
功率放大器称为 C 类放大器。在本文中,我们将研究C类放大器的操作,并探讨降低导通角对各种功率放大器性能参数的影响。,我们将通过一个经典的统一分析来比较A类、B类和C类放大器的性能。
C类放大器中的电流和电压波形
在C类放大器中,晶体管导通的时间不到输入周期的一半。在窄脉冲的刺激下,晶体管在输出端产生短电流脉冲。图1中的橙色曲线显示了C类放大器的集电极电流的一个周期,其导通角为θc.
我们可以在上面看到,当晶体管处于活动状态时,输出电流是正弦曲线的一部分,而当晶体管处于截止状态时,输出电流为零。全正弦曲线(上面的蓝色曲线)的负偏移量为我Q和振幅我射频.直流偏置我Q与线性放大器中的偏置电流类似,但在C类放大器中为负。因此,输出电流可以用以下表达式来描述:
其中 θ 对应于水平轴上的位置。
通过改变我Q,我们也可以产生 A 类和 B 类放大器的波形。例如我Q= 0 导致 180 度的导通角(B 类)。因此,我们可以使用上述波形来检查正在讨论的所有三个放大器类别(A、B和C)的性能。

图2比较了近乎完美的A类、B类和C类放大器的晶体管电流和输出电压波形。
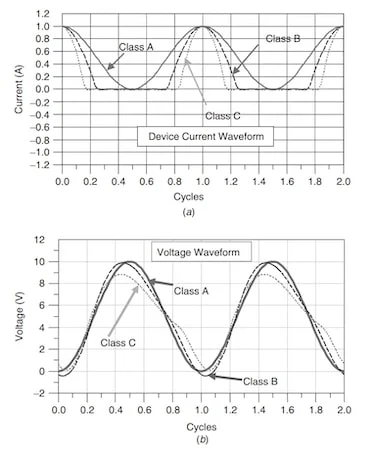
A类、B类和C类放大器的电流和电压波形。
Figure 2. A、B和C类放大器的电流(a)和电压(b)波形。图片由 George Vendelin 提供
A类放大器的晶体管电流和输出电压波形均为正弦曲线。虽然晶体管电流在 B 类和 C 类阶段只是正弦曲线的一部分,但在这些工作模式下,输出电压也可以近似为正弦曲线。这是因为 B 类和 C 类放大器的输出端存在高 Q 谐振腔,我们将在下一节中看到。
C类放大器原理图
图3显示了C类放大器的基本电路原理图。放大器输出端的高 Q 值罐标记为绿色。
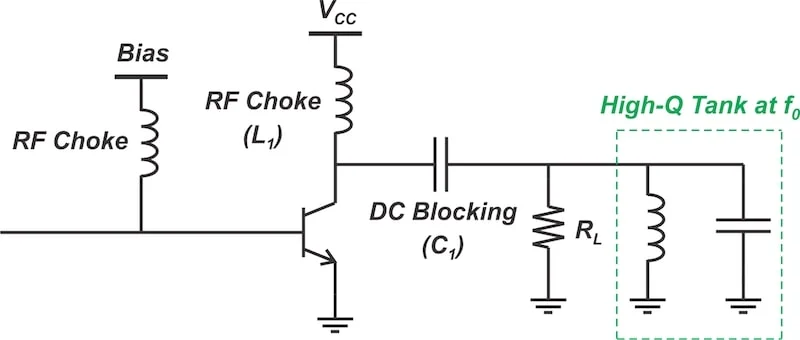
C类功率放大器的基本原理图。它还可用于构建单晶体管 B 类功率放大器。
图3.C类放大器的基本原理图。图片由 Steve Arar 提供
根据我们为晶体管选择的静态偏置点,上述原理图也可用于构建A类级或单晶体管B类级。A类放大器是三种类型中线性度强的放大器,它可能使用Q因子相对较低的谐振电路。
在线性度谱的另一端,C类放大器在输出端产生一连串短电流脉冲。高Q值谐振电路可短路输出电流谐波,并减少由不可避免的非线性引起的带外发射。请注意,高Q值谐振电路必然意味着窄带操作。
波形分析
在分析C类阶段时,我们假设以下几点:
输出电压可以通过正弦波形来近似。这需要一个理想的谐振电路,该电路可以短路输出电流的所有高次谐波。
集电极电流波形是正弦波的一部分。实际上,只有在低频下才是正确的。
虽然在实践中不一定正确,但这些假设使我们能够简化电路分析。考虑到这一点,让我们来看看C类放大器的性能。
由于高 Q 谐振腔,基频的功率是实际传递给负载的功率。因此,为了找到输出功率,我们需要分析输出电流波形的频率成分。我们可以通过改变波形的时间原点来简化这种分析。图 4 是围绕垂直轴对称的,就是结果。

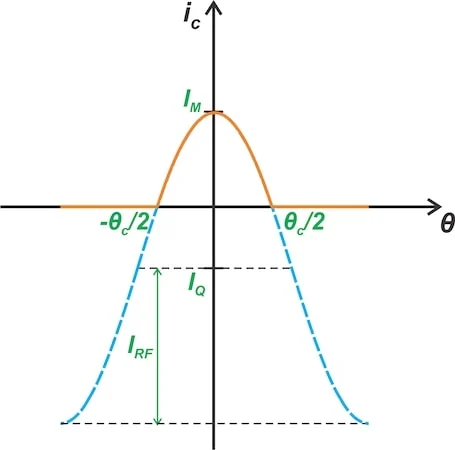
C类放大器中的一个集电极电流周期。
图4.C类放大器中的一个集电极电流周期。图片由 Steve Arar 提供
哪里一个n表示 n 次谐波的傅里叶系数。要找到C类级的效率和输出功率,我们只需要平均值(a0)和基本组成部分(a1) 的电流波形。在不进行所有数学运算的情况下,结果在下面的公式 4 和 5 中提供:
其中 φ 等于导电角的一半 (\(\phi~=~\frac{\theta_{c}}{2}\))。
图5绘制了平均分量和基波分量与导通角的关系图。
平均分量和基本分量与传导角的关系。
图5.平均分量和基本分量与传导角的关系。图片由 Steve Arar 提供

该图显示了 a 的绘图0和一个1系数归一化为我M(或者,等同于我M被假定为统一体)。我们很快就会回到这些结果。首先,我们来计算一下C类放大器的效率。
C 类操作效率
假设高Q谐振器消除了高次谐波分量,则交流输出电压可以由公式5计算得出:
$$v_{out} ~=~ R_L a_1 \cos(\theta)$$
等式 6.
哪里RL是负载的电阻。
因此,输送到负载的平均功率为:
$$P_L ~=~ \frac{(v_{rms})^{2}}{R_L} ~=~ \frac{R_L a_1^{2}}{2}$$
等式 7.
为了计算
电源提供的功率,我们将从电源汲取的电流平均值乘以电源电压。电流的平均值是一个0生产:
在适当的
负载电阻下,电流的基波分量产生允许电压摆幅。电压摆幅的振幅为V抄送.因此,从公式 6 可以看出,当出现以下情况时,可实现效率:
,将等式 4 和 5 代入上述等式可得到:
$$\eta_{max} ~=~ \frac{1}{2} ~\times~ \frac{\phi ~-~ \sin(\phi) \cos (\phi)}{\sin (\phi) ~-~ \phi \cos (\phi)}$$
等式 12.
该方程式如图 6 所示。
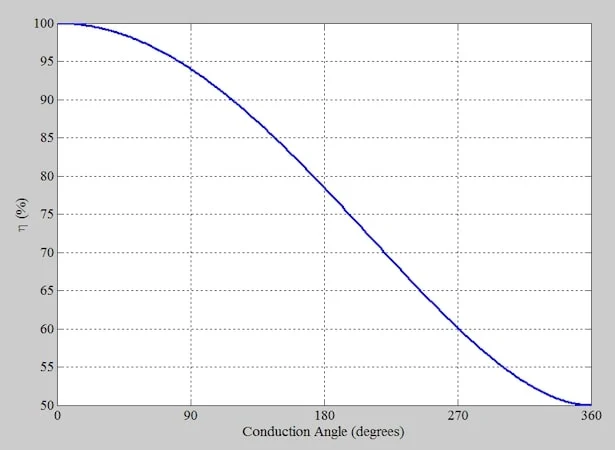
效率与传导角的关系图。
图6.效率与传导角的关系。图片由 Steve Arar 提供
让我们通过一个示例为这些方程式提供一些背景信息。
示例:为C类放大器选择电流规格
我们知道,晶体管在它们可以处理的电压和电流水平以及它们可以燃烧而不会损坏的功率方面受到限制。确定 C 类放大器的晶体管电流,该放大器以 85% 的效率向 50 Ω负载提供 25 W 功率。忽略晶体管的饱和效应,假设电源电压(V抄送) 为 12 V。
输出电流的基本分量(a1) 确定输送到负载的功率。从公式 7 中,我们得到:
在此示例中,我们以效率运行。因此,我们知道RL一个1 = V抄送(公式 10)。因为V抄送=12 V,我们有RL一个1 = V抄送= 12 V。 将12 V值代入公式13,得到基波分量的幅度:
从图7中,我们观察到,从图7中,η麦克斯= 85% 对应于 θc= 147 度。
在 θc = 147 度时可实现 85% 的效率。

图7.在 θ 处可实现 85% 的效率 c= 147 度。图片由 Steve Arar 提供
在 θ 的导通角下c= 147 度,a 的归一化值1为 0.45(图 8)。
在147度的导通角下,归一化基波分量为0.45。

图8.在 θc= 147 度,归一化基波分量为 0.45。图片由 Steve Arar 提供
晶体管应能够处理 9.27 A 的电流。晶体管承受的电压为 24 V,或电源电压的两倍 (2V抄送= 2 × 12 V = 24 V)。
比较 A、B 和 C 类操作
接下来,让我们稍微扩大一下关注范围,看看改变导通角度如何影响以下性能参数:
供电。
输出功率。
效率。
从电源汲取的功率如何随 θ 变化c
随着导通角从360度(A类操作)减小到180度(B类操作)再到0度,输出电流的直流分量单调减小。
如果我们考虑图4中的电流波形,这是有道理的。较小的导通角意味着电流不为零的区域较小,这也对应于较小的平均值。因此,减小导通角会降低平均值和从电源汲取的直流功率。
输送到负载的功率如何随 θ 变化c?
图 5 中的基本组件表现出更有趣的行为。在 360 度时,基本分量值为 0.5。当我们将导通角从 360 度减小到 180 度时,基本分量略有上升。
然而,在 180 度时,基本值再次为 0.5。这意味着,对于相同的晶体管规格和电源电压,A 类和 B 类级产生相同的输出功率。
C类操作区域呢?如果我们将方程式 10 代入方程式 7,我们观察到输出功率与1.从图 5 中,θc接近零,a 也接近零1.因此,C类放大器的输出功率也降至零。这是 C 类操作的一个显着缺点。
C类放大器的效率如何随θ变化c?
在C类区域,随着导通角的减小,平均分量和基本分量都会下降。从公式 11 中,我们知道效率 (η麦克斯)与基本分量与平均值的比率成正比。同时,对图 6 的目视检查证实η麦克斯随着我们减小传导角而增加。当导通角趋近于零时,效率接近100%。
虽然这个结果乍一看似乎令人兴奋,但请记住,在相同输入功率下,C类放大器的输出功率远低于A类或B类放大器的输出功率。例如,在A类放大器中,如果配置产生的功率是同一器件的一半,即使其效率高达95%,也几乎没有实际用途。
C类放大器的缺点
C 类配置还存在其他几个限制:
对于给定的输出功率,C类放大器中使用的晶体管必须比A类或B类放大器中的晶体管处理更大的电流。随着我们减小传导角以实现更高的效率,这种情况会变得更糟。
更大的电流意味着我们需要更大的设备,这会导致较低的匹配带宽。
C类配置比A类或B类放大器更具非线性性。
C类级需要具有更高击穿电压的晶体管。
与A类或B类放大器相比,C类放大器需要更高Q值的谐振电路来抑制谐波分量。








