使用完整的波形来设计磁性对于优化至关重要。 设计电源可能是一项艰巨的任务,因此工程师将问题分解为更容易定义和解决的更小的部分。 这些部件之一是磁性部件。通过整个系统仿真,我们可以轻松定义每个磁性组件端口的匝数比、磁化和漏感、隔离要求,以及重要的电压和电流波形。 使用完整波形 一个要求可能看起来微不足道,但许多工程师在定义变压器时会忽略波形,例如,只使用一些简单的参数(总功率、RMS 值和开关频率),他们认为足以设计磁性元件,但没有意识到它们正在破坏任何可能的优化。 部分原因是许多工程师使用模型或方法来设计初为低频设计的高频磁性元件,并使用面积积方法选择磁芯或仅使用直流值限制电流密度。 完整的波形是摆脱旧方法走向优化的关键。 使用额外信息改进磁性设计 预测磁芯损耗的常用方法是 Steinmetz 方程。该指数方程考虑了开关频率 (f) 和磁通密度 (B)。每种磁芯材料的系数 k、 和 不同,通常由制造商提供(例如 Ferroxcube Steinmetz 系数)。 Pv=k?fα?Bβ
问题在于该方程是在 19 世纪创建的,并假设正弦波形在 21 世纪并不常见。
多年来对该方程进行了许多改进,重要的是改进的广义斯坦梅茨方程(iGSE)。 Pv=1TT∫0ki|dBdt|α( DeltaBβ?α)dt
ki=1(2π)α?12π∫0|cosθ|α2β?αdθ
iGSE 考虑磁通密度波形的完整形状,以极大地改进非正弦工作点的磁芯损耗预测。它将磁通密度波形划分为更小的子环,每个子环具有可能不同的周期和频率。它计算每个子环路的磁芯损耗,将它们相加以获得总磁芯损耗。 更准确的损耗估计反映了对我们选择的的更高信心,因此我们可以在决策中不那么保守并选择较小的,因为知道它不会烧毁。 在任何现代软件中实现这个方程都很简单,但重用经过验证的代码,如图 1 所示。
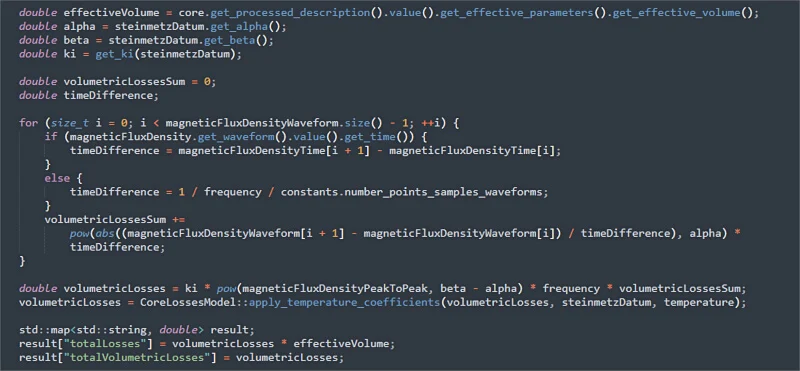
图 1.针对任何给定磁通密度波形的带有 iGSE 实现的 C++ 代码。图片由阿方索·马丁内斯提供 计算出波形的磁芯损耗后,继续使用它们来优化设计,方法是应用快速傅里叶变换 (FFT) 并提取励磁中每个谐波的幅度和频率,以估计绕组损耗。 但在计算它们之前,请确定在绕组中使用哪些电线。从只有低频开关的时代开始,老式方法是将通过电线的电流密度限制在某个保守值(根据我的经验,5-7 A/mm2),并选择符合要求的规格。 更现代的方法考虑趋肤效应,计算开关频率的趋肤深度,并选择半径正好低于该深度的导线,然后根据需要添加尽可能多的平行线,以将直流密度保持在与前一种情况相似的值下。 该方法还包括选择利兹线,其中集肤深度计算线束半径和线束中线束数量的电流密度。还可以在总束中添加平行线,而不是使用许多股线,因为粗线束难以缠绕在线轴中,从而增加了制造成本。 这种方法的问题是它只考虑主谐波的频率,忽略任何较低或较高的频率,并且可能产生两个后果: 如果波形的直流含量很高(如电感器中可能发生的情况),我们终可能会得到一条无法适合绕组窗口的电线,因为较小的股线意味着较小的填充因子值。换句话说,电线越小,用于隔离而不是导电的空间就越大。 如果波形包含许多幅度不可忽略的高频谐波,这些谐波的电流将具有其自身较小的集肤深度。它们的运行电流密度比主要谐波高得多,从而大大增加了绕组损耗。 在这两种情况下,我们终都会得到非设计,要么是因为需要大绕组窗口而使用大磁芯,要么是因为设计具有高绕组损耗。这会增加磁性元件的电线温度,从而增加铜的电阻率,从而产生更多的热量。第二种情况通常终会产生烟雾。 任何选择元件中使用的导线的方法不仅应考虑电流的主要谐波、其直流值或波形的 RMS,而且应考虑电流中的所有谐波(直到给定比例,其中较大的一个为使它们可以忽略不计)。 简单的方法是使用 FFT 并获取电流波形的有效频率。该频率是使用以下公式获得的: feff= ?∞∑j=0I2j?f2j∞∑j=0I2j 其中 Ij 和 fj 是每个谐波的幅度和频率。 该公式由 Charles Sullivan 教授在他的论文“利兹线变压器绕组中股数的选择”附录 C 中介绍,并提供了考虑所有谐波及其幅度的频率。 执行谐波分析并计算有效频率 让我们回顾一下两个有问题的:执行谐波分析和计算有效频率。 对于种情况,与较大的直流偏移相比,我们的电流波形具有相对较小的交流纹波,观察有效频率的值如何远低于开关频率。 如果我们使用图 2 中的情况,开关频率为 100 kHz,有效频率为 9.1 kHz,集肤效应深度约为 0.68 mm。这将导致一根导线的填充因数比开关频率 (100 kHz) 下的导线好得多。该导线对于高次谐波具有较高的集肤效应损耗,但总铜损将随着直流电阻的降低而减少,并且大部分电流为直流电流。
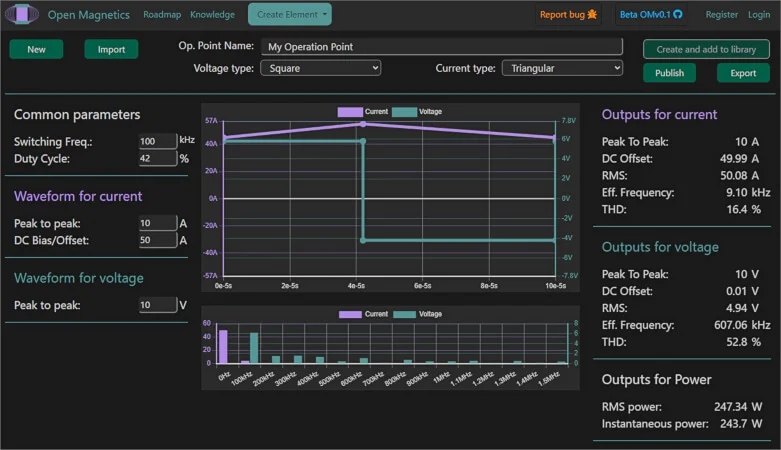
图 2.交流纹波较小的电流波形(上图),因此其傅里叶变换中的谐波很少,并且直流偏移较大(下图)。图片由阿方索·马丁内斯提供 另一方面,第二种情况涉及具有高功率、高频谐波的波形。在这种情况下,有效频率高于开关频率。 以图 3 中的示例为例,开关频率为 100 kHz,有效频率为 623.86 kHz,集肤效应深度约为 0.082 mm。这意味着我们需要一根利兹线,这对于如此高的频率来说是合理的。
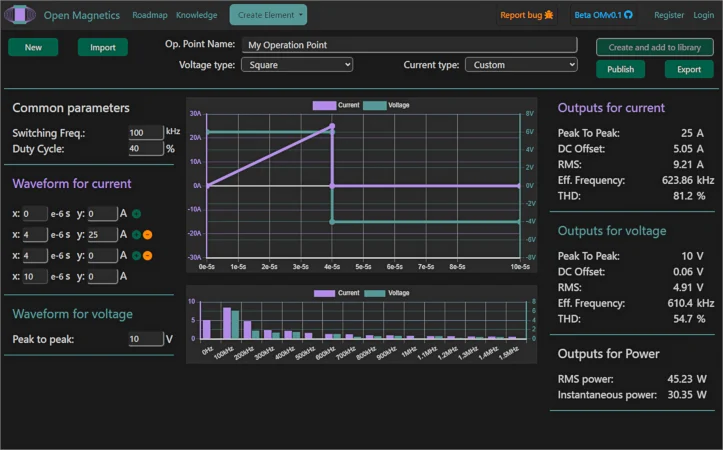
图 3.具有较大交流纹波的电流波形(上图),因此在傅立叶变换中由许多谐波组成(下图),两者均为粉红色,显示在 OpenMagnetics 波形编辑器中。图片由阿方索·马丁内斯提供 该导线将有助于减少高频谐波电流引起的集肤损耗,在低频或直流电流密度与高频电流密度之间找到折衷方案,其中集肤效应大大减少了有用的导电面积在铜中。 在磁学中使用完整波形总结 在设计磁性元件的要求规范中包含完整的波形 有很多好处。我们已经看到,使用它们可以更好地选择磁芯和电线,而不是考虑整个谐波谱,从而实现优化的磁性设计。


