掌握适用于“扭曲”的语义和词汇需要一些训练,但这并不那么令人生畏。你所需要的只是一点耐心来复习相关的代数,而不是乱写乱画。
在讨论
谐波失真时经常遇到两个短语。一是总谐波失真(THD),二是失真因数(DF)。个短语的定义是普遍接受的,但第二个短语的定义通常相当松散,并且没有普遍接受的定义。现在我们来看看失真及其与功率因数的关系(图 1)。
一些作者将 DF 和 THD 视为同义词,但事实并非如此。这两个术语被视为以下 URL 中曾经显示的内容:

(遗憾的是,当我上次查找时,该 URL 已不再起作用。)
图 1功率因数、位移因数和 DF 方程。
在检查功率因数时,如果我们零失真,使得电压和电流都是纯正弦波,则电压和电流波形之间的角差的余弦本身就成为功率因数。然而,我们确实存在波形失真和谐波,因此我们也必须考虑 DF。
现在我们来看看随着 DF 的出现,上述方程如何变化。
首先,我们重申 THD 的定义,然后我们再进行一步,如图 2所示。
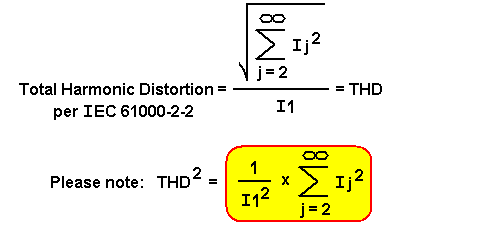
图 2根据 IEC 61000-2-2 定义 THD 及其平方,以便轻松定义图 3 中的 DF。
在我们讨论 DF 时,显示 THD2 的步骤将变得很重要(图 3)。

图 3通过将基波除以全部功率并取其平方根来导出 DF,从而得出 THD 的定义。
传递到负载的功率是基频信号(I12)加上二次谐波信号(I22)加上三次谐波信号(I32)的功率,依此类推,直至驱动波形中存在尽可能多的谐波。
如图 3 的行所示,我们查看基本波提供的功率除以全部功率的比率,并取该比率的平方根,即得出 DF。经过一些代数运算,我们就得到了作为 THD 函数的 DF 方程。


